This lesson investigates a sequence that is defined recursively by examining the graph of the sequence and looking at the associated table of values.

Defining a Recursive Sequence

A recursive sequence defines a term a_n using one or more of the previous terms of the sequence. Because each term is defined using previous terms, the first few terms of the sequence must be defined explicitly.

Explore the recursive sequence shown below that defines each term of the sequence as twice the previous term, a_n = 2a_{n - 1}, and the first term of the sequence is 1.

a_n = 2a_{n - 1}, for n = 2, 3, 4, 5,...

a₁ = 1

Graphing the Recursive Sequence

Define the sequence in the Y= Editor.

• Set u1(n) = 2*u1(n-1)

The function notation u1(n - 1) represents the function value at n - 1. There is no multiplication sign between u1 and (n - 1).

The initial value of the function must also be entered so that the calculator will have a value with which to evaluate the second term. Subsequent terms will be determined by using previously computed terms.

• ui1 = 1

ui1 represents u(1), the first term of the sequence.

• Set the window values to the values below.

nmin = 0	xmin = -1	ymin = -1
nmax = 10	xmax = 10	ymax = 100
plotStrt = 1	xscl = 1	yscl = 10
plotStep = 1

• Display the graph of the sequence

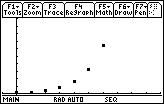
The graph suggests that the sequence gets large without bound as n approaches and therefore diverges.

Creating a Table of Values

The divergence of the sequence can by supported by viewing a Table of values.

• Set tblStart = 1 and tbl = 1 in the Table Setup dialog box
• Display the Table

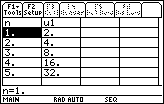
It appears from the table that this sequence is the sequence a_n = 2ⁿ. The sequence a_n = 2ⁿ is called the geometric sequence and it is divergent.

Defining a Recursive Sequence Requiring Two Previous Values

In the sequence investigated above, each term was defined as twice the value of the preceding term. Recursive sequences can also be defined using more than one preceding term.

Explore the recursive sequence that defines each term as the sum of the two previous terms where the first two terms are 1 and 1.

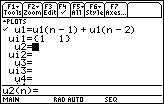
• Set u1(n)=u1(n-1)+u1(n-2)
• Set ui1 = {1,1}

The initial value ui1 is the list {1,1}, which represents the values of the first two terms.

The symbols '{' and '}' are found above the parentheses.

• Set tblStart = 0 and tbl = 1

21.3.1 Display the table and identify the sequence shown.
Click here for the answer.