![]()
As n gets larger subsequent terms in the sequence get closer to zero.
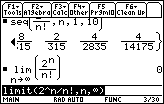
The limit of the sequence as n approaches
![]() is 0.
is 0.
A table of values of the terms of the sequence gives numerical evidence that the sequence converges.
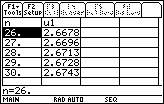
The value of
![]() gives analytical proof that the sequence converges.
gives analytical proof that the sequence converges.
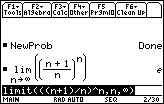
The sequence converges to e
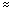 2.71828.
2.71828.
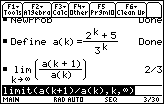
Because the limit of the ratio of the sequence of partial sums is less than 1, the series converges.
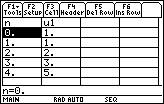
The sequence is known as the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34,...
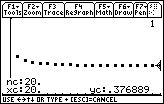
The sequence appears to converge to approximately 0.377. The actual value is
![]()
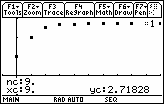
The series appears to converge to approximately 2.71828. The exact value is
![]()
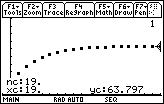
The sequence appears to converge to approximately 63.797. The exact value is 64.
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy