In Lesson 8.1 and Lesson 8.2 of this module you investigated the derivative of a function at a single point, which was defined to be the slope of the line tangent at that point. In this lesson you will download and use a program named tanimate to visualize derivatives at several sequential points along a curve. This will help to illustrate the concept of the derivative of a function as a function.

The TI-89 program called tanimate displays an animated sequence of tangent lines for a given function. It also plots points representing the slopes of those tangent lines. John Hanna, who is a teacher at Teaneck High School, New Jersey, wrote this program for the TI-89. Before you can use this program, you will need to complete the following steps to install the program on your TI-89 calculator.

Downloading the Program to Your Computer

• Click here to download tanimate to your computer
• Choose to save the file
• Save the file on your local hard disk in a folder that you can access later

Transferring the Program to the TI-89

Click here to get information about how to obtain the needed cable and to review the procedure to transfer the program from your computer to your calculator.

• Send the tanimate program from your computer to your TI-89

Animating Tangent Lines

The program tanimate requires that you store the desired function into y1 in the Y= Editor and then display its graph.

• Graph y1 = x² in a [-4, 4] x [-4, 4] window
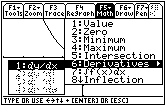
• Press and select 1:dy/dx.
  Compute the derivative at x = -2, -1, 0, 1, 2. Click here for the answers.
 

You could find the derivative at many more points as well. These points could then be plotted as a scatter plot. However, this is tedious, so let's use "tanimate" to automate this process.

• Return to the Home screen

Running tanimate

• Select tanimate by pressing and scrolling down until it is highlighted

• Paste "tanimate(" to the Edit Line by pressing
• Enter the closing parenthesis by pressing

• Run the program by pressing

The function y = x² will be graphed again and the program's Main Menu dialog box should appear.

• Display the "Choose" options by pressing
• Highlight "2:Animated" by pressing

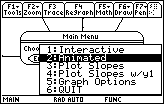
• Select this choice by pressing
• Move to the next dialog box by pressing again

The next dialog box is used to set the sampling rate, which determines the number of points that will be used to create and display the tangent lines.

• Display the Sampling Rate menu by pressing
• Highlight MEDIUM

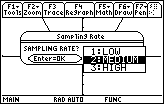
• Select this choice by pressing
• Display the next dialog box by pressing

Now you should see the Display Menu dialog box.

• Open the Options menu by pressing
• Highlight "TANGENT&PTS" by pressing

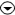
• Save your selection and proceed by pressing twice

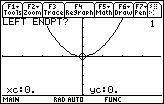
Setting the Left Endpoint

Now you should see the graph and a prompt for the left endpoint. Tangent lines will be drawn beginning with the x-value that you set as the left endpoint, and this value must be within the current window's coordinates.

• Enter -2 by pressing

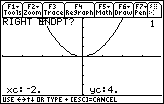
Setting the Right Endpoint

Next you should see a prompt for the right endpoint. This value determines the x-value of the last tangent line that will be drawn. Again, this value must be within the current window's coordinates.

• Enter 2 by pressing
• Watch the program run

Viewing Animated Tangent Lines and Plotted Slopes

You should see an animation of tangent lines. As each tangent line is graphed, a corresponding point is plotted. The x-coordinate of the plotted point is equal to the x-coordinate of the point of tangency, and the y-coordinate of the plotted point is the slope of the corresponding tangent line.

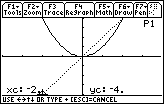
The screen shows the graph at the end of the program.

Finding Derivatives at Several Points

The tanimate program can display the value of the derivative (slope of the tangent line) at specific points.

• Display the values of the derivative at several points by pressing and noting the x- and y-values at the bottom of the screen

The derivative of f(x) = x² at x = -0.9 is -1.8, as shown by the coordinates at the bottom of the screen below.

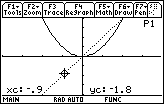
8.3.2 Find the derivative when x = 1.2 and interpret its value. Click here for the answer.

Exiting the Program

• Return to the program's Main Menu by pressing
• Exit the program by selecting "6:Quit" and pressing

The Derivative as a Function

The set of points plotted by tanimate represents the slopes of the tangent lines. These points represent a function whose y-values give the derivatives of the function at each point. Notice that the points on the graph of the derivative of f(x) = x² appear to lie on a line. The derivative of f(x) = x² is the linear function represented by the line that connects these points.

You can use the derivative key to find the symbolic representation for the derivative function. The syntax for finding the derivative function is similar to the one for finding the value of the derivative at a point, but the "with" command that establishes the variable's value is omitted.

• Enter d(x^2,x) into the Edit Line
• Find the expression that represents the derivative by pressing

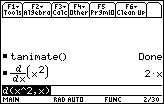
The derivative of f(x) = x² is the function f'(x) = 2x.

8.3.3 Illustrate the derivative of f(x) = 3x² + 4x using the tanimate program and then use the d( command to find derivative function. Click here for the answer.