Module 8 - Derivative of a Function

Module 8 - Answers

Lesson 1

Answer 1

8.1.1 The slopes of the secant lines appear to converge to 1, so the slope of the tangent line is probably 1.

Answer 2

8.1.2 Approximately [-2.12, 4.12] x [-1, 2].

Lesson 2

Answer 1

8.2.1 The function

is not differentiable at x = 0 because it is not locally linear there. The function

is differentiable at x = 0 because it is locally linear there.

Lesson 3

Answer 1

8.3.1 x = -2: dy/dx = -4; x = -1: dy/dx = -2; x = 0: dy/dx = 0; x = 1: dy/dx = 2; x = 2: dy/dx = 4

Answer 2

8.3.2 The derivative is 2.4, which represents the slope of the tangent line to f(x) = x² at x = 1.2.

Answer 3

8.3.2

The derivative of f(x) = 3x² + 4x is the function g(x) = 6x + 4.

Self Test

Answer 1

Answer 2

Answer 3

Answer 4

Answer 5

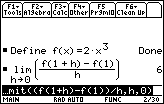
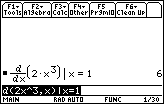
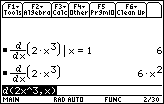
The tangent line is y = 6(x – 1) + 2, which is shown with the function in a [–3, 3.32] x [–10, 10] window.

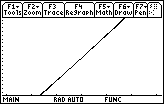
The graph is shown after zooming in three times centered on (1, 2) with zoom factors xFact = yFact = 10.