In Module 7 you saw that velocities correspond to slopes. Average velocity corresponds to the slope of a

A secant line is a line through two points on the curve.

secant line that connects two points, and instantaneous velocity corresponds to the slope of a line tangent to the curve. The derivative of a function at a point is the slope of the tangent line at that point. In this lesson you will use several different features of the TI-89 to find derivatives.

Formal Definition of Derivative

The derivative of a function f at x = a is

provided the limit exists. The secant lines converge to a tangent line if one point on the curve is fixed and the second point approaches that fixed point.

Illustrating Secant Line Convergence

The following procedure will find the value of the derivative of the function f(x) = 2x – x² at the point (0.5, 0.75) by using a method similar to the one you used to find instantaneous velocities. First, you will find the slopes of several secant lines and use them to estimate the slope of the tangent line at x = 0.5. Then you wil take the limit of the slopes of the secant line to find the derivative.

The graph below illustrates f(x) = 2x – x² in the window [-1, 3] x [-1, 2], with the three secant lines that approximate to the tangent line at (0.5, 0.75).

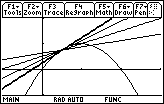
Finding Slopes of Secant Lines

• From the Home screen, select NewProb from the F6:Clean Up menu
• Define f(x) = 2x – x²

The slope of the secant line through the points (0.5, f(0.5)) and (0.5 + h, f(0.5 + h)) can be found by evaluating the difference quotient

We're interested in values of h which are small so that the two points are close together and the resulting secant line will aproximate the tangent line.

• Evaluate this difference quotient for h = 0.1 using the "with" command by entering
  (f(0.5+h)-f(0.5))/h | h=0.1. The "with" command (vertical bar) is to the left of the key.

The slope of the secant line containing (0.5, f(0.5)) and (0.6, f(0.6)) is 0.9.

Using Smaller Values of h

As the point (0.5 + h, f(0.5 + h)) approaches the point (0.5, f(0.5)), h approaches 0 and the secant lines converge to the tangent line.

Evaluate the difference quotient for smaller values of h.

• Change the value of h in the Edit Line from 0.1 to 0.01 and evaluate the difference quotient

The slope of the corresponding secant line is 0.99.

• Evaluate the difference quotient with h = 0.001 and with h = 0.0001

The slopes of the secant lines are 0.999 and 0.9999, respectively.

8.1.1 Predict the slope of the tangent line at (0.5, f(0.5)). Click here for the answer.

• Evaluate the difference quotient with h = -0.01 and h = -0.001


The slopes of the corresponding secant lines are 1.01 and 1.001. One secant line passes through (0.499, f(0.499)) and (0.5, f(0.5)), the other through (0.4999, f(0.4999)) and
(0.5, f(0.5)).

• Next compute the difference quotient without specifying a value for h.


Notice that we get a formula for the difference quotient when no value is specified for h.

Finding a Derivative at a Point

The derivative, which is the slope of the tangent line, is defined to be the limit

• Evaluate this expression by entering the command limit((f(0.5+h)-f(0.5))/h,h,0)

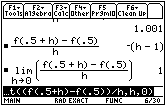
The derivative of f(x) = 2x – x² at x = 0.5 is 1.

Using the Derivative Command

You can also evaluate the derivative of the function f at x = 0.5 by using the derivative command d(, which is found above the key and also in the Calc menu. The syntax for finding a derivative at a point is d(expression,variable) | variable=value.

• Paste d( to the Edit Line by pressing [d]
• Compute the derivative of f at the point with x = 0.5 by entering the expression d(f(x),x)|x=0.5

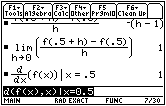
Drawing the Tangent Line

Now that the point on the curve and the derivative at that point are both known, the

The equation of the line through the point (x1, y1) with slope m is y – y1 = m(x – x1).

point-slope form for the equation of a line can be used to find an equation for the tangent line. If the slope of the tangent line at (0.5, 0.75) is equal to 1, then the equation for the tangent line is y = 1·(x – 0.5) + 0.75.

Graph the function f and its tangent line at (0.5, 0.75).

• Set y1 = f(x)
• Set y2 = (x–0.5) + 0.75
• Graph both the function and the tangent line in a [-1, 3] x [-1, 2] window with xscl and yscl = 1

The line appears to be tangent to the curve at x = 0.5.

Using a Square Window

It sometimes helps to visualize the value of the slope of the tangent line by drawing the graph in a square viewing window, where a unit on the x-axis is the same width as a unit on the y-axis.

• Display the graphs in a square viewing window by pressing F2:Zoom and selecting 5:ZoomSqr

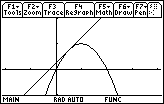
In this window, the slope of the tangent line appears to be 1.

8.1.2 What are the coordinates of the viewing window above? Click here for the answer.