The TI-89 computer algebra system has a limit function. In this lesson you will use the TI-89 computer algebra system to find limits.

Using the Limit Function

From the Home screen, evaluate by using the limit( command.

• Display the Calc menu by pressing

• Paste the limit( command to the Edit Line by pressing
• Enter the function by pressing
• Complete and execute the command by pressing

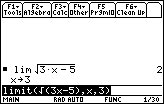
So, .

4.3.1 Use the limit( command to evaluate . "Sin" is a yellow feature above the key and is a green feature above the key. Be sure the calculator is in radian mode. Click here for the answer.

4.3.2 is 1 in Radian mode. Find in Degree mode. Click here for the answer.

The Angle mode makes a difference in the evaluation of . Most angle calculations in Calculus are done in Radian mode, so switch back to Radians now.

The Sandwich Theorem

The Sandwich Theorem is used in many Calculus books to prove = 1. It can be shown that cos < < 1 , and because the left and right terms in the inequality approach 1 as 0, it must follow that the middle term also approaches 1.

This theorem can be visualized by graphing the three terms in the inequality simultaneously.

• Enter the three functions shown in the Y= menu below

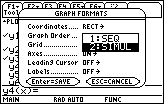
The graph format needs to be changed to simultaneous.

• From the Y= Editor display the Tools menu by pressing
• Highlight "Format" by using the cursor movement keys

• Open the Format submenu by pressing
• Display the Graph Order options by pressing
• Select "SIMUL" by pressing and

• Save the Graph Format changes by pressing
• Display graphs of the functions in a [-3, 3] x [-1, 2] window

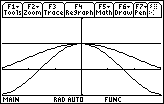
Seeing the three graphs simultaneously converge to 1 around x = 0 illustrates the Sandwich Theorem argument that = 1. You can see the three functions converge again by pressing the Regraph button .

Left- and Right-Hand Limits

The limit( command can also be used to evaluate a left-hand limit or a right-hand limit, which is the value approached by a function as x approaches a specific value from the left or from the right.

4.3.3 Interpret and evaluate it with the command limit(1/x,x,0,-1). Click here for the answer.

4.3.4 Interpret and evaluate it by changing –1 to 1 in the Edit Line. Click here for the answer.

Using the Trace Feature

The Trace feature may be used to estimate limits. As the Trace cursor moves along a curve, the x- and y-values appear at the bottom of the Graph screen. Look at the y-values of y = as x approaches 0 from the left and from the right by using the Trace feature.

• Graph y = 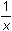in a [-3, 3] x [-10, 10] window
• Activate the Trace cursor by pressing
• Display coordinates of the graph by repeatedly pressing or to move the cursor along the curve

Moving the Trace cursor toward zero from the left or the right provides dynamic graphical and numeric reinforcement for the left- and right-hand limits.

Entering a Specific x-Value

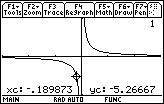
While the Trace cursor is active, you can move it to a particular point by typing in the x-coordinate of that point. For example, to move to the point with x = –0.001,

• Enter –0.001.

This value should appear by "xc" in the lower left corner of the screen.

• Execute the command by pressing

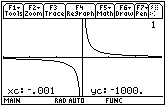
The cursor is not visible since it is below the viewing window, but the coordinates of the cursor are shown giving further evidence that .