In the previous lesson you found tolerances graphically. In this lesson you will use the TI-89 computer algebra system to find these tolerances symbolically. This will prepare you to generalize the tolerances and develop the definition of limit.

Tolerances

The first tolerance you found in lesson 4.1 was in response to the question

How close should x be to 3 so that is within 0.1 of 2?

Restate the Question

Another way to phrase this question is

Find a positive number so that 1.9 < < 2.1 whenever 3 – < x < 3 + .

Given y-Tolerance, Find x-Tolerance

The x-tolerance when the y-tolerance is 0.1 can be found by solving the

A compound (or extended) inequality is an inequality that compares more than two quantities and contains more than one inequality symbol.

compound inequality 1.9 < < 2.1. To find the values, use the solve( command to find the solutions to 1.9 = and = 2.1. Press or set the mode to AUTO.

The solution is approximately 2.87 < x < 3.13667.

Notice that the solutions are the same as those found in Lesson 4.1 when you used the intersection feature.

Finding

Compare 2.87 < x < 3.13667 with the inequality 3 – < x < 3 + . It must follow that 3 – 2.87 and 3 + 3.13667 . However, solving these two equations for yields two different values: 0.13 and 0.13667. As in lesson 4.1, the smaller of the two values is the correct answer: 0.13.

Smaller Tolerance

The second tolerance you found in lesson 4.1 came from answering the question

How close should x be to 3 so that is within 0.01 of 2?

4.2.1 Rephrase this question with compound inequalities. Click here for the answer.

4.2.2 Use the solve( command to solve the first compound inequality. Click here for the answer.

4.2.3 Compare your answer to 4.2.2 with the inequality 3 – < x < 3 + and find a value of , the x-tolerance. Click here for the answer.

Finding a Generalized Solution

Suppose that you are asked to find values of that correspond to smaller and smaller tolerances for y around y = 3. Rather than going through the same process over and over for various y-tolerances, you could solve the problem once with a generalized y-tolerance. Call this general y-tolerance , the Greek letter "epsilon." The Greek letters delta, , and epsilon, , will be used to represent small positive numbers.

The tolerance question then becomes

How close should x be to 3 so that is within of 2?

Rephrasing the Question

The question can be rephrased using inequalities as

Find a positive number so that 2 – < < 2 + whenever 3 – < x < 3 +

Solving the Left Inequality: 2 – <

• Solve the left side of the inequality 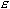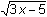2 – < < 2 + 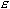with the command
solve(2- = (3x–5),x)

The Greek letter can be entered in the TI-89 by pressing .

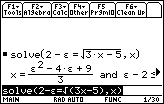
The solution to the equation has two parts:

and – 2 0.

The second part of the solution, – 2 0, is always true because is a small positive number.

Entering Greek Letters Greek letters are entered on the TI-89 by first pressing and then entering the corresponding alpha key. For example, the Greek letter (Delta) is entered by pressing . The alpha character above is [D], which corresponds to .

Solving the Right Inequality: < 2 +

You can edit the command shown in the Edit Line to solve the right inequality by changing the "–" sign to "+."

• Edit the expression on the Edit Line to read solve(2+ 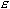= (3x–5),x) by using the cursor movement keys and
• Execute the command by pressing

The solution is and – 2.

Because is a small positive number, the statement – 2 is always true.

Combining the solutions to find

Combining the two solutions, in order to have 2 – < < 2 + we need

Comparing this inequality with 3 – < x < 3 + yields

  and  

Solving these equations

for gives and

The smaller of these two values is , which is the general solution. Given any value for you can use this equation to find the corresponding value for . For example, when = 0.01, this equation gives = 0.0133, the same value we found earlier.

Limits

When the values of the output can be made as close as we like to 2 by taking input values sufficiently close to 3, we say

The limit of the function f(x) = as x approaches 3 is equal to 2.

That is, the value of f(x) = gets closer and closer to 2 as x gets closer and closer to 3. The notation used to indicate this is

which is read "the limit of as x approaches 3 is 2."

In the previous example we found that guarantees that

2 – < < 2 + whenever 3 – < x < 3 + .

Because for any positive , a corresponding positive can be found that meets the conditions above,

Definition of Limit

Formally, if for any > 0, however small, there exists a > 0 such that

L – < f(x) < L + whenever a – < x < a +

Conceptually, f(x) L as x a.

4.2.4 Write the inequality with conditions that is associated with the limit. Interpret .

Click here for the answer.