-
Graph
y1 =
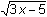
y2 = 2 – 0.01 = 1.99
y3 = 2 + 0.01 = 2.01
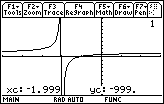
- Set the viewing window to [2.98, 3.02] x [1.98, 2.02]
- Find the intersection points by using the Intersect command
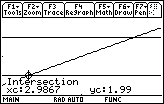
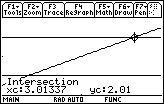
Use the intersection points to find the tolerance for x that produces a y-tolerance of 0.01.
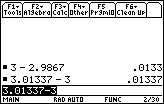
Choose the smaller of the two tolerances. The y-tolerance is 0.01 when the x-tolerance is 0.0133.
Solve 3 –
![]()
![]() 2.9867 and 3 +
2.9867 and 3 +
![]()
![]() 3.01337 for
3.01337 for
![]() to obtain
to obtain
![]()
![]() 0.0133 and
0.0133 and
![]()
![]() 0.01337.
0.01337.
The correct tolerance is the minimum of the two values,
![]()
![]() 0.0133.
0.0133.
![]() means that
means that
![]()
![]() 5 as x
5 as x
![]() 10.
10.
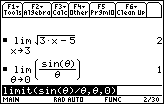
![]() = 1
= 1
-
Display the mode settings dialog box by pressing
-
Select Angle's setting by pressing
 three times
three times
-
Open the Angle submenu by pressing

-
Highlight "Degree" by pressing
-
Select "Degree" by pressing

-
Save the changes and exit the Mode screen by press

The fourth item in the menu is the Angle mode.

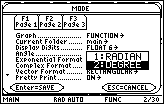
The mode settings under the Edit Line should say DEG to indicate the calculator is currently in Degree mode.
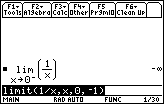
The limit function should still be on the Edit Line.
-
Execute it again by pressing

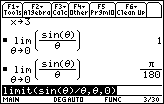
![]()
which is interpreted as
![]() when x
when x
![]() 0 from the left.
0 from the left.
![]() represents the value that
represents the value that
![]() approaches as x approaches 0 from the right.
approaches as x approaches 0 from the right.
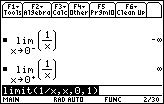
![]() =
=
![]()
which is interpreted as
![]() when x
when x
![]() 0 from the right.
0 from the right.
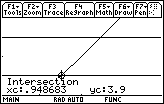
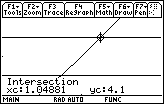
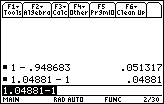
x should be within approximately 0.04881 of 1
Find a positive number
![]() so that 3.9 < x2 + 3 < 4.1 whenever 1 –
so that 3.9 < x2 + 3 < 4.1 whenever 1 –
![]() < x < 1 +
< x < 1 +
![]()
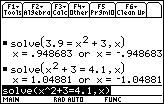
Because x is near 1, the positive solutions are what we need. Therefore,
1 –
![]() = 0.948683 and 1 +
= 0.948683 and 1 +
![]() = 1.04881.
= 1.04881.
Solve for
![]()

Taking the minimum of the two values, x should be within approximately 0.04881 of 1.
- 4
- 3
-
–
-
©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy