In this lesson you will explore an application that is modeled using exponential decay. The model used is similar to the one explored in Lesson 21.1.

Newton's Law of Cooling

Sir Isaac Newton (1642-1716) discovered how a hot liquid cools to the temperature of its surroundings. The form of the equation that models the cooling situation is a modification of the differential equation explored in Lesson 21.1. In that lesson, the rate of change of the balance in the account was directly proportional to the balance at any time t:

.

The differential equation that describes how a liquid cools has a similar form. To write the equation for the cooling problem, we need the following variables.

L = Temperature of the liquid at time t S = Temperature of the surroundings Y = L - S (The difference between the temperature of the liquid and the surroundings.) t = Time B = Initial (beginning) temperature of the liquid (Temperature at t = 0) k = Cooling constant

Newton's Law of Cooling describes the change in the liquid's temperature. It says that the rate of cooling of a liquid is proportional to the temperature difference between the liquid and its surroundings. That is,

where k is the constant of proportionality and represents the rate at which the difference between the liquid and the surrounding temperature is changing. The negative sign in front of k indicates that the temperature difference, Y, is decreasing.

The Temperature Equation

An equation that gives the temperature of the liquid at time t can be found by solving the differential equation given above with the initial condition that the temperature difference at t = 0 is Y₀ = I - S. The solution has the form

Substituting Y = L - S and Y₀ = B - S the equation can be solved for L. The result is an equation that gives the temperature of the liquid at time t.

Specific Solutions

If the required data is available, here is one way that the model can be used.

1. Write the equation for the model: L = (B - S)e^{-k · t} + S.
2. If the initial temperature of the liquid (B), the temperature of the surroundings (S), and the temperature of the liquid (L) at a second time (t) are all known, find the value of k by substituting those 4 values into the equation and solving for k.
3. Using the value of k found, the equation that gives the liquid's temperature can be used to find other values.

A Cooling Example

Suppose a cup of water was heated to a temperature of 65°C and placed in a refrigerator that had a temperature of 5°C. The water cooled to a temperature of 11°C in 30 minutes. Find the temperature of the water after 60 minutes.

The equation for the model is L = (B - S)e^{-k · t} + S.

The Equation Solver can be used to find specific values for k and then for L, but the equation must first be changed to a form that has zero on one side of the equation. Subtracting the terms on the right side of the equation gives

Enter the equation in the Equation Solver.

• Open the Equation Solver from the MATH menu.
• Clear the old equation by pressing to move the cursor to the equation and then pressing .
• Enter the expression L - (B - S)e^{-k · t} - S.
  
  
• Press to enter the equation and open the Solver menu.

Find the value of k by using the condition L = 11 when T = 30.

• Enter the following values:
  L = 11 (Temp. of liquid)
  B = 65 (Initial temp.)
  S = 5 (Surrounding temp.)
  K = 1 (An arbitrary initial guess)
  T = 30 (Time, in minutes)
  
• Move the cursor beside "K" and press  [SOLVE].
  
  

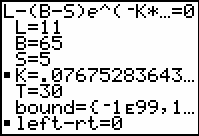
The value of k, the constant of proportionality, is approximately 0.0768.

You can now determine the temperature of the liquid after 60 minutes by simply changing the value for time and solving for L.

• Change the value of "T" to 60.
• Move the cursor beside "L" and press  [SOLVE].
  
  

After 60 minutes the water will be about 5.6°C.

21.2.1 A cup of water was heated to a temperature of 70°C and placed in a refrigerator that had a temperature of 8°C. The water cooled to a temperature of 14°C in 30 minutes. Find the temperature of the water after 60 minutes.

Click here for the answer.