In this lesson you will explore the first of three applications where the change in an amount is directly proportional to the amount present. The first type of application is continuously compounded interest, which is represented by an exponential growth model.
Modeling Continuous Compound Interest
When interest on an account is compounded continuously, the account grows at a rate that is directly proportional to the size of the account. In other words the larger the account, the faster it grows. This can be described by the differential equation
where A is the balance in the account after t years and r is the annual interest rate in decimal form. The first derivative of A with respect to time,
,
represents the rate at which A is changing.
Continuously Compounded Interest
The equation for the balance in the account can be found by solving the initial value problem
and A(0) = p.
The constant of proportionality is r, and it is called the continuous growth rate as long as it is positive. The initial condition indicates that the initial balance at time 0 is p.
Solving the Differential Equation
Separating the variables in the equation
gives
.
Both sides of this equation can be integrated to get the solution to the differential equation
.
The result of the integration is
Solving this equation for A and using properties of exponents gives
The value of C0 can be determined by substituting the initial condition that A = p when t = 0 into the last equation.
or
C0 = p
Therefore, the amount in the account after t years is given by
where p is the original amount in the account and r is the interest rate. This equation can be used to determine specific values.
Doubling Time
Suppose $1000 is deposited into an account that pays interest compounded continuously at an annual rate of 6.5%. You can find how long it will take to double the amount in the account by using the equation.
Equation Solver
The doubling problem is easily solved using the Equation Solver feature of the TI-83. The Solver feature can return an approximation of a solution to an equation, if such a solution exists.
First, enter the equation in the Equation Solver.
-
Press
to open the MATH menu.
-
Select 0:Solver from the MATH menu.
-
If there is an existing equation in the Solver, press
to move the cursor up to the equation and
to clear the equation.
Equation Solver will only accept equations that have zero on the left-hand side, so rewrite the equation as
- Enter the equation A - Pe^(R*T).
-
Press
to store the equation and open the Solver menu.
You should see the variables A, P, R and T, which are the variables from the equation. Because P = 1000 and you want to find the time it will take for the amount to double, set A = 2000. The value of R is 0.065. You should enter an initial guess for T. Try T = 5.
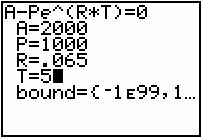
Solve for T
- Make sure the cursor is beside "T", then press
[SOLVE]. [SOLVE] is above
.
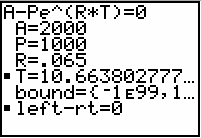
The number shown next to T is the solution. The account will double in about 10.7 years.
21.1.1 Find the doubling time for the investment if the initial amount is p = 7,000. Find the doubling time if p = 25,000. What if p = 50,000? Make a conjecture based on your results.
Click here for the answer.
 |
|||
|
|||
|
|||
Other Compound Interest Problems
Suppose $1000 is deposited into an account that pays interest compounded continuously at an annual rate of 7%.
21.1.2 Solve the initial-condition problem
, A(0) = 1000.
Click here for the answer.
21.1.3 Determine how much the account will be worth in 30 years.
Click here for the answer.
21.1.4 How much will an initial investment of $5,000 be worth in 35 years if it earns interest compounded continuously at an annual rate of 8.5%?
Click here for the answer.
21.1.5 You deposit $7500 at 4.5%. How long does it take for the account to have a balance of $10,000?
Click here for the answer.