The following questions illustrate the procedure used to find the rectangle inscribed under the graph of f(x) = sin x in the first quadrant on the interval [0, ] that has maximum area. Here x stands for the x-coordinate of the lower left corner of the rectangle. The area of a rectangle is A = hw, where h and w are the height and width of the rectangle, respectively.

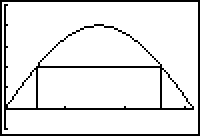
1. Define the height as a function of x.
2. Define the width as a function of x. (Hint: Use the symmetry of the rectangle's base in the interval [0, ].)
3. Enter the height, width and area functions in Y₁, Y₂ and Y₃ of the Y= editor of your TI-83. Unselect Y₁ and Y₂.
4. Define the derivative of the area function in Y₄.
5. Graph the area function and its derivative. Describe the correspondence between the derivative and the maximum of the function.
6. Find the zeros of the derivative on the interval .
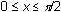7. Verify that the critical point found in Question 5 produces the absolute maximum of the area function and find the maximum area of the rectangle.

Click here to check your answers.