In Lesson 14.2 you investigated when the surface area of a can was minimized. In this lesson you will explore the more realistic problem of finding when the amount of material used in making the can is minimized.

The Problem

A can is made from a rectangular piece that forms the lateral surface and two circles cut from square pieces that form the top and bottom. The volume of the can is to be 255 cubic centimeters. The following discussion will find the radius of the can and the ratio of height to radius when the amount of material used is minimized.

The Diagrams

The diagrams below illustrate a can of height h and radius r with the top and bottom cut from square pieces of material.

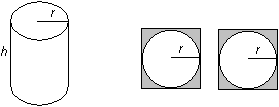
Although the shaded area is not part of the can, it must be included in the material used.

Material Used as a Function of Radius and Height

The amount of material used is the sum of the areas of the two squares that are used to create the top and bottom and the rectangle that is used for the lateral area. The length of the sides of the squares is 2r and the rectangle's sides are 2 r and h, so the material used to create the can is given by:

M = 2(2r)² + 2 rh
= 8r² + 2 rh

Radius and Height as Functions of x

The material used is a function of two variables, r and h. The variables r and h should both be defined in terms of x so that the material function can be written as a function of one variable.

The desired volume is 255 cubic centimeters and the formula for volume is V = r²h. Therefore, 255 = r²h.

Solving the equation for h gives

Letting r = x, r and h can both be defined as functions of x.

r(x) = x

h(x)=255/( *(r(x))²)

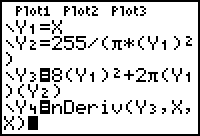
These functions can be entered in the Y= menu. Define r(x) in Y₁ and h(x) in Y₂, letting Y₁ represent r.

• Enter Y₁ = X.
• Enter Y₂ = 255 / ( * (Y₁) ² ).
• Unselect Y₁ and Y₂.

Recall that the function that represents the material used is M = 8r² + 2 rh. Define the function for the material used in Y₃ letting Y₁ represent r and Y₂ represent h.

• Enter Y₃ = 8(Y₁)² + 2 (Y₁)(Y₂).

The Derivative of Material used with Respect to x

Store the derivative of the material used in Y₄.

• Enter Y4 = nDeriv(Y₃,X,X).

The Zero(s) of the Derivative

The domain of the material used function is x > 0. As before, experiment with different viewing windows to better understand the graphs of the function and its derivative. You will see that the derivative appears to only have one zero. Find the approximate value of the zero of the derivative.

• Display the graphs of the material used and its derivative in a [0, 7, 1] x [-200, 400, 50] window.
• Use the Zero feature to find the zero of the derivative.

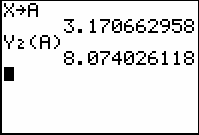
The critical point is x 3.1707, which represents the radius of the can. It is good practice to store all the decimals found for x in the above figure before calculating the colrresponding height. The figure below shows the value found for x stored into A and the corresponding height computed. The corresponding height is approximately 8.0740, which is found by evaluating Y₂(A).

Accuracy It is a good idea to always store any intermediate values in the calculator so they can be used later to the full accuracy the calculator allows. Rounding versions of intermediate results and then using them to compute further results leads to errors being compounded.

Other Possible Extreme Values

The first derivative is defined everywhere in the function's domain, so x 3.1707 is the only critical point. There are no endpoints to consider. We can pin these facts down by finding an analytic formula for the function and its derivative. We could also use their graphs to support this information.

The Second Derivative

We can also use the second derivative test to check the information found above. Test the critical point in the second derivative of the material used to justify that it represents a local minimum.

• Enter nDeriv( Y₄, X, 3.1707) on the Home screen.

Because the second derivative of the material used is positive at x 3.1707, the graph of the function is concave upward and has a local minimum value there.

Because there are no endpoints and no other critical points, the local minimum value is the absolute minimum value.

The Ratio of Height to Radius

Evaluate the ratio of height to radius, , at the zero of the derivative.

• Enter the command Y₂(3.1707) / Y₁(3.1707) on the Home screen.

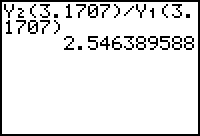
The ratio of height to radius for the can with minimum material used appears to be approximately 2.5464. We can improve this approximation by using all the decimals that the calculator finds for the zero of the derivative.

14.3.1 Change the volume of the can to 355 cubic centimeters. Find the zero of the derivative of the material used function for the new can and find the ratio of height to radius at that point. Compare the ratio of height to radius of the can that holds 355 cubic centimeters to that of the can that holds 255 cubic centimeters.

Click here for the answer.

The Generalized Can With Waste Problem

It can be proven that the ratio of height to radius for the can in this lesson is for any fixed volume.