• Define the second derivative of the volume function (Y₃) by finding the derivative of the first derivative of the volume function (Y₄). This is done by entering Y₅ = nDeriv( Y₄,X,X).
• Find the value of the second derivative at the critical point by entering Y₅(1.15299) on the Home screen.

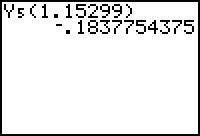
Because the second derivative is negative at the critical point x = 1.15299, the function has a local maximum there.

Change Y₂ to 355 / ( * (Y1) ² ) , unselect Y₂ and graph the surface area function and its first derivative. The new zero of the derivative is x 3.8372. The ratio of height to radius is still approximately 2.

The height is h = sin(x).

Since the rectangle is symmetric about x = /2, the width is .

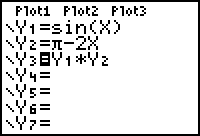
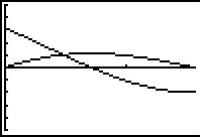
Because the derivative is positive to the left of x 0.7105 and negative to the right of x 0.7105, there is a maximum of the area function at x 0.7105. The graphs are shown above in [0, /2,1] x [-5,5,1] .

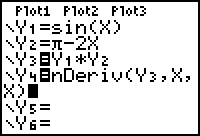
The zero of the derivative on the interval .

From the graph it appears that the derivative is defined on the entire interval. The end points produce an area of 0 and x 0 .7105 is the only critical point. The area of the rectangle at this critical point is approximately 1.1222 square units. The value of the second derivative at this critical point is about -4.1544. As a check, notice that the second derivative is negative, so the critical point produces a maximum. Since this is the only critical point, it produces an absolute maximum.