In Lesson 14.1 the length of a removed arc that maximized the volume of a cone was found. In this lesson the radius of a can that minimizes surface area will be explored.

The Problem

A

A circular cylinder is a solid that consists of circular bases which are parallel to each other in 3-space. If the axis of the cylinder is perpendicular to the bases, then the circular cylinder is called a right circular cylinder.

right circular cylindrical can is being designed to hold 255 cubic centimeters. The following discussion will find the dimensions of the can with the least surface area and then find the minimum surface area.

The diagram below illustrates a can of radius r and height h.

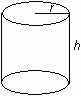
Surface Area as a Function of Radius and Height

The surface area includes the lateral surface (the side of the can) and two circles that form the top and the bottom. The lateral surface, if "unwrapped" and laid flat, forms a rectangle with height h and width equal to the circumference of the can. Therefore, the surface area is the sum of the areas of the two circles and the rectangle:

S = 2 r² + 2 rh

Radius and Height as Functions of x

The surface area is a function of two variables, r and h. If r and h are both defined in terms of a single variable x, then the surface area will be defined as a function of x, which will allow us to use the techniques we have discussed to solve the problem.

The desired volume is 255 cubic centimeters and the formula for the volume of the can is

V = r²h

Therefore, 255= r²h.

Solving the equation for h gives

Letting x represent the radius of the can, the radius and the height can both be defined as functions of x.

r(x)=x

h(x)=255/ *(r(x))²)

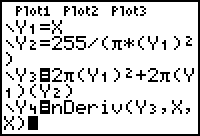
These functions can be entered in the Y= editor.

• Enter the radius as Y₁ = X.
• Enter the height as Y₂ = 255 / ( * (Y₁)² ).
• Unselect Y₁ and Y₂.

Recall that the formula for surface area is

S = 2 r² + 2 rh

Define surface area in Y₃ by letting Y₁ represent r and Y₂ represent h.

• Enter Y₃ = 2 (Y₁)² + 2 (Y₁)(Y₂)

Now surface area is defined as a function of x and stored in Y₃.

Finding the Derivative of Surface Area with Respect to x

Store the derivative of the surface area in Y₄.

• Enter Y₄ = nDeriv(Y₃,X,X)

Finding the Zero(s) of the Derivative

Because the radius of the can must be greater than zero, the domain of the surface area function is all x > 0. Notice that if the radius is very large, then the height is very small and vice versa.

Try different windows, viewing the graphs of the surface area function and its derivative in larger windows to assess global behavior, thinking about what the surface area must be for large and small values of x. You will discover that the derivative has only one zero. Find the approximate value of the zero of the derivative.

• Display the graphs of the surface area function and its derivative in a [0, 7, 1] x [-200, 400, 50] window.
• Use the Zero feature to find the zero of the derivative.

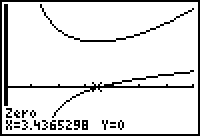
The critical point is x 3.4365.

Checking for Other Possible Extreme Values

From the graphs, the first derivative appears to be defined everywhere in the function's domain, so x 3.4365 is the only critical point. It can be shown that the surface area function is Y3 = 2 r² + 510/x and its derivative is Y4 = 4 x - 510/x². There are no endpoints to consider.

Using the Second Derivative

Test the critical point in the second derivative of the surface area function to justify that it represents a local minimum. Because the first derivative of surface area is stored in Y₄, the second derivative can be found by taking the derivative of Y₄.

• Enter nDeriv( Y₄, X, 3.4365) on the Home screen.

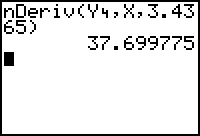
Because the second derivative of the surface area function is positive at x = 3.4365, the graph of the function is concave upward and has a local minimum value there. Because there are no endpoints and no other critical points, the local minimum value is the absolute minimum value.

Finding the Minimum Surface Area

Find the minimum surface area of the can by evaluating the surface area function, which is stored in Y₃, at the x-value that minimizes surface area.

• Enter Y₃(3.4365) on the Home screen.

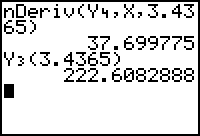
The minimum surface area of a cylindrical can that holds 255 cubic centimeters is approximately 222.61 square centimeters. The radius that will result in the minimum surface area is approximately 3.4365 centimeters and the corresponding height is Y₂(3.4365) 6.873 centimenters.

Finding the Ratio of Height to Radius

Evaluate the ratio of height to radius, , at the zero of the derivative of the surface area function.

• Enter the command Y₂(3.4365) / Y₁(3.4365) on the Home screen.

The ratio of height to radius for the can with minimum surface area is approximately 2.

14.2.1 Suppose the volume of the can is changed to 355 cubic centimeters. Find the radius that gives a minimum surface area of the new can and find the ratio of height to radius at the zero of the derivative for this new can.

Click here for the answer.

The Generalized Can Problem

It can be proven that the surface area of a can is minimized when the ratio of height to radius is 2, regardless of the volume. That is, for cylindrical cans with a fixed volume, when the height of the can is twice the radius, the surface area of the can will be minimized.