In this lesson you will explore finding the maximum possible volume of a cone that is made by removing a sector from a circular piece of paper. You will write a function for volume in terms of the length of the arc that is removed and use the zeros of the function's derivative to identify values that will be used to find the maximum volume.
Problems that ask for maximum or minimum values are called optimization problems, and each solution usually requires a multi-step procedure. This procedure can often be summarized as follows:
- Read the problem carefully and note which quantities vary and which are constant.
- Draw a diagram. Label the components with appropriate variables and constants.
- Identify the quantity to be maximized or minimized and write a function for it.
- Find the domain of the function in the problem.
- Graph the function on the domain in 4.
- Identify critical points and any endpoints. The critical points and endpoints are the candidates for any maximum and minimum values of the function.
- Use the graph, the first derivative, and perhaps the second derivative to find the maximum and/or minimum values.
- Answer the original question. Does your answer make sense? Is it justified?
It is easy to get involved in the individual steps and lose sight of this lengthy overall process. A graphing calculator can help you focus on the overall process by assisting with the individual steps. A graphing calculator can also make it possible to do more difficult problems that could not be done without using technology.
The Cone Problem
Suppose that a circular piece of paper has a radius of one unit. Removing a sector from the circular piece of paper and fastening together the remaining seams creates a cone. The following discussion will find the length of the arc of the removed sector that results in the cone of maximum volume. The maximum volume will also be found.
Drawing the Diagrams
Diagrams that represent the problem are shown below. The left illustration depicts the circular piece of paper with a sector removed and the right diagram illustrates the completed cone.
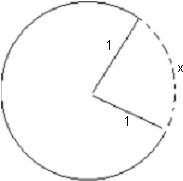
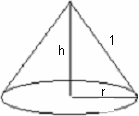
Volume of a Cone as a Function of Radius and Height
The quantity to be maximized is the volume of the cone. If the cone's height is h and r is its radius, its volume is given by
Suppose x represents the length of the arc removed. The variables r and h can each be written as functions of x and the volume can be written as a function of x, as well.
Radius as a Function of x
Note that the circumference of the original circular piece is 2
![]() and that the circumference of the base of the cone is equal to the arc of the circle remaining after the sector is removed. The circumference of the circular base of the cone can be written in two ways:
and that the circumference of the base of the cone is equal to the arc of the circle remaining after the sector is removed. The circumference of the circular base of the cone can be written in two ways:
-
The formula for finding the circumference of the circular base of a cone of radius r is c = 2
 r.
r.
-
The circumference of the circular piece of paper less the length of the removed arc is c = 2
 - x.
- x.
Because 2
![]() r and 2
r and 2
![]() - x represent the same quantity:
- x represent the same quantity:
Solving the equation for r gives
![]() , which expresses the radius r as a function of x.
, which expresses the radius r as a function of x.
Store the function for r in Y1.
-
Enter Y1 = 1 - X/(2
 ).
).
- Unselect Y1.
Height as a Function of x
Review the diagram of the cone shown below.
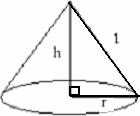
The equation h2 + r2 = 1, which is obtained from the Pythagorean theorem, can be used to define h as a function of r.
Because h can be written as a function of r and r is a function of x, h can be written as a function of x.
Because r(x) was entered into Y1 in the Y= editor, Y1 may be used to define the height function,
-
Enter
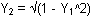
- Unselect Y2.
Volume as a Function of x
Volume was originally defined as a function of both r and h. Because r is a function of x and h is a function of r, volume can now be defined as a function of x.
The radius of the cone is stored in Y1 and the height of the cone is stored in Y2. Store the volume function,
![]() , into Y3 by using Y1 for r and Y2 for h.
, into Y3 by using Y1 for r and Y2 for h.
-
Enter Y3 = (
 /3) * Y12 * Y2
/3) * Y12 * Y2
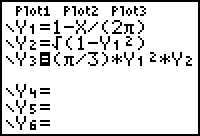
The Derivative of Volume with Respect to x
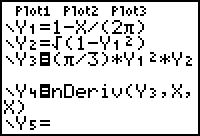
Store the derivative of the volume function, which is stored in Y3, into Y4 using the nDeriv feature of the Math menu.
- Enter Y4 = nDeriv(Y3,X,X).
The Domain of the Function in the Problem
Because the length of the arc that is removed must be greater than or equal to 0 and less than or equal to the circle's circumference, 2
![]() , the domain of the volume function is
, the domain of the volume function is
![]() .
.
Extreme Values of the Function on [0, 2
![]() ]
]
Any extreme value of the function must occur at a critical point or an endpoint. These values include:
- all zeros of the first derivative,
- all values where the first derivative is undefined, and
-
the endpoints 0 and 2
 of the function's domain.
of the function's domain.
Once all critical points are found, the function may be evaluated at those values and at the endpoints to determine where the maximum occurs.
Graphing the Function and Its Derivative
The maximum volume and its relationship to the corresponding zero of the first derivative can be illustrated by viewing the graphs of the volume function and its derivative.
-
Display the graphs defined in Y3 and Y4 in a [0, 2
 , 1] x [-0.2, 0.5, 0.1] window.
, 1] x [-0.2, 0.5, 0.1] window.
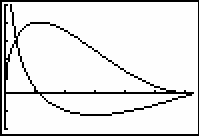
Based on the first derivative, there appears to be two points of interest:
- Although the derivative appears to be undefined at x = 0, that value is an endpoint and not a critical point.
- The derivative appears to have a zero near x = 1.
The Zero of the Derivative
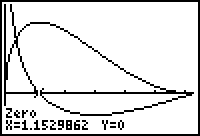
- Find the zero of the derivative by using the Zero feature in the CALC menu.
Maximum Volume
- Find the maximum value of the function by using the Maximum feature in the CALC menu.
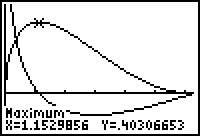
Although both are approximations, notice that the zero of the derivative is about the same as the x-value at the volume's maximum point.
The length of the removed arc that maximizes the volume is approximately 1.15299 units and the maximum volume is approximately 0.403067 cubic units, as shown at the bottom of the screen above.
Endpoint Values
Evaluate the volume function at the endpoints of the domain, 0 and 2
![]() , and observe that the cone has no volume for either of those values. The volume function is stored in Y3.
, and observe that the cone has no volume for either of those values. The volume function is stored in Y3.
-
Enter Y3(0) and Y3(2
 ) in the Home screen.
) in the Home screen.

The endpoints are minimums because the cone cannot have negative volume.
Conclusion
The endpoints do not yield a maximum. The function is zero at the two endpoints, and since it is positive at the only critical point, that point must be the absolute maximum. The maximum volume is about 0.403067 cubic units and it occurs when x
![]() 1.15299 units.
1.15299 units.
Using the Second Derivative
The second derivative can often be used to justify whether a critical point is a local maximum or a local minimum by revealing the function's concavity at that point. No conclusion can be drawn if the second derivative is zero or undefined at the critical point. The table below summarizes the relationships among the value of the second derivative at a critical point, the concavity of the function at the critical point, and whether a local minimum or local maximum occurs at the critical point.
| Second Derivative | Function | Max/Min |
| positive | concave upward | local minimum |
| negative | concave downward | local maximum |
14.1.1 Use the second derivative test to show that the volume has a local maximum at the critical point found above. Click here for the answer.
We found the maximum volume of a cone created by removing a sector and demonstrated the relationship between the first and second derivatives and the volume function. The approach used was graphical and numeric.
The analytic approach for this problem is rather complicated. It might be difficult to keep the overall process in mind while dealing with the lengthy functions for the first and second derivative. Technology handled the derivatives and that allowed us to focus on the procedure described at the beginning of the lesson as well as the relationship between the volume function and its derivatives.