In Lesson 7.1 you found vertical and horizontal asymptotes of a rational function. In this lesson you will see an

An oblique, or slanted, asymptote is a non-vertical and non-horizontal line that the graph of a function approaches as the magnitude of the input gets large without bound.

oblique asymptote, or slanted asymptote, of a rational function.

Investigating Oblique Asymptotes

You can make an oblique asymptote obvious by adjusting the Window values before graphing a function.

• Graph the rational function 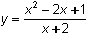in a [-10, 10, 1] x [-20, 10, 2] viewing window.

There appears to be a vertical asymptote at x = -2, which corresponds to the zero of the denominator in the rational function. However, there does not seem to be a horizontal asymptote.

Displaying an Oblique Asymptote

Although there is no horizontal asymptote, there is an important feature of this rational function as x gets large without bound in both the positive and negative directions that may not be obvious in the viewing window above.

• Change the Window values to [-100, 100, 10] x [-200, 100, 20].
• Display the graph of the function.

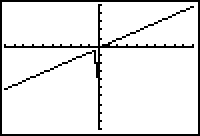
In this window the graph appears to be a line with a small wiggle near the y-axis. This slanted line is an oblique asymptote for the rational function .

Finding the Oblique Asymptote

You can find the equation of an oblique asymptote by converting the rational function to a polynomial plus a

A proper fraction is a rational expression in which the degree of the numerator is less than the degree of the denominator. An improper fraction is a rational expression in which the degree of the numerator is greater than or equal to the degree of the denominator. An improper fraction may be changed into a polynomial plus a proper fraction by dividing the numerator by the denominator. The quotient gives the polynomial, and the proper fraction is given by the remainder over the divisor.

proper fraction, which can be accomplished by polynomial long division.

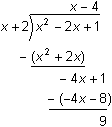
The quotient is x - 4 and the remainder is 9. This means the rational function is the sum of a linear polynomial function x - 4 and a proper fraction .

Since , the value of the original function is very close to the value of (x - 4) if |x| is large.

The linear function y = x - 4 is an equation of the oblique asymptote.

The Wide View

Graphical support that y = x - 4 is an oblique asymptote is provided by graphing both the line y = x - 4 and the rational function in a [-100, 100, 10] x [-200, 100, 20] window.

 

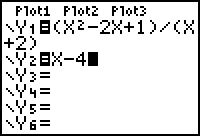
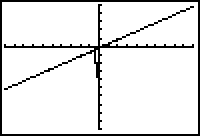
For values of x with large magnitude, the graphs of the rational function and the line appear to coincide in this window. (You can check this using the Trace feature.)

How the Graphs Differ

The difference between the graphs of the function and the line can be seen by displaying them in a smaller window.

• Display the graphs in a [-10, 10, 1] x [-20, 20, 2] window

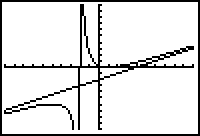
Notice that the appearance of the graph of a rational function is dramatically affected by the choice of window values. In a large viewing window the graph of the rational function looks like the graph of the line y = x - 4, but in a smaller window, the graphs are not similar.

The Narrow View

Now compare the graphs of the original rational function and the proper fraction near the vertical asymptote at x = -2.

• Change Y₂ in the Y= Editor to .
• Change the window values to [-3, -1, 1] x [-200, 100, 20].
• Display the graphs by pressing .

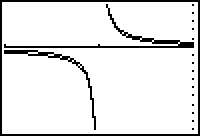
Near the vertical asymptote at x = -2 the graph of the rational function looks like the graph of the proper fraction .

7.3.1 Discribe the graph and asymptotes of then verify your answer by displaying the graph in a large window and in a smaller window near x = 2. Click here for the answer.