In this lesson you will investigate when a rational function has a hole in its graph and find a list of possible vertical asymptotes for a rational function.

In Lesson 7.1 you found the vertical asymptote of the rational function graphically, numerically, and analytically. The asymptote x = 3 corresponds to one of the zeros of the denominator, but the other zero of the denominator, x = -2, did not represent a vertical asymptote, as shown in the screen below.

Holes vs. Asymptotes

When x = -2, the function is undefined because the denominator is 0 but the limit of the function as x approaches -2 from the left and from the right is a single specific value. Since exists and is a single number, the line x = -2 is not a vertical asymptote.

7.2.1 Evaluate and discuss why x = -2 is not a vertical asymptote and determine the coordinates of the hole. Click here for the answer.

Displaying the Hole

In Lesson 7.1 you graphed the function in a [-20, 20, 5] x [-10, 10, 2] window.

• Display the graph again on your calculator by pressing .

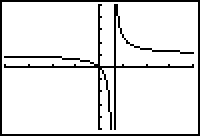
There is no apparent hole shown in this window, but if you change the viewing window, the hole may be seen.

• Display the graph in a Zoom Decimal window by pressing and selecting 4:ZDecimal.

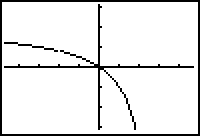
The hole at (-2, 0.80) should now be visible. If you trace to x = -2, you can see that the function is undefined there.

Zoom Decimal Zoom Decimal sets a [-4.7, 4.7, 1] x [-3.1, 3.1, 1] viewing window. In this window, the x-coordinates of points in this window will be tenths of a unit (..., -0.2; -0.1, 0, 0.1, 0.2,...) and the horizontal space between pixels will be 0.1.

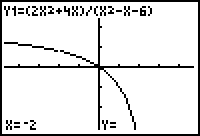
The choice of Window values will determine whether or not a hole in the graph of a function will actually be visible on the graphing screen.

7.2.2 Find the vertical asymptote and the hole in the graph of by factoring the numerator and denominator of the rational function and evaluating the limits. Support your findings by displaying the graph. Click here for the answer.