In this lesson you will investigate a

A rational function f is a function that can be written in the form , where p and q are polynomials and .

rational function that has both vertical and horizontal asymptotes. The asymptotes will be displayed graphically, then tables and analytic methods will be used to describe the behavior of the function near its asymptotes.

Conceptually, an asymptote is a line or a curve that the graph of a function approaches. Vertical asymptotes occur where function value magnitudes grow larger as x approaches a fixed number. Horizontal asymptotes occur when a function approaches a horizontal line as x approaches positive or negative infinity. Both types of asymptotes are discussed in this lesson and their formal definitions are given below.

Vertical Asymptote Definition

A function has a vertical asymptote at x = a if as the input values approach a from at least one side, the magnitude of the output increases without bound. That is, the line x = a is a vertical asymptote if

The diagram below illustrates the vertical asymptote of the function . Notice the function approaches negative infinity as x approaches 0 from the left and that it approaches positive infinity as x approaches 0 from the right.

Horizontal Asymptote Definition

A horizontal asymptote is a horizontal line that the graph of a function approaches as the magnitude of the input increases without bound in either a positive or negative direction. That is, the line y = k is a horizontal asymptote of f(x) if

A function may cross a horizontal asymptote for finite values of the input.

The function has a horizontal asymptote y = 0, as shown below.

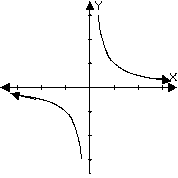
Comparing Vertical and Horizontal Asymptotes

A rational function is undefined at a vertical asymptote. The limits as or as will be the same if the function has a horizontal asymptote.

7.1.1 Graph the function in a [-20, 20, 5] x [-10, 10, 2] window. Use the graph to estimate the vertical and horizontal asymptotes and write their equations. Click here for the answer.

Calculators and Vertical Asymptotes When a function has a vertical asymptote, a graphing calculator will often show what appears to be the graph of the asymptote along with the graph of the function. However, the calculator is actually connecting the bottom branch of the graph with the top branch. These two branches should not be connected so the calculator graph is flawed. The graph of a vertical asymptote is not part of the graph of the function.

Vertical Asymptotes from a Table of Values

A table of values of the function near the vertical asymptote x = 3 can be useful in illustrating the function's behavior near the asymptote.

• Confirm that Y₁ = (2x² + 4x) / (x² - x - 6) is in the Y= editor.
• Display the Table Setup screen by pressing [TBLSET].
• Enter 2.98 for TblStart and 0.01 for Tbl.
• Select "Auto" for both Indpnt and Depend.
• Display the table by pressing [TABLE].

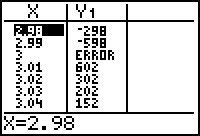
7.1.2 Describe the behavior of the function near the vertical asymptote x = 3. Click here for the answer.

Finding a Vertical Asymptote Analytically

Factoring the numerator and denominator of a rational function and simplifying the fraction can provide information about the function near a possible asymptote. For example, can be written as

Because is the same as except when x = -2, the expression can be used in left and right-hand limits to determine the behavior of the function near x = 3.

The Left-Hand Limit

As x approaches 3 from the left the numerator of approaches 6 while the denominator approaches 0 through negative values. This means the fraction will approach negative infinity.

The Right-Hand Limit

As x approaches 3 from the right the numerator of approaches 6 while the denominator approaches 0 through positive values. This means the fraction will approach positive infinity.

Therefore, x = 3 is a vertical asymptote of .

Horizontal Asymptotes from a Table of Values

Make a table of values to show the behavior of the function as it approaches the horizontal asymptote y = 2 when x is large and positive and when x is negative and large in absolute value.

• Set TblStart = 10 and Tbl = 20 and then display the table.
• Set TblStart = -10 and Tbl = -20 and then display the table.

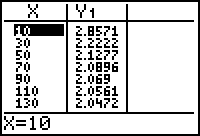
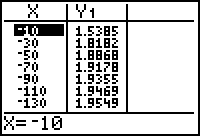
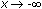
7.1.3 What do the two tables tell you about the behavior of the function as gets large? Click here for the answer.

Finding a Horizontal Asymptote Analytically

As the magnitude of x gets large, the term 2x² dominates the numerator and the term x² dominates the denominator. The end behavior of the rational function resembles the rational function . We say that y = 2 is an end behavior model for . In other words, the line
y = 2 is the horizontal asymptote of .