In this lesson you will begin with the graph of the absolute value function, , and then explore how to stretch and shrink the graph vertically, reflect the graph across the x-axis, and shift the graph vertically and horizontally. Stretches, shifts and reflections of a graph are called transformations.

The Absolute Value Function

Begin the exploration of transformations of graphs by displaying the graph of the absolute value function, .

• Open the STAT PLOT menu and turn off all active plots.
• Open the Y= editor, clear any old functions that may be in the editor and place the cursor by Y₁.

• Open the MATH NUM menu by pressing .

• Press to paste the absolute value command, abs, in Y₁.
• Complete the command Y₁=abs(x) by pressing .

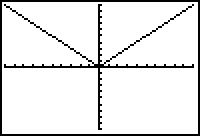
• Display the graph in a Zoom Standard window by pressing .

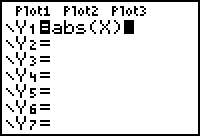
Stretch and Shrink Vertically

Explore the effect of multiplying the absolute value function by 2 and compare it with the basic absolute value graph. Make the graph of Y₁ = abs(X) thicker to distinguish it from the transformed graph.

Open the Y= editor and change the line style of Y₁ = abs(X) to thick.

• Place the cursor in the Y₁ function.
• Press the left arrow until the cursor is past the = sign.
• Press to select the thick style.
  Pressing repeatedly will rotate through the seven available styles.
• Return to the editor line by pressing when you have selected the style.
• Enter Y₂ = 2abs(X)
  Recall that abs( is the first item in the MATH NUM menu.

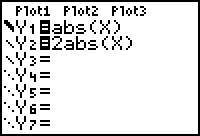
View the table of values for the two functions.

• Open the TABLE SETUP menu by pressing [TBLSET], which is above .
• Set TblStart to -3 and Tbl to 1.
• Indpnt and Depend should both be set to AUTO.
• Display the table of values for X, Y₁ and Y₂ by pressing [TABLE].
  

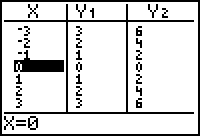
Notice that each Y2 value is 2 times the corresponding Y1 value.

• Display the graphs by pressing .
  
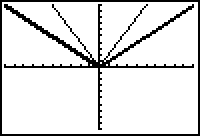
  Vertical Stretch by a factor of 2

The Stretch Factor

The table below shows points on the graph of Y₁ and the corresponding points on Y₂. The illustration shows the relative position of corresponding points.

The graph of is a vertical stretch of the graph of and the stretch factor is 2. Notice that the x-intercept is not stretched because 2(0) = 0.

3.1.1 Graph and in a Zoom Standard window and describe the resulting transformations. Click here for the answer.

Reflections

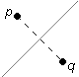
Another interesting transformation is a reflection, which is a mirror image.

The reflection of a point across a line sends the point p onto the point q, where the reflecting line is the perpendicular bisector of the line segment between p and q.

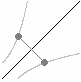
Reflecting a graph across a line reflects each point of the graph across the line.

Reflecting Across the x-Axis

Explore the effect of multiplying a function by -1.

• Enter Y₂= -abs(X) in the Y= editor.
• Display the table of values for X, Y₁, and Y₂ by pressing [TABLE].

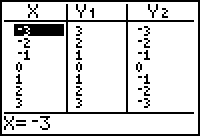
Each Y2 value is the negative of the corresponding Y1 value.

3.1.2 Graph and in a Zoom Standard window and describe the transformation. Click here for the answer.