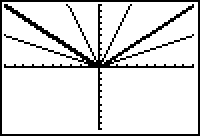
The graph of
![]() is a vertical stretch of
is a vertical stretch of
![]() by a factor of 3. The graph of
by a factor of 3. The graph of
![]() is a vertical shrink (or compression) of the graph of
is a vertical shrink (or compression) of the graph of
![]() by a factor of 1/2.
by a factor of 1/2.

![]() is a reflection across the x-axis of
is a reflection across the x-axis of
![]() .
.

![]() is a vertical shift of
is a vertical shift of
![]() up 5.
up 5.
![]() is a vertical shift of
is a vertical shift of
![]() down 4.
down 4.
- Reflected about the x-axis.
- Vertically compressed by a factor of 1/3.
- Shifted left 5.
- Shifted down 1.
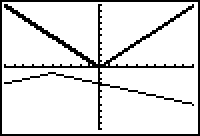
If
![]() the transformed graph will be a vertical shrink.
the transformed graph will be a vertical shrink.
If
![]() the transformed graph will be a vertical stretch.
the transformed graph will be a vertical stretch.
If a < 0, the transformed graph will be a reflection across the x-axis.
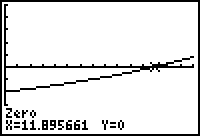
The investment will double in approximately 12 years, which agrees with the solution found from the table of values.
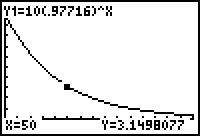
About 3.15 grams remain after 50 days.
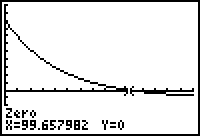
There will be 1 gram remaining after about 100 days.
- Make sure that the transformed regression equation is stored in Y2.
-
In the TBLSET editor, set TblStart = 0 and
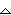 Tbl = 10.
Tbl = 10.
-
Display the table by pressing
 [TABLE].
[TABLE].
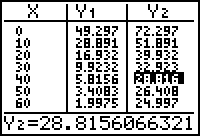
The x-value that yields an output close to 30 is x = 40. So the transformed regression equation predicts that the water will cool to approximately 30°C in a bit less than 40 minutes, which corresponds well with the data.
Any ordering of these 4 transformations will result in the correct graph as long as the vertical stretch and reflection are done before the vertical shift.
ReflectVertical stretch by factor of 2
Shift left 1
Shift down 3

©Copyright 2007 All rights reserved. | Trademarks | Privacy Policy | Link Policy