In this lesson you will enter data, create a scatter plot of the data, find the regression line that best fits the data, and display the regression line along with the scatter plot.

The Car-Value Example

To illustrate the procedure for creating a scatter plot of a data set and the regression equation that best models the data, the relationship between a car's age and its value will be explored. The following example will guide you to

1. illustrate data for a car's value versus its age by creating a scatter plot, and
2. find and display a linear equation that best fits the data by using linear regression.

Clearing the Lists

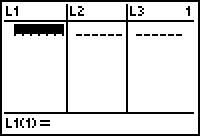
Before a scatter plot can be displayed or a regression equation can be created, the data must be entered into lists in the STAT List editor.

• Open the STAT EDIT menu by pressing .
• Open the List editor by selecting 1:Edit.

We want the List Editor to contain the lists L1-L6. If they aren't there, you need to reset the list names in the editor using the following Tech Tip.

Resetting List Names If the List editor contains lists other than L1 - L6, you can reset the editor with these list names by returning to the Home screen, pressing and selecting 5:SetUpEditor. That action pastes the command SetUpEditor to the Home screen. Press to execute the command. When you return to the List editor you should see lists named L1 through L6.

If the list L1 is not empty,

• Move the cursor to the top of the column until the heading "L1" is highlighted (by using the up arrow key) then press .

If other lists are not empty,

• Move the cursor to those lists with or and clear the lists as before.

Creating the Data Lists

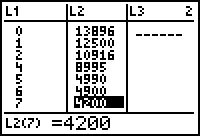
The following values (selling prices) for different ages of a particular model of car were taken from the classified ads of a newspaper. Enter the data into the lists L1 and L2 by following the directions below. The ages will be entered in the list L1 and the corresponding prices will be entered in the list L2.

• Position the cursor in the top row of L1 (but below the heading "L1") and enter the data for "Age". Press after each value to move to the next row.

Move the cursor to L2 with the right arrow key and enter the values for "Price".
Do not use a comma for the large values.

Editing Data in Lists If you make a mistake in a list, you can move the cursor to the bad entry with the cursor movement keys. Entering a new value will overwrite the old value. If you need to delete an entry, move the cursor to that entry and press . If you need to insert a new value within the list, move to the spot where the value is to be inserted and press [INS]. This will insert a "0" which can then be overwritten with the correct value.

Displaying a Scatter Plot of the Data

You can illustrate the data with a scatter plot displayed on the Graph screen. The process entails

1. defining the plot in the STAT PLOT editor,
2. setting the Viewing Window values, and
3. displaying the scatter plot.

Defining the Plot

• Press [STAT PLOT] to open the STAT PLOTS menu.
  [STAT PLOT] is above the key.


Define the scatter plot in Plot1. Details of the procedure are outlined below.

• Open the STAT PLOT editor for Plot1 by pressing .
• Move the cursor to "On" and select it by pressing .
• Move the cursor to the line labeled "Type".
  The first icon should be blinking. This icon represents a scatter plot.
• Select the scatter plot type and press .
• Move the cursor to the line labeled "Xlist" and press [L1] to enter L1 as the independent (or input) variable list.
  [L1] is above . This will result in having the values from L1, or the ages, plotted along the x-axis.
• Move the cursor to the line labeled "Ylist" and press [L2] to enter L2 as the dependent (or output) variable list.
  [L2] is above . This will result in having the values from L2, or the price, plotted along the y-axis.
• Move the cursor to the line labeled "Mark" and press to select the first icon.
  This is the mark that will be used for each point in the scatter plot.


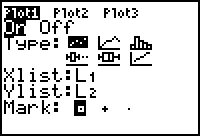
Plot1 should now be defined as shown above.

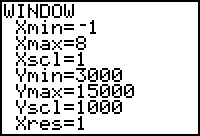
Set Up the Viewing Window

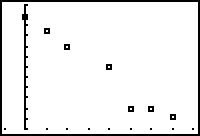
By looking at the data, an appropriate Viewing window for the scatter plot is [-1, 8, 1] x [3000, 15000, 1000].

• Press and enter the values.

Display the Scatter Plot

• Display the scatter plot by pressing .

Entering Window Values vs. Built-in Window Features The first few times students create a scatter plot they should directly enter the window values. After they understand how to select and enter appropriate window values for a scatter plot, they can use 9:ZoomStat in the Zoom menu. ZoomStat will automatically select and enter appropriate window values for the data set in the designated Xlist and Ylist and then display the scatter plot.

The Linear Regression Equation

The TI-83 has a feature that can be used to find the line that best fits the data. Such a line is called the "regression line" or "line of best fit." The following procedure

1. creates the regression line for the data in lists L1 and L2,
2. stores the equation in the Y= editor and
3. displays the graph of the line with the scatter plot on the Graph screen.

• Return to and clear the Home screen by pressing [QUIT] .
• Open the STAT CALC menu by pressing .

• Select 4:LinReg(ax+b) by pressing .
  This will paste the command LinReg(ax+b) to the Home screen.

You need to identify which list contains the x-values, which list contains the y-values, and where you would like to store the regression equation.

LinReg(ax+b) Syntax The syntax for creating the linear regression equation is LinReg(ax+b) Xlistname, Ylistname, [regEqu] where regEqu (regression equation) indicates the place where the regression equation will be stored. RegEqu is an optional parameter. Whether or not you specify a Y= function for regEqu, the regression equation is always stored to the TI-83 variable RegEQ, which is item 1 in the VARS Statistics EQ menu. Each time a regression equation is created, the calculator overwrites the prior regression equation in RegEQ with the new equation.

• Specify the X-list values by pressing [L1], which is above .
• Insert a comma between the list names by pressing .
• Specify the Y-list values by pressing [L2], which is above .
• Insert a comma after the Y-list name by pressing .
• Select Y₁ to hold the linear regression equation using the menus.

• Press to execute this command.
  

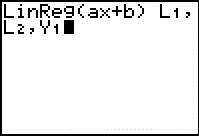
The equation is generated, displayed on the Home screen, and stored in Y1 in the Y= editor.


Home Screen

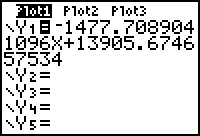
The Regression Equation in the Y= Editor

The linear equation that best fits the data is approximately

where x is the age of the car and y is its value.

• Press to display the graph of the regression equation with the scatter plot.

Turning Scatter Plots Off Sometimes students forget to turn off a scatter plot before graphing an equation for a new problem. This may interfere with a new graph. For example, if the lists are changed and STAT PLOT is left on you may get an error message such as "dimension mismatch" or "invalid dimension." To turn a scatter plot off: Return to the STAT PLOTS menu by pressing [STAT PLOT]. Open the desired Plot editor by pressing the number of the plot to be turned off. Move the cursor to "Off." Press . Exit the STAT PLOTS menu and return to the Home screen by pressing [QUIT]. Alternatively, press and use the up arrow key to get to the STAT PLOT. Then press to turn off the plot.

Med-Med

The Med-Med (median-median) feature in the STAT CALC menu fits the model equation y = ax + b to the data using the median-median line technique instead of the least-squares line of best fit technique used by linear regression. Med-Med displays values for a (slope) and b (y-intercept). The syntax for the Med-Med command is the same as the syntax for the LinReg(ax+b) command.

2.2.1 Perform Med-Med on the car-value data in this lesson and compare the resultant equation with the equation found using LinReg(ax+b), y = -1478x + 13,906. Click here for the answer.