Page 43 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : combinatoire et dénombrement
TI-83 Premium CE Edition Python TI-82 Advanced Edition Python
Niveau : spécialité maths Terminale
Le triangle de Pascal
L. DIDIER & R. CABANE
Fiche méthode
Proposition de résolution
Préalable informatique :
L’opérateur de division / en Python renvoie toujours un nombre à virgule (ou « flottante »). Comme on s’attend bien à ce que les coefficients binomiaux soient des entiers, on emploiera ici la « divi- sion entière » //, qui renvoie le quotient de la division euclidienne (a//b est la partie entière de a/b). De fait, nous ne l’emploierons que pour des divisions « tombant juste ».
Pour atteindre l’objectif 1 :
Dans cette partie nous allons présenter différentes manières pour calculer les coefficients binomiaux en essayant de les comparer. La fonction binome prend comme paramètres deux entiers naturels n et k et renvoie le coefficient binomial associé.
Pour atteindre l’objectif 2 :
Une fonction trianglepascal qui prend comme argument un entier naturel n et qui renvoie la liste des listes des coefficients binomiaux en affichant le triangle de Pascal.
Pour atteindre l’objectif 3 :
Une fonction conjecture prenant comme argument un entier naturel i
n et renvoyant la liste des ∑(i )pour tout i entier naturel (0≤i≤n). k=0 k
Objectif 1 : étapes de résolution
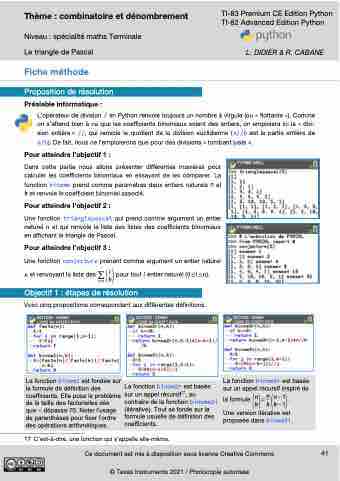
Voici cinq propositions correspondant aux différentes définitions.
La fonction binom1 est fondée sur la formule de définition des coefficients. Elle pose le problème de la taille des factorielles dès que n dépasse 70. Noter l’usage de parenthèses pour fixer l’ordre des opérations arithmétiques.
La fonction binom3r est basée sur un appel récursif inspiré de
n nn−1 laformule()= ( ).
Une version itérative est proposée dans binom3i.
La fonction binom2r est basée 17
surunappelrécursif ,au contraire de la fonction binome2i (itérative). Tout se fonde sur la formule usuelle de définition des coefficients.
k kk−1
17 C’est-à-dire, une fonction qui s’appelle elle-même.
Ce document est mis à disposition sous licence Creative Commons 41 © Texas Instruments 2021 / Photocopie autorisée