Page 39 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : logarithmes
TI-83 Premium CE Edition Python TI-82 Advanced Edition Python
Niveau : spécialité maths Terminale
Le calcul des logarithmes
L. DIDIER & R. CABANE
Fiche méthode
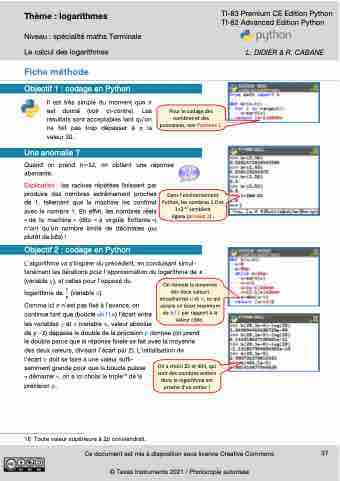
Objectif 1 : codage en Python
Il est très simple du moment que n
est donné (voir ci-contre). Les Pour le codage des
résultats sont acceptables tant qu’on ne fait pas trop dépasser à n la valeur 30.
Une anomalie ?
nombres et des puissances, voir l’annexe 1.
Quand on prend n=52, on obtient une réponse aberrante.
Explication : les racines répétées finissent par produire des nombres extrêmement proches de 1, tellement que la machine les confond avec le nombre 1. En effet, les nombres réels « de la machine » (dits « à virgule flottante ») n’ont qu’un nombre limité de décimales (ou plutôt de bits) !
Objectif 2 : codage en Python
Dans l’environnement Python, les nombres 1.0 et 1+2-52 semblent égaux (annexe 1) .
L’algorithme va s’inspirer du précédent, en conduisant simul- tanément les itérations pour l’approximation du logarithme de x
(variable y), et celles pour l’opposé du logarithme de 1x (variable z).
Comme ici n n’est pas fixé à l’avance, on
continue tant que (boucle while) l’écart entre
les variables y et z (variable e, valeur absolue
de y−z) dépasse le double de la précision p donnée (on prend le double parce que la réponse finale se fait avec la moyenne des deux valeurs, divisant l’écart par 2). L’initialisation de l’écart e doit se faire à une valeur suffi-
samment grande pour que la boucle puisse
« démarrer », on a ici choisi le triple16 de la
précision p.
On renvoie la moyenne des deux valeurs encadrantes u et v, ce qui assure un écart maximum de e/2 par rapport à la
valeur cible.
On a choisi 20 et 404, qui sont des nombres entiers donc le logarithme est proche d’un entier !
16 Toute valeur supérieure à 2p conviendrait.
Ce document est mis à disposition sous licence Creative Commons 37 © Texas Instruments 2021 / Photocopie autorisée