Page 36 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : intégrales
TI-83 Premium CE Edition Python TI-82 Advanced Edition Python
Niveau : spécialité maths Terminale
L'approximation des intégrales
L. DIDIER & R. CABANE
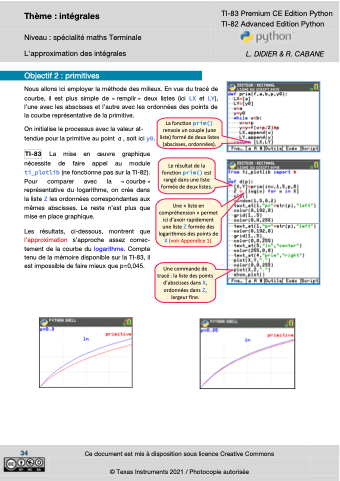
Objectif 2 : primitives
Nous allons ici employer la méthode des milieux. En vue du tracé de courbe, il est plus simple de « remplir » deux listes (ici LX et LY), l’une avec les abscisses et l’autre avec les ordonnées des points de la courbe représentative de la primitive.
On initialise le processus avec la valeur at- tendue pour la primitive au point a , soit ici y0.
TI-83 La mise en œuvre graphique nécessite de faire appel au module
ti_plotlib (ne fonctionne pas sur la TI-82). Pour comparer avec la « courbe » représentative du logarithme, on crée dans la liste Z les ordonnées correspondantes aux mêmes abscisses. Le reste n’est plus que mise en place graphique.
Les résultats, ci-dessous, montrent que l’approximation s’approche assez correc- tement de la courbe du logarithme. Compte tenu de la mémoire disponible sur la TI-83, il est impossible de faire mieux que p=0,045.
La fonction prim() renvoie un couple (une liste) formé de deux listes (abscisses, ordonnées).
Le résultat de la fonction prim() est rangé dans une liste formée de deux listes.
Une « liste en compréhension » permet ici d’avoir rapidement une liste Z formée des logarithmes des points de X (voir Appendice 1).
Une commande de tracé : la liste des points d’abscisses dans X, ordonnées dans Z, largeur fine.
34
Ce document est mis à disposition sous licence Creative Commons
© Texas Instruments 2021 / Photocopie autorisée