Page 30 - Activités algorithmiques avec Python en spécialité Mathématiques

Thème : suites et listes
TI-83 Premium CE Edition Python TI Nspire CX II-T
Niveau : Spécialité maths Terminale
Vitesses de croissance
L. DIDIER & R. CABANE
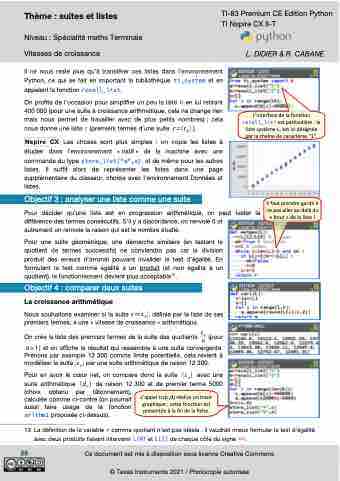
Il ne nous reste plus qu’à transférer ces listes dans l’environnement Python, ce qui se fait en important la bibliothèque ti_system et en appelant la fonction recall_list.
On profite de l’occasion pour simplifier un peu la liste b en lui retirant 400 000 (pour une suite à croissance arithmétique, cela ne change rien mais nous permet de travailler avec de plus petits nombres) ; cela nousdonneunelistec(premierstermesd’unesuite c=(cn)).
Nspire CX Les choses sont plus simples : on copie les listes à étudier dans l'environnement « natif » de la machine avec une
commande du type store_list("a",a). et de même pour les autres listes. Il suffit alors de représenter les listes dans une page supplémentaire du classeur, choisie avec l'environnement Données et listes.
Objectif 3 : analyser une liste comme une suite
Pour décider qu’une liste est en progression arithmétique, on peut tester la différence des termes consécutifs. S’il y a discordance, on renvoie 0 et
autrement on renvoie la raison qui est le nombre étudié.
Pour une suite géométrique, une démarche similaire (en testant le quotient de termes successifs) ne conviendra pas car la division produit des erreurs d’arrondi pouvant invalider le test d’égalité. En formulant le test comme égalité à un produit (et non égalité à un
13 quotient),lefonctionnementdevientplusacceptable .
Objectif 4 : comparer deux suites
La croissance arithmétique
Nous souhaitons examiner si la suite c=(cn), définie par la liste de ses premiers termes, a une « vitesse de croissance » arithmétique.
On crée la liste des premiers termes de la suite des quotients cn (pour n
n≥1 ) et on affiche le résultat qui ressemble à une suite convergente. Prenons par exemple 12 300 comme limite potentielle, cela revient à modéliser la suite (c n ) par une suite arithmétique de raison 12 300.
Pour en avoir le cœur net, on compare donc la suite (cn) avec une suite arithmétique (dn) de raison 12 300 et de premier terme 5000
L’interface de la fonction recall_list est particulière : la liste système L1 est ici désignée par la chaîne de caractères "1".
Il faut prendre garde à ne pas aller au-delà du « bout » de la liste !
(choix obtenu par tâtonnement), calculée comme ci-contre (on pourrait aussi faire usage de la fonction arithm1 proposée ci-dessus).
L’appel trc(c,d) réalise un tracé graphique ; cette fonction est présentée à la fin de la fiche.
13 La définition de la variable r comme quotient n’est pas idéale : il vaudrait mieux formuler le test d’égalité avec deux produits faisant intervenir L(0) et L[1] de chaque côté du signe ==.
28
Ce document est mis à disposition sous licence Creative Commons
© Texas Instruments 2021 / Photocopie autorisée