Um Daten zu analysieren, können Sie statistische Berechnungen durchführen. Das folgende Beispiel wendet ein lineares Regressionsmodell y=mx+b auf die beiden Listen in den Spalten A und B an.

1.

Wählen Sie im Menü Statistik die Option Statistische Berechnung > Lineare Regression (mx+b) aus, um das Regressionsmodell zu bestimmen.

Das Dialogfeld „Lineare Regression (mx+b)“ wird geöffnet.

2.

Geben Sie a[] als Spalte für die X-Liste ein.

3.

Geben Sie b[] als Spalte für die Y-Liste ein.

4.

Wenn Sie die Regressionsgleichung in einer bestimmten Variablen speichern möchten, ersetzen Sie RegEqn speichern unter durch den Namen der Variablen.

5.

Geben Sie c[] als Spalte für 1. Ergebnis ein.

6.

Klicken Sie auf OK.

Lists & Spreadsheet fügt zwei Spalten ein: eine mit den Namen der Ergebnisse und eine mit den entsprechenden Werten.

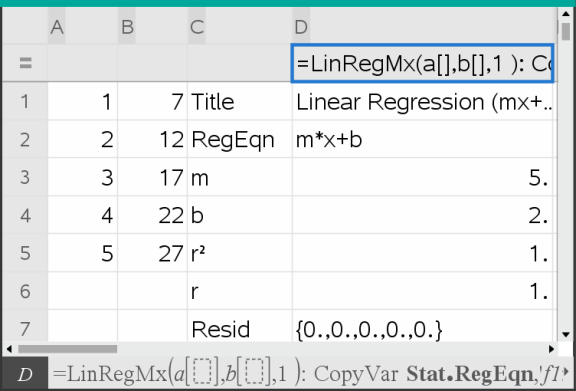
Hinweis: Die Ergebnisse sind mit den Quelldaten verknüpft. Sie können zum Beispiel einen Wert in Spalte A ändern; die Regressionsgleichung wird dann automatisch aktualisiert.

 

Lists & Spreadsheet speichert statistische Ergebnisse unter einem Variablen-Gruppennamen im Format stat.nnn, wobei nnn der Name des Ergebnisses ist (zum Beispiel stat.RegEqn und stat.Resid). Die Verwendung von Standardnamen für Variablen erleichtert die spätere Identifizierung und Verwendung der statistischen Variablen. Wenn Sie lieber eine benutzerdefinierte Variablengruppe verwenden möchten, können Sie die Formel in der Formelzelle der Spalte bearbeiten.

Sie können die folgende Formel verwenden, um die Ergebnisse in der Variablengruppe MystatsB zu speichern.

=LinRegMx(a[],b[],1): CopyVar Stat., MystatsB.

Später können Sie die Ergebnisse anzeigen, indem Sie den folgenden Ausdruck in die Calculator-Applikation oder in eine andere Spalte der Lists & Spreadsheet-Applikation eingeben:

MystatsB.results

 

Im Menü Statistische Berechnungen können Sie zwischen den nachstehend beschriebenen Berechnungsarten wählen. Weitere Informationen finden Sie im TI-Nspire™ -Handbuch .

OneVar, Statistik mit einer Variable

Analysiert Daten mit einer gemessenen Variable. Sie können auch eine optionale Häufigkeitsliste angeben. Die über diese Analysetechnik zurückgegebenen statistischen Daten sind:

•

Stichproben-Mittelwert, x

•

Summe der Daten, Gx

•

Summe der quadrierten Daten, Gx2

•

Stichproben-Standardabweichung, sx

•

Populations-Standardabweichung, sx

•

Stichprobengröße, n

•

X-min

•

Erstes Quartil, Q1

•

Median

•

Drittes Quartil, Q3

•

X-max

•

Summe der quadrierten Abweichungen, SSx = G(x Nx)2

TwoVar, Statistik mit zwei Variablen

Analysiert gepaarte Daten. Liste 1 ist die unabhängige Variable. Liste 2 ist die abhängige Variable. Sie können auch eine optionale Häufigkeitsliste angeben. Die über diese Analysetechnik zurückgegebenen statistischen Daten sind:

Für jede Liste:

•

Stichproben-Mittelwert, x oder y

•

Summe der Daten, Gx oder Gy

•

Summe der quadrierten Daten, Gx2 oder Gy2

•

Stichproben-Standardabweichung, sx = sn-1x oder sy = sn-1y

•

Populations-Standardabweichung, sx = snx oder sy = sny

•

X-min oder Y-min

•

erstes Quartil, Q1X oder Q1Y

•

Median

•

drittes Quartil, Q3X oder Q3Y

•

X-max oder Y-max

•

Summe der quadrierten Abweichungen, SSx = G(x Nx)2 oder SSy = G(y Ny)2

Zusätzliche Daten:

•

Stichprobengröße für jeden Datensatz, n

•

Gxy

•

Korrelationskoeffizient, R.

Lineare Regression (mx+b) (LinRegMx)

Passt die Modellgleichung y=ax+b mit der Methode der kleinsten Quadrate (least squares) an die Daten an. Sie zeigt Werte für m (Steigung) und b (y-Achsenabschnitt) an.

Lineare Regression (a+bx) (LinRegBx)

Passt die Modellgleichung y=a+bx mit der Methode der kleinsten Quadrate (least squares) an die Daten an. Sie zeigt die Werte für a (y-Achsenabschnitt), b (Steigung), r2 und r an.

Median-Median-Linie (MedMed)

Passt die Modellgleichung y=mx+b mittels der Median-Median-Linie (resistente Gerade) an die Daten an und berechnet dabei die Summenpunkte x1, y1, x2, y2, x3 und y3. Median-Median Linie zeigt Werte für m (Steigung) und b (y-Achsenabschnitt) an.

Quadratische Regression (QuadReg)

Passt das Polynom zweiten Grades y=ax2+bx+c an die Daten an. Sie zeigt Werte für a, b, c und R2 an. Für drei Datenpunkte ist die Gleichung eine Polynom-Anpassung, für vier und mehr eine Polynom-Regression. Es werden mindestens drei Datenpunkte benötigt.

Kubische Regression (CubicReg)

Passt das Polynom dritten Grades y=ax3+bx2+cx+d an die Daten an. Sie zeigt Werte für a, b, c, d und R2an. Für vier Datenpunkte ist die Gleichung eine Polynom-Anpassung, für fünf und mehr eine Polynom-Regression. Es werden mindestens vier Punkte benötigt.

Regression vierter Ordnung, QuartReg

Passt das Polynom vierten Grades y=ax4+bx3+cx2+dx+e an die Daten an. Sie zeigt Werte für a, b, c, d, e und R2 an. Für fünf Datenpunkte ist die Gleichung eine Polynom-Anpassung, für sechs und mehr eine Polynom-Regression. Es werden mindestens fünf Punkte benötigt.

Potenzregression, PowerReg

Passt die Modellgleichung y=axb mit der Methode der kleinsten Quadrate (least squares) der umgewandelten Werte ln(x) und ln(y) an die Daten an. Sie zeigt Werte für a, b, r2 und r an.

Exponentielle Regression (ExpReg)

Passt die Modellgleichung y=abx mit der Methode der kleinsten Quadrate (least squares) der umgewandelten Werte x und ln(y) an die Daten an. Sie zeigt Werte für a, b, r2 und r an.

Logarithmische Regression (LogReg)

Logarithmische Regression (LogReg) passt die Modellgleichung y=a+b ln(x) mittels mit der Methode der kleinsten Quadrate der umgewandelten Werte ln(x) und y an die Daten an. Sie zeigt Werte für a, b, r2 und r an.

Sinus-Regression (SinReg)

Passt die Modellgleichung y=a sin(bx+c)+d mit der iterativen Methode der kleinsten Quadrate (least squares) an die Daten an. Sie zeigt Werte für a, b, c und d an. Es werden mindestens vier Datenpunkte benötigt Es sind mindestens zwei Datenpunkte je Zyklus erforderlich, um Aliasingfrequenz-Schätzungen zu vermeiden.

Hinweis: Die Ausgabe von SinReg erfolgt unabhängig von der Moduseinstellung Bogenmaß/Grad immer im Bogenmaß.

Logistische Regression (d=0) (Logistisch)

Passt die Modellgleichung y=c/(1+a*e-bx) mit der iterativen Methode der kleinsten Quadrate (least squares) an die Daten an. Sie zeigt Werte für a, b und c an.

Logistische Regression (dƒ0) (LogistischD)

Passt die Modellgleichung y=c(1+a*e(-bx))+d mit der iterativen Methode der kleinsten Quadrate (least squares) an die Daten an. Sie zeigt Werte für a, b, c und d an.

Lineare Mehrfachregression (MultReg)

Berechnet die lineare Mehrfachregression der Liste Y für die Listen X1, X2, …, X10