Unterstützte statistische Tests
Hypothesenprüfungen sind in der Applikation Lists & Spreadsheet verfügbar. Weitere Informationen zu diesen Funktionen finden Sie im TI-Nspire™-Handbuch.
Einige Assistenten für statistische Tests enthalten ein Kontrollkästchen Zeichnen. Das Kontrollkästchen ist standardmäßig nicht ausgewählt. Durch Aktivieren dieses Kontrollkästchens wird auf der Seite ein Data & Statistics-Arbeitsbereich erstellt, in dem die Ergebnisse dargestellt werden.
z test (zTest)
Führt einen Hypothesentest für einen einzelnen unbekannten Populationsmittelwert m durch, wenn die Standardabweichung sder Population bekannt ist. Er testet die Null-Hypothese H0: m=m0 gegen eine der nachstehenden Alternativen.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Dieser Test wird bei großen normalverteilten Populationen verwendet. Die Standardabweichung muss bekannt sein.
Mit diesem Test können Sie ermitteln, ob eine Differenz zwischen einem Stichproben-Mittelwert und einem Populations-Mittelwert statistisch signifikant ist, wenn Sie die wahre Abweichung für eine Population kennen.
t test (tTest)
Führt einen Hypothesen-Test für einen einzelnen, unbekannten Populationsmittelwert m durch, wenn die Standardabweichung sunbekannt ist. Er testet die Null-Hypothese H0: m=m0 gegen eine der nachstehenden Alternativen.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Dieser Test ist dem z-Test ähnlich, wird jedoch verwendet, wenn die Population klein und normalverteilt ist. Dieser Test wird häufiger eingesetzt als der z-Test, da kleine Stichprobenpopulationen in Statistiken häufiger auftreten als große Populationen.
Dieser Test kann verwendet werden, um zu ermitteln, ob zwei normalverteilte Populationen gleiche Mittelwerte haben oder ob ein Stichproben-Mittelwert signifikant von einem Populations-Mittelwert abweicht und die Standardabweichung unbekannt ist.
2-Stichproben-Z-Test (zTest_2Samp)
Testet die Gleichwertigkeit der Mittelwerte zweier Populationen (m1 und m2) auf der Basis unabhängiger Stichproben, wenn beide Standardabweichungen (s1 und s2) bekannt sind. Die Null-Hypothese H0: m1=m2 wird gegen eine der nachstehenden Alternativen getestet.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
2-Stichproben-T-Test (tTest_2Samp)
Testet die Gleichwertigkeit der Mittelwerte zweier Populationen (m1 und m2) auf der Basis unabhängiger Stichproben, wenn keine der Standardabweichungen (s1 oder s2) bekannt sind. Die Null-Hypothese H0: m1=m2 wird gegen eine der nachstehenden Alternativen getestet.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
1-Prop z-Test (zTest_1Prop)
Berechnet einen Test für eine unbekannte Erfolgsrate (prop). Als Eingabe werden der Erfolgszähler in Stichprobe x und der Beobachtungszähler in Stichprobe n verwendet. 1-Prop-z-Test testet die Null-Hypothese H0: prop=p0 gegen eine der nachstehenden Alternativen.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Mit diesem Test kann ermittelt werden, ob die bei einer Stichprobe erkannte Erfolgswahrscheinlichkeit signifikant von der Erfolgswahrscheinlichkeit der Population abweicht oder ob dies an einem Stichprobenfehler, einer Abweichung oder an anderen Faktoren liegt.
2-Prop z-Test (zTest_2Prop)
Berechnet einen Test, um die Erfolgsraten (p1 und p2) zweier Populationen zu vergleichen. Als Eingabe wird der Erfolgszähler in jeder Stichprobe (x1 und x2) und der Beobachtungszähler in jeder Stichprobe (n1 und n2) verwendet. 2-Prop z-Test testet die Null-Hypothese H0: p1=p2 (mittels gepoolter Stichprobenanteile Ç) gegen eine der nachstehenden Alternativen.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Dieser Test hilft zu ermitteln, ob die in zwei Stichproben festgestellte Erfolgswahrscheinlichkeit gleich ist.
c2GOF (c2GOF)
Berechnet eine Testgröße, um zu überprüfen, ob die Stichprobendaten aus einer Grundgesamtheit stammen, die einer bestimmten Verteilung genügt. c2 GOF kann beispielsweise bestätigen, dass die Stichprobendaten aus einer Normalverteilung stammen.
c2 2-Wege-Test (c22-Wege)
Berechnet einen Chi-Quadrat-Test für Verbindungen in der Zweiwege-Zähler-Tabelle in der angegebenen Beobachtet-Matrix. Die Null-Hypothese H0 für eine Zweiwege-Tabelle lautet: Es besteht keine Verbindung zwischen Zeilenvariablen und Spaltenvariablen. Die Alternativ-Hypothese lautet: Die Variablen stehen zueinander in Verbindung.
2-Stichproben FTest (FTest_2Samp)
Berechnet einen F-Test zum Vergleich von zwei normalen Populations-Standardabweichungen (s1 und s2). Alle Populations-Mittelwerte und Standardabweichungen sind unbekannt. Der 2-StichprobenFTest verwendet das Verhältnis der Stichproben-Varianzen Sx12/Sx22 und testet die Null-Hypothese H0: s1=s2 gegen eine der nachstehenden Alternativen.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Nachstehend ist die Definition für den 2-Stichproben FTest aufgeführt.
|
Sx1, Sx2 |
= |
Stichproben-Standardabweichungen haben n1N1 bzw. n2N1 Freiheitsgrade (df). |
|
|
|
F-statistisch = |
|
df(x, n1N1, n2N1) |
= |
Fpdf ( ) mit den Freiheitsgraden df, n1N1 und n2N1 |
|
p |
= |
ausgegebener p-Wert |
2-Stichproben FTest für die Alternativ-Hypothese s1 > s2.
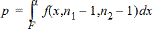
2-Stichproben FTest für die Alternativ-Hypothese s1 < s2.
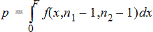
2-Stichproben FTest für die Alternativ-Hypothese s1ƒs2. Die Grenzen müssen folgende Bedingungen erfüllen:
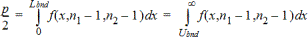
wobei: [Lbnd,Ubnd]=untere und obere Grenze
Die F--Statistik wird als die Grenze verwendet, die das kleinste Integral produziert. Die verbleibende Grenze wird gewählt, um die Gleichheitsbeziehung des vorangegangenen Integrals zu erreichen.
t-Test bei linearer Regression (LinRegtTest)
Berechnet eine lineare Regression für die gegebenen Daten und einen t-Test für den Steigungswert b sowie den Korrelationskoeffizienten r für die Gleichung y=a+bx. Er testet die Null-Hypothese H0: b=0 (gleichwertig, r=0) gegen eine der nachstehenden Alternativen.
| • | Ha: bƒ0 and rƒ0 |
| • | Ha: b<0 and r<0 |
| • | Ha: b>0 and r>0 |
Mehrfachregressionstests (MultRegTest)
Berechnet eine lineare Regression für die gegebenen Daten sowie die F-Test-Statistik für Linearität.
Weitere Informationen finden Sie im TI-Nspire™-Handbuch.
ANOVA (ANOVA)
Berechnet eine einfache Varianzanalyse, um die Mittelwerte von 2 bis 20 Populationen zu vergleichen. Das ANOVA-Verfahren zum Vergleichen dieser Mittelwerte schließt die Analyse der Streuung in den Stichprobendaten ein. Die Null-Hypothese H0: m1=m2=...=mk wird gegen die Alternative Ha: nicht alle m1...mk sind gleich.
Der ANOVA-Test ist ein Verfahren um zu entscheiden, ob die Varianz zwischen den Gruppen signifikant größer ist als die Varianz in den einzelnen Gruppen.
Mit diesem Test können Sie ermitteln, ob die Streuung von Daten zwischen verschiedenen Stichproben einen statistisch signifikanten Einfluss durch andere Faktoren hat, als die Streuung innerhalb der einzelnen Datensätze. Beispielsweise möchte ein Verpackungs-Einkäufer einer Versandfirma drei verschiedene Kartonhersteller beurteilen. Er erhält von allen drei Lieferanten Kartonproben. Mit ANOVA kann er ermitteln, ob die Unterschiede zwischen den einzelnen Stichproben im Vergleich zu den Unterschieden innerhalb jeder einzelnen Stichproben signifikant sind.
ANOVA 2-fach (ANOVA2way)
Berechnet eine zweifache Varianzanalyse, um die Mittelwerte von 2 bis 20 Populationen zu vergleichen. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert.
Die zweifache ANOVA-Varianzanalyse untersucht die Auswirkungen zweiter unabhängiger Variablen und hilft bei der Bestimmung, ob diese in Beziehung zur abhängigen Variable interagieren. (Mit anderen Worten: wenn die beiden unabhängigen Variablen interagieren, kann ihr kombinierter Effekt größer oder kleiner sein als der zusätzliche Einfluss jeder einzelnen unabhängigen Variablen.)
Mit diesem Test können Sie ähnliche Unterschiede wie mit der ANOVA-Analyse auswerten, jedoch mit einer weiteren möglichen Beeinflussung. Um das Karton-Beispiel aus der ANOVA-Analyse fortzusetzen, können Sie mit der Zweifach-ANOVA-Analyse den Einfluss des Kartonmaterials auf die erkannten Unterschiede untersuchen.
Auswählen einer Alternativ-Hypothese (ƒ < >)
Die meisten Inferenzstatistik-Editoren für die Hypothesentests fordern Sie zur Auswahl von einer von drei Alternativhypothesen auf.
| • | Die erste ist eine ƒ-Alternativhypothese, wie z.B. mƒm0 für den z Test. |
| • | Die zweite ist eine <Alternativhypothese, wie z.B. m1<m2 für den 2-Stichproben t Test. |
| • | Die dritte ist eine > Alternativhypothese, wie z.B. p1>p2 für den 2-Prop z Test. |
Um eine Alternativhypothese auszuwählen, bewegen Sie den Mauszeiger zur entsprechenden Alternative und drücken Sie die Eingabetaste.
Auswählen der Option Verteilt (Pooled)
Verteilt (nur bei 2-Stichproben t Test und 2-Stichproben t Intervall) legt fest, ob die Varianzen für die Berechnung zusammengefasst (gepoolt) werden sollen.
| • | Wählen Sie Nein, wenn Sie nicht möchten, dass die Varianzen gepoolt werden. Die Populationsvarianzen können ungleich sein. |
| • | Wählen Sie Ja, wenn Sie möchten, dass die Varianzen gepoolt werden. Es wird angenommen, dass die Populationsvarianzen gleich sind. |
Um die Option Verteilt (Pooled) auszuwählen, wählen Sie in der Dropdown-Liste „Ja“.