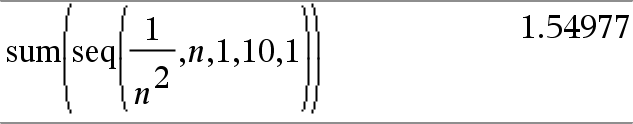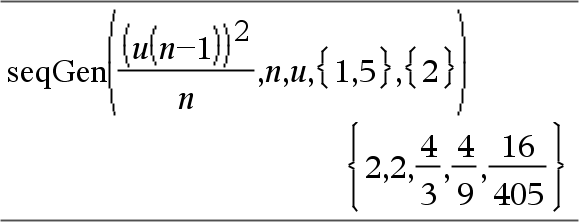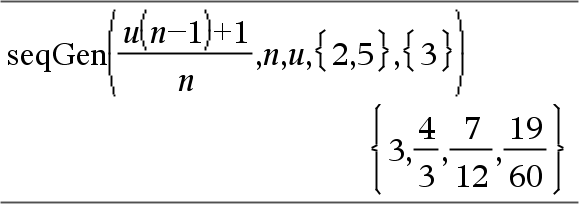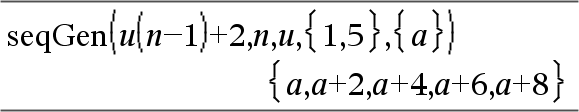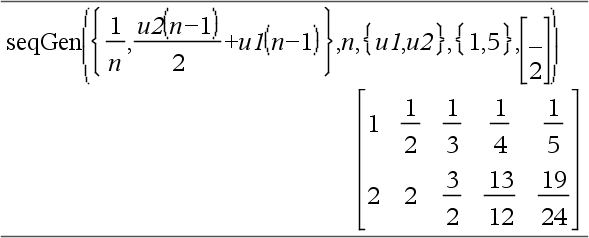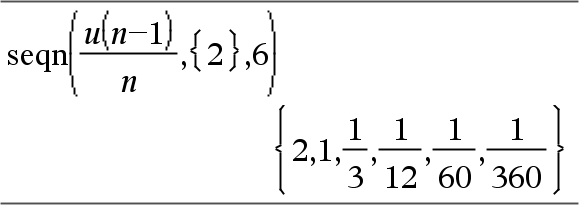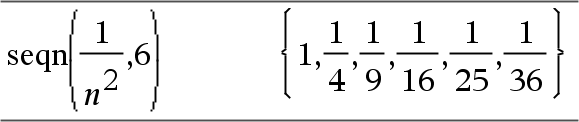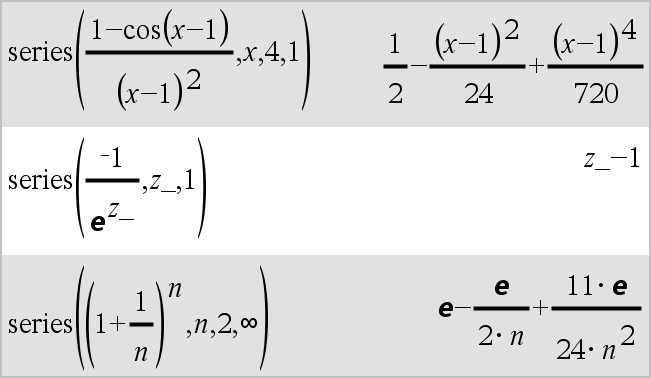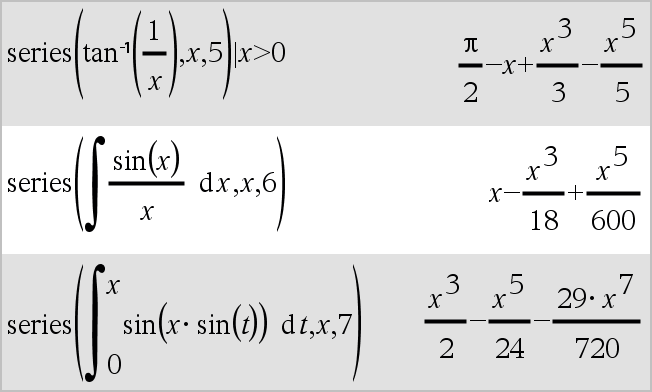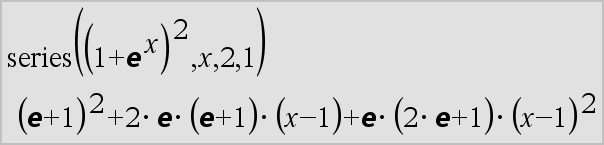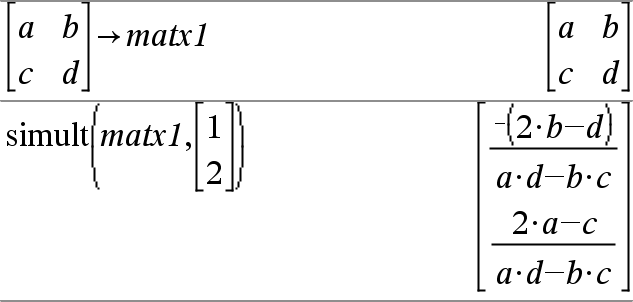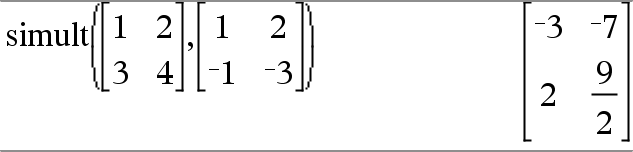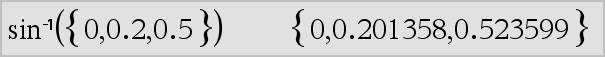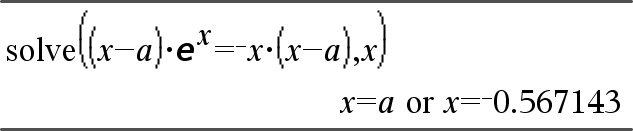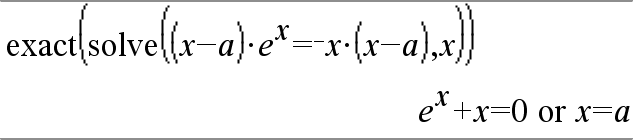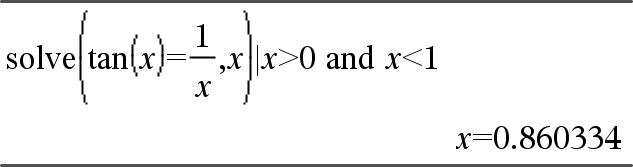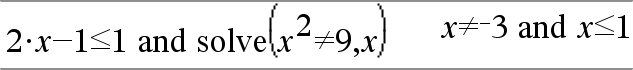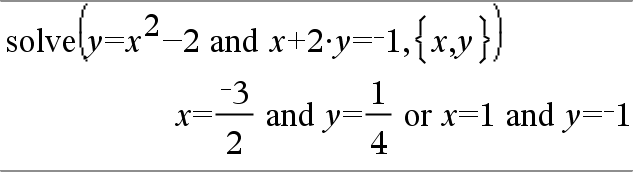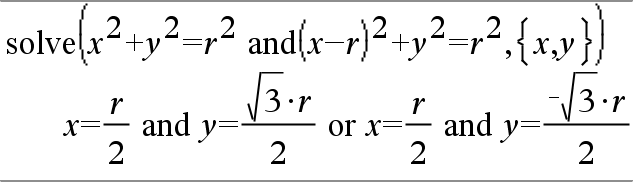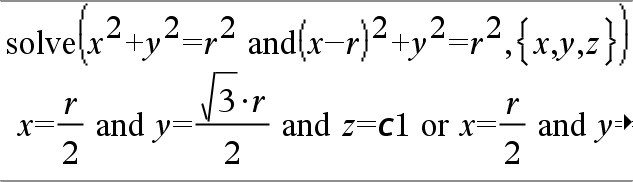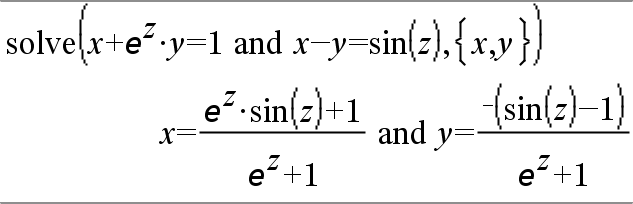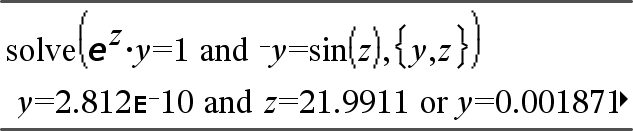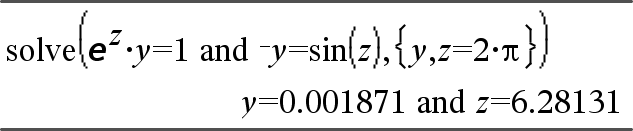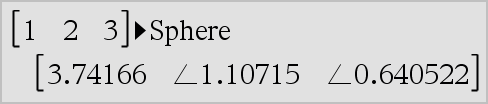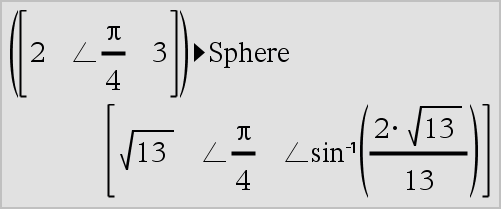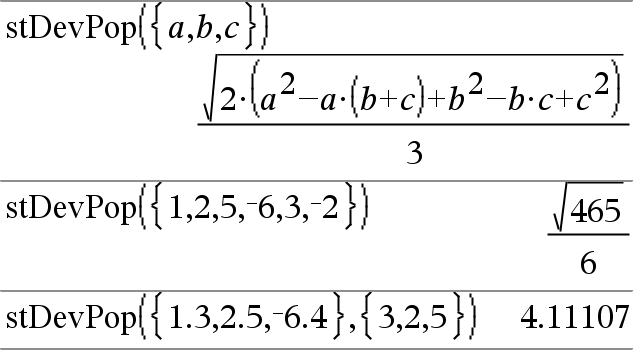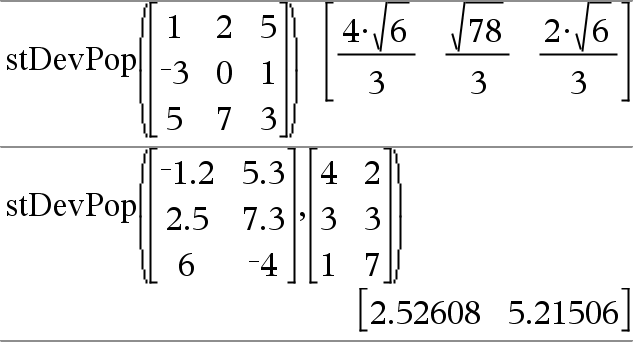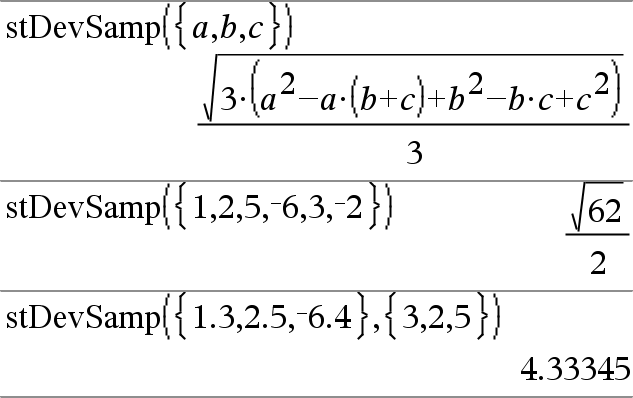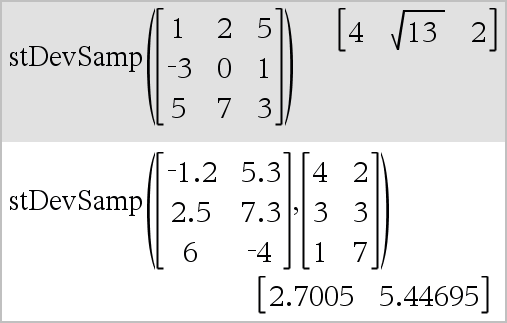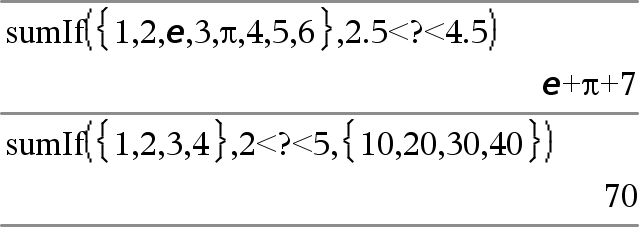|
µ tangent |
|
|
sec(Expr1) Þ uttryck sec(List1) Þ lista Ger sekansfunktionen för Expr1 eller en lista på sekansfunktionerna för alla element i List1. Obs: Argumentet tolkas som en vinkel i grader, nygrader eller radianer enligt det inställda vinkelläget. Du kan använda ¡, G eller R för att tillfälligt överstyra vinkelläget. |
I vinkelläget Grader:
|
|
µ tangent |
|
|
sec/(Expr1) Þ uttryck sec/(List1) Þ lista Ger den vinkel vars sekansfunktion är Expr1 eller en lista på de inversa sekansfunktionerna för alla element i List1. Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer beroende på det aktuella vinkelläget. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arcsec(...). |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
Katalog > |
|
|
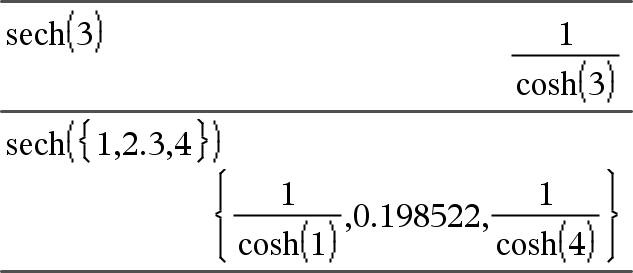
sech(Expr1) Þ uttryck sech(List1) Þ lista Ger den hyperboliska sekansfunktionen för Expr1 eller en lista på de hyperboliska sekansfunktionerna för elementen i List1. |
|
|
Katalog > |
|
|
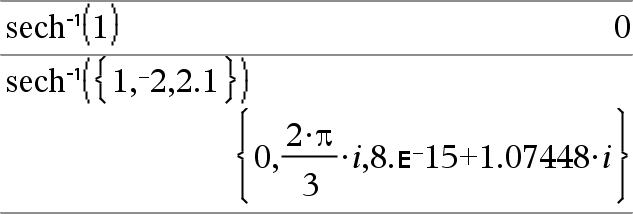
sech/(Expr1) Þ uttryck sech/ (List1) Þ lista Ger den inversa hyperboliska sekansfunktionen för Expr1 eller en lista på den inversa hyperboliska sekansfunktionen för alla element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arcsech(...). |
I vinkelläget Radianer och i Rektangulärt komplext läge:
|
|
Hubb-meny |
|
|
Programmeringskommando: Skickar ett eller flera TI-Innovator™ Hub kommandon till en ansluten hubb. exprOrString måste vara ett giltigt TI-Innovator™ Hub Kommando. exprOrString innehåller vanligen ett "SET ..." -kommando för att styra en enhet eller ett "READ ..." -kommando för att begära data. Argumenten skickas till hubben i turordning. Obs: Du kan använda kommandot Send i ett användardefinierat program, men inte i en funktion. |
Exempel: Slå på den blå komponenten i den inbyggda RGB-lysdioden i 0,5 sekunder.
Exempel: Begär nuvarande värde från hubbens inbyggda ljusnivåsensor. Ett Get-kommando hämtar värdet och tilldelar det till variabeln lightval.
Exempel: Skicka en beräknad frekvens till hubbens inbyggda högtalare. Använd den speciella variabeln iostr.SendAns för att visa hubb-kommandot med det beräknade uttrycket.
|
|
Katalog > |
|
|
seq(Expr, Var, Low, High[, Step])Þlista Ökar Var från Low till High i steg om Step, utvärderar Expr och ger resultaten som en lista. De ursprungliga innehållen i Var är fortfarande där när Det förinställda värdet på Step = 1. |
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
|
|
Katalog > |
|
|
Genererar en lista på termer för talföljden depVar(Var)=Expr enligt följande: Ökar den oberoende variabeln Var från Var0 till VarMax i steg om VarStep, utvärderar depVar(Var) för motsvarande värden på Var med formeln Expr och ListOfInitTerms och ger resultaten som en lista.
Genererar en matris med termer för ett system (eller en lista) av talföljder ListOfDepVars(Var)=ListOrSystemOfExpr enligt följande: Ökar den oberoende variabeln Var från Var0 till VarMax i steg om VarStep, utvärderar ListOfDepVars(Var) för motsvarande värden på Var med formeln ListOrSystemOfExpr och MatrixOfInitTerms och ger resultaten som en matris. De ursprungliga innehållen i Var är oförändrade när Det förinställda värdet på VarStep = 1. |
Genererar de första 5 termerna i talföljden u(n) = u(n-1)2/2, med u(1)=2 och VarStep=1.
Exempel i vilket Var0=2:
System med två talföljder:
Obs: Tomrummet (_) i den initiala termmatrisen ovan används för att indikera att den initiala termen för u1(n) beräknas med den explicita talföljdsformeln u1(n)=1/n. |
|
Katalog > |
|
|
Genererar en lista på termer för en talföljd, u(n)=Expr(u, n), enligt följande: Ökar n från 1 till nMax i steg om 1, utvärderar u(n) för motsvarande värden på n med formeln Expr(u, n) och ListOfInitTerms och ger resultaten som en lista.
Genererar en lista på termer för en icke-rekursiv talföljd, u(n)=Expr(n), enligt följande: Ökar n från 1 till nMax i steg om 1, utvärderar u(n) för motsvarande värden på n med formeln Expr(n) och ger resultaten som en lista. Om nMax saknas ställs nMax in på 2500 Om nMax=0 ställs nMax in på 2500 Obs: |
Genererar de första 6 termerna i talföljden u(n) = u(n-1)/2, med u(1)=2.
|
|
Catalog > |
|
|
series(Expr1, Var, Order [, Point])Þuttryck series(Expr1, Var, Order [, Point]) | Var>PointÞuttryck series(Expr1, Var, Order [, Point]) | Var<PointÞuttryck
Ger en generaliserad trunkerad potensserierepresentation av Expr1 utvecklat kring Point genom Order-graden Order kan vara ett rationellt tal vilket som helst. De resulterande potenserna av (Var N Point) kan inkludera negativa och/eller exponenter i bråkform. Koefficienterna för dessa potenser kan inkludera logaritmer av (Var N Point) och andra funktioner av Var som domineras av alla potenser av (Var N Point) som har samma exponenttecken. Point förinställs till 0. Point kan vara ˆ eller Nˆ, varvid utvecklingen sker genom Order-graden i 1/(Var N Point). series(...) ger “series(...)” om den inte kan bestämma en sådan representation, till exempel, för väsentliga singulariteter såsom sin(1/z) vid z=0, eN1/z vid z=0, eller ez vid z = ˆ eller Nˆ. Om serien eller någon av dess derivator har en språngdiskontinuitet vid Point innehåller resultatet troligen deluttryck i formen sign(…) eller abs(…) för en reell expansionsvariabel, eller (‑1)floor(…angle(…)…) för en komplex expansionsvariabel, vilken slutar med “_”. Om du tänker använda serien endast för värden på ena sidan av Point, lägg då till den lämpliga av “| Var > Point”, “| Var < Point”, “| “Var | Point” eller “Var { Point” för att erhålla ett enklare resultat. series() kan ge symboliska approximationer av obestämda och bestämda integraler, för vilka symboliska lösningar annars inte kan erhållas. series() fördelas över 1:a-argumentlistor och matriser. series() är en generaliserad version av taylor(). Som det sista exemplet till höger illustrerar kan visningsrutinerna nedåt i resultatet som produceras av series(...) arrangera om termer så att den dominanta termen inte är längst till vänster. |
|
|
Katalog > |
|
|
setMode(modeNameInteger, settingInteger) Þheltal setMode(list) Þlista på heltal Endast giltigt inom en funktion eller ett program. setMode(modeNameInteger, settingInteger) ställer temporärt in läget modeNameInteger på den nya inställningen settingInteger och ger ett heltal som motsvarar den ursprungliga inställningen på det läget. Ändringen är begränsad till den tid det tar att exekvera programmet/funktionen. modeNameInteger specificerar vilket läge du vill ställa in. Det måste vara något av de lägesheltal som anges i nedanstående tabell. settingInteger specificerar den nya inställningen för läget. Det måste vara något av de inställningsheltal som anges i nedanstående tabell för det läge som du ställer in. setMode(list) låter dig ändra flera inställningar. list innehåller par av lägesheltal och inställningsheltal.. setMode(list) ger en liknande lista vars heltalspar representerar de ursprungliga lägena och inställningarna. Om du har sparat alla lägesinställningar med getMode(0) & var kan du använda setMode(var) för att återställa dessa inställningar tills funktionen eller programmet avslutas. Se getMode(), här. Obs: De aktuella lägesinställningarna förs vidare till anropade delrutiner. Om någon delrutin ändrar en lägesinställning förloras lägesändringen när kontrollen återgår till den anropande delrutinen. Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
Visa ungefärligt värde på p med förinställningen för Display Digits (Visa siffror) och visa sedan p med inställningen Fix2. Kontrollera sedan att förinställningen har återställts efter exekveringen av programmet.
|
|
Lägets namn |
Läges- heltal |
Heltal för inställningar |
|
Display Digits (Visa siffror) |
1 |
1=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7, 9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12 |
|
Angle (Vinkel) |
2 |
1=Radian, 2=Degree, 3=Gradian |
|
Exponential Format (Exponentiellt format) |
3 |
1=Normal, 2=Scientific, 3=Engineering |
|
Real or Complex (Reellt eller Komplext) |
4 |
1=Real, 2=Rectangular, 3=Polar |
|
Auto or Approx. (Auto eller Ungefärlig) |
5 |
1=Auto, 2=Approximate |
|
Vector Format (Vektorformat) |
6 |
1=Rectangular, 2=Cylindrical, 3=Spherical |
|
Base (Bas) |
7 |
1=Decimal, 2=Hex, 3=Binary |
|
Unit System (Enhetssystem) |
8 |
1=SI, 2=Eng/US |
|
Katalog > |
|
|
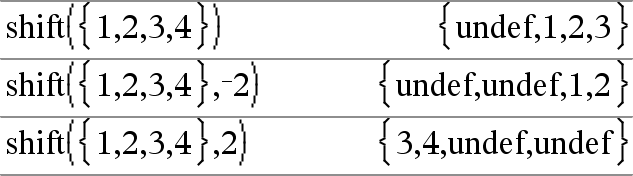
shift(Integer1[,#ofShifts])Þheltal Skiftar bitarna i ett binärt heltal. Du kan skriva in Integer1 i valfri talbas. Det omvandlas automatiskt till 64-bitars binär form. Om storleken på Integer1 är alltför stor för denna form för en symmetrisk modulooperation talet inom området. För mer information, se 4Base2, här. Om #ofShifts är positiv sker skiftningen åt vänster. Om #ofShifts är negativ sker skiftningen åt höger. Förinställningen är L1 (skifta en bit åt höger). Vid en skiftning åt höger “droppas” biten längst till höger och 1 infogas som denna bit. Vid skiftning åt vänster “droppas” biten längst till vänster och 0 infogas som denna bit. Vid exempelvis skiftning åt höger: Varje bit skiftas åt höger. 0b0000000000000111101011000011010 Infogar 0 om biten längst till vänster är 0 eller 1 om denna bit är 1. ger: 0b00000000000000111101011000011010 Resultatet visas enligt det inställda basläget. Inledande nollor visas inte. |
I binärt basläge:
I hexadecimalt basläge:
Viktigt: För att skriva in ett binärt eller hexadecimalt tal, använd alltid prefixet 0b eller 0h (noll, inte bokstaven O). |
|
shift(List1 [,#ofShifts])Þlista Ger en kopia av List1 skiftad åt höger eller vänster av #ofShifts-elementen. Ändrar inte List1. Om #ofShifts är positiv sker skiftningen åt vänster. Om #ofShifts är negativ sker skiftningen åt höger. Förinställningen är L1 (skifta ett element åt höger). Element som infogas i början eller slutet av list av skiftningen tilldelas symbolen “undef”. |
I decimalt basläge:
|
|
shift(String1 [,#ofShifts])Þsträng Ger en kopia av String1 skiftad åt höger eller vänster av #ofShifts-tecknen. Ändrar inte String1. Om #ofShifts är positiv sker skiftningen åt vänster. Om #ofShifts är negativ sker skiftningen åt höger. Förinställningen är L1 (skifta ett tecken åt höger). Tecken som infogas i början eller slutet av string av skiftningen får ett mellanslag. |
|
|
Katalog > |
|
|
sign(Expr1)Þuttryck sign(List1)Þlista sign(Matrix1)Þmatris Ger, för ett reellt eller komplext Expr1, Expr1/abs(Expr1) när Expr1ƒ 0. Ger 1 om Expr1 är positivt. Ger L1 om Expr1 är negativt. sign(0) ger „1 om det komplexa formatläget är Real, annars ger det sig självt. sign(0) representerar enhetscirkeln i det komplexa området. Ger, för en lista eller matris, tecknen för alla element. |
Om det komplexa formatläget är Real:
|
|
Katalog > |
|||||||
|
simult(coeffMatrix, constVector[, Tol])Þmatris Ger en kolumnvektor som innehåller lösningarna för ett system av linjära ekvationer. Obs: Se även coeffMatrix måste vara en kvadratmatis som innehåller koefficienterna för ekvationerna. constVector måste ha samma antal rader (samma dimension) som coeffMatrix och innehålla konstanterna. Alternativt behandlas varje matriselement som noll om dess absolutvärde är mindre än Tol. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras Tol.
|
Lös för x och y: x + 2y = 1 3x + 4y = L1
Lösningen är x=L3 och y=2.
Lös: ax + by = 1 cx + dy = 2
|
||||||
|
simult(coeffMatrix, constMatrix[, Tol])Þmatris Löser multipla system av linjära ekvationer där varje system har samma koefficienter för variablerna, men olika konstanter. Varje kolumn i constMatrix måste innehålla konstanterna för ett ekvationssystem. Varje kolumn i den resulterande matrisen innehåller lösningen på motsvarande system. |
Lös: x + 2y = 1 3x + 4y = L1
x + 2y = 2 3x + 4y = L3
För det första systemet är lösningen x=L3 och y=2. För det andra systemet är lösningen x=L7 och y=9/2. |
|
Katalog > |
|
|
Expr 4sin Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>sin. Representerar Expr i termer av sinus. Detta är en omvandlingsoperator för visning. Den kan endast användas i slutet av inmatningsraden. 4sin reducerar alla potenser av cos(...) modulo 1Nsin(...)^2 så att eventuella återstående potenser av sin(...) har exponenter i området (0, 2). Resultatet kommer sålunda att vara fritt från cos(...) om, och endast om, cos(...) endast inträffar i det givna uttrycket vid jämna potenser. Obs: Denna omvandlingsoperator stöds inte i vinkellägena Grader och Nygrader. Innan du använder den, kontrollera att vinkelläget är inställt på Radianer och att Expr inte innehåller explicita referenser till vinklar i grader eller nygrader. |
|
|
tangent µ |
|
|
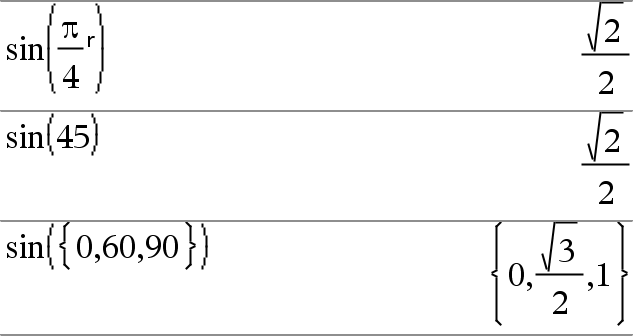
sin(Expr1)Þuttryck sin(List1)Þlista
sin(List1) ger en lista på sinus för alla element i List1. Obs: Argumentet tolkas som en vinkel i antingen grader, nygrader eller radianer beroende på det aktuella vinkelläget. Du kan använda ¡,G eller R för att tillfälligt överstyra vinkelläget. |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
sin(squareMatrix1)ÞkvadratMatris Ger matrisen med sinus för squareMatrix1. Detta är inte detsamma som att beräkna sinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer:
|
|
tangent µ |
|
|
sin/(Expr1)Þuttryck sin/(List1)Þlista
sin/(List1) ger en lista på invers sinus för varje element i List1. Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer beroende på det aktuella vinkelläget. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arcsin(...). |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
sin/(squareMatrix1)ÞkvadratMatris Ger matrisen med invers sinus för squareMatrix1. Detta är inte detsamma som att beräkna invers sinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer och i Rektangulärt komplext format:
|
|
Katalog > |
|
|
sinh(Expr1)Þuttryck sinh(List1)Þlista
sinh (List1) ger en lista på hyperboliska sinus för varje element i List1. |
|
|
sinh(squareMatrix1)ÞkvadratMatris Ger matrisen med hyperbolisk sinus för squareMatrix1. Detta är inte detsamma som att beräkna hyperbolisk sinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer:
|
|
Katalog > |
|
|
sinh/(Expr1)Þuttryck sinh/(List1)Þlista
sinh/(List1) ger en lista på invers hyperbolisk sinus för varje element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arcsinh(...). |
|
|
sinh/(squareMatrix1)ÞkvadratMatris Ger matrisen med invers hyperbolisk sinus för squareMatrix1. Detta är inte detsamma som att beräkna invers hyperbolisk sinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet innehåller alltid tal med flytande komma. |
I vinkelläget Radianer:
|
|
Katalog > |
|
|
SinReg X, Y [, [Iterations],[ Period] [, Category, Include] ] Utför en trigonometrisk regressionsanalys på listorna X och Y. En sammanfattning av resultaten visas i variabeln stat.results. (Se här.) Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Iterations är ett värde som specificerar det maximala antalet gånger (1 till och med 16) en lösning kommer att provas. Om denna utelämnas används 8. Normalt ger större värden bättre noggrannhet, men längre exekveringstider, och vice versa. Period specificerar en uppskattad period. Om denna utelämnas bör skillnaden mellan värdena i X vara lika och i ordningsföljd. Om du specificerar Period kan skillnaderna mellan x-värden vara olika. Category är en lista på kategorikoder för motsvarande X- och Y-data. Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen. Resultatet av SinReg är alltid i radianer oavsett det inställda vinkelläget. För information om effekten av tomma element i en lista, se “Tomma element” (här). |
|
|
Resultatvariabel |
Beskrivning |
|
stat.RegEqn |
Regressionsekvation: a·sin(bx+c)+d |
|
stat.a, stat.b, stat.c, stat.d |
Regressionskoefficienter |
|
stat.Resid |
Residualer från regressionen |
|
stat.XReg |
Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i Freq, Category List och Include Categories |
|
stat.YReg |
Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i Freq, Category List och Include Categories |
|
stat.FreqReg |
Lista på frekvenser som motsvarar stat.XReg och stat.YReg |
|
Katalog > |
|
|
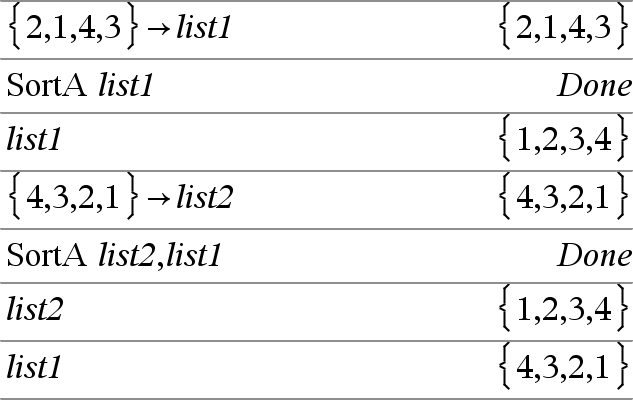
SortA List1[, List2] [, List3] ... SortA Vector1[, Vector2] [, Vector3] ... Sorterar elementen i det första argumentet i stigande ordning. Om du inkluderar ytterligare argument sorteras elementen i varje argument så att deras nya positioner matchar de nya positionerna för elementen i det första argumentet. Alla argument måste vara namn på listor eller vektorer. Alla argument måste ha samma dimensioner. Tomma element inom det första argumentet flyttas till botten. För mer information om tomma element, se här. |
|
|
Katalog > |
|
|
SortD List1[, List2] [, List3] ... SortD Vector1[,Vector2] [,Vector3] ... Identisk med SortA med undantag för att SortD sorterar elementen i fallande ordning. Tomma element inom det första argumentet flyttas till botten. För mer information om tomma element, se här. |
|
|
Katalog > |
|
|
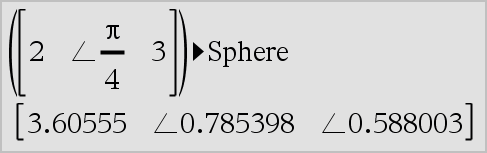
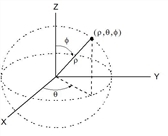
Vector 4Sphere Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Sphere. Visar rad- eller kolumnvektorn i sfärisk form [r ±q ±f]. Vector måste ha dimensionen 3 och kan vara antingen en rad- eller en kolumnvektor. Obs: 4Sphere är en visa format-instruktion, inte en konverteringsfunktion. Du kan endast använda den i slutet av en inmatningsrad. |
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
Tryck på ·
|
|
Katalog > |
|
|
sqrt(Expr1)Þuttryck sqrt(List1)Þlista Ger kvadratroten ur argumentet. Ger, för en lista, kvadratrötterna ur alla element i List1. Obs: Se även Square root template, här. |
|
|
Katalog > |
|
|
stat.results Visar resultaten av en statistisk beräkning. Resultaten visas som en uppsättning av namn-värdepar. De specifika namnen som visas beror på den/det senast utvärderade statistiska funktionen/kommandot. Du kan kopiera ett namn eller ett värde och klistra in det på andra platser.
Obs: Undvik att definiera variabler med samma namn som de variabler vilka används för statistisk analys. I vissa fall kan ett feltillstånd uppstå. Variabelnamn som används för statistisk analys listas i nedanstående tabell. |
|
|
stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d |
stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX |
stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y |
stat.Q3X stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS |
stat.SSBlock stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1 stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w stat.y stat.yList stat.YReg |
|
Obs: Varje gång applikationen Listor och kalkylblad beräknar statistiska resultat kopierar den “stat.”-gruppvariabler till en “stat#.”-grupp där # är ett tal som ökas automatiskt. Detta låter dig bibehålla tidigare resultat medan du utför flera beräkningar. |
|
Katalog > |
|
|
stat.values Visar en matris över värdena beräknade för den/det senast utvärderade statistiska funktionen/kommandot. Till skillnad från stat.results utelämnar stat.values namnen som är associerade med värdena. Du kan kopiera ett värde och klistra in det på andra platser. |
Se exemplet stat.results. |
|
Katalog > |
|
|
stDevPop(List[, freqList])Þuttryck Ger populationens standardavvikelse för elementen i List. Varje freqList-element räknar antalet förekomster av motsvarande element i List. Obs: List måste innehålla minst två element. Tomma element ignoreras. För mer information om tomma element, se här. |
I vinkelläget Radianer och i Auto-läge:
|
|
stDevPop(Matrix1[, freqMatrix])Þmatris Ger en radvektor med populationens standardavvikelser för kolumnerna i Matrix1. Varje freqMatrix-element räknar antalet förekomster av motsvarande element i Matrix1. Obs: Matrix1 måste innehålla minst två rader. Tomma element ignoreras. För mer information om tomma element, se här. |
|
|
Katalog > |
|
|
stDevSamp(List[, freqList])Þuttryck Ger urvalets standardavvikelse för elementen i List. Varje freqList-element räknar antalet förekomster av motsvarande element i List. Obs: List måste innehålla minst två element. Tomma element ignoreras. För mer information om tomma element, se här. |
|
|
stDevSamp(Matrix1[, freqMatrix])Þmatris Ger en radvektor med urvalets standardavvikelser för kolumnerna i Matrix1. Varje freqMatrix-element räknar antalet förekomster av motsvarande element i Matrix1. Obs: Matrix1 måste innehålla minst två rader. Tomma element ignoreras. För mer information om tomma element, se här. |
|
|
Katalog > |
|
|
Stop Programmeringskommando: Avslutar programmet. Stop är ej tillåtet i funktioner. Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
|
|
Se & (store), här. |
|
|
|
|
|
Katalog > |
|
|
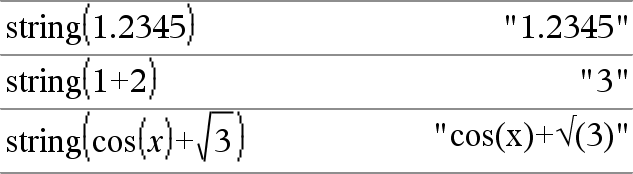
string(Expr)Þsträng Förenklar Expr och ger resultatet som en teckensträng. |
|
|
Katalog > |
|
|
subMat(Matrix1[, startRow] [, startCol] [, endRow] [, endCol]) Þmatris Ger specificerad undermatris av Matrix1. Förvalsinställningar: startRow=1, startCol=1, endRow=sista rad, endCol=sista kolumn. |
|
|
Se G(), här. |
|
|
|
|
|
Katalog > |
|
|
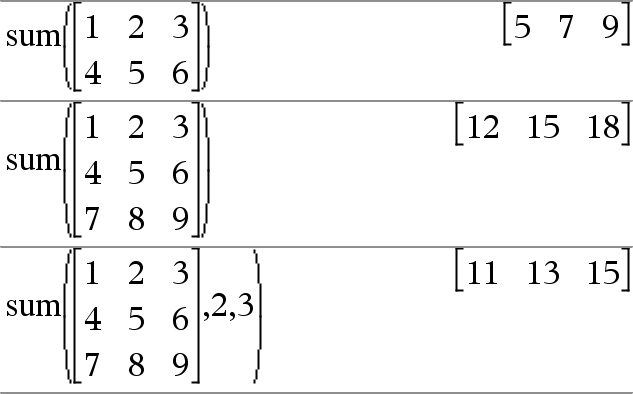
sum(List[, Start[, End]])Þuttryck Ger summan av elementen i List. Start och end är valfria. De specificerar ett område med element. Varje tomt argument ger ett tomt resultat. Tomma element i List ignoreras. För mer information om tomma element, se här. |
|
|
sum(Matrix1[, Start[, End]])Þmatris Ger en radvektor som innehåller summorna av elementen i kolumnerna i Matrix1. Start och end är valfria. De specificerar ett område med rader. Varje tomt argument ger ett tomt resultat. Tomma element i Matrix1 ignoreras. För mer information om tomma element, se här. |
|
|
Katalog > |
|||||||
|
sumIf(List,Criteria[, SumList])Þvärde Ger den totala kumulerade summan av alla element i List som uppfyller specificerade Criteria. Du kan också specificera en alternativ lista, sumList, för att ge elementen som skall kumuleras. List kan vara ett uttryck, en lista eller en matris. SumList, om specificerad, måste ha samma dimension(er) som List. Criteria kan vara:
När ett List-element uppfyller Criteria adderas elementet till den ackumulerade summan. Om du inkluderar sumList adderas i stället motsvarande element från sumList till summan. I applikationen Listor och kalkylblad kan du använda ett område av celler i stället för List och sumList. Tomma element ignoreras. För mer information om tomma element, se här. Obs: Se även countIf(), här. |
|
|
Se G(), här. |
|
|
|
|
|
Katalog > |
|
|
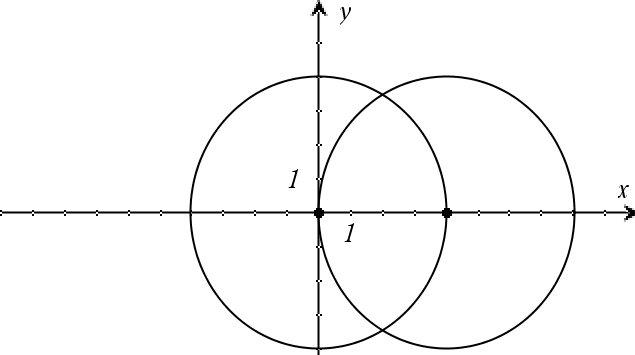
system(Eqn1 [, Eqn2 [, Eqn3 [, ...]]]) system(Expr1 [, Expr2 [, Expr3 [, ...]]]) Ger ett ekvationssystem formaterat som en lista. Du kan också skapa ett system med en mall.
|
|
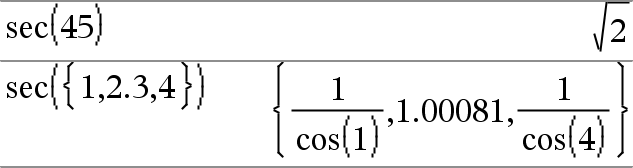







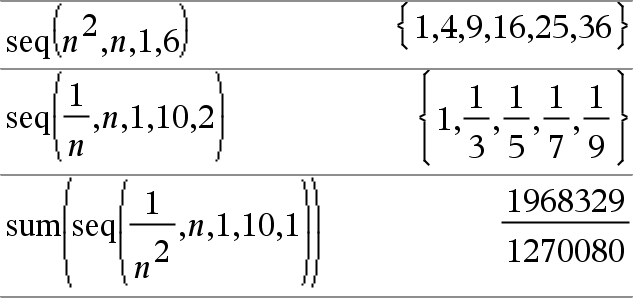
 .
.