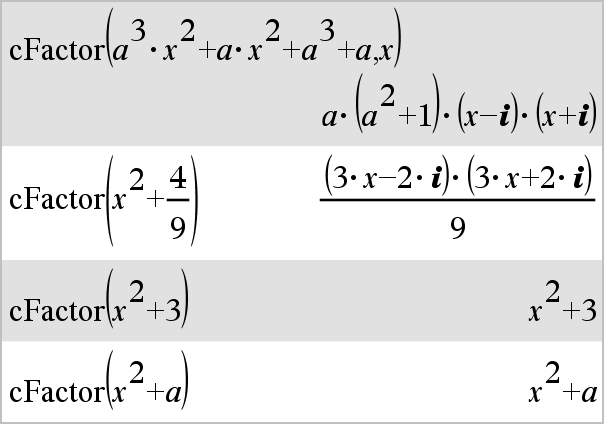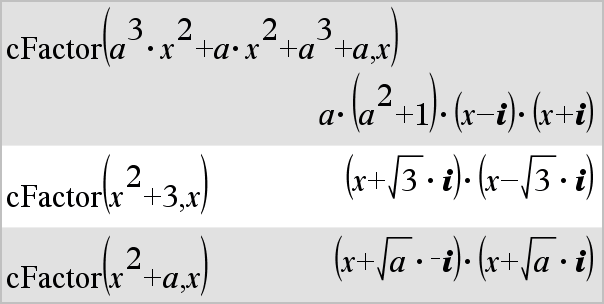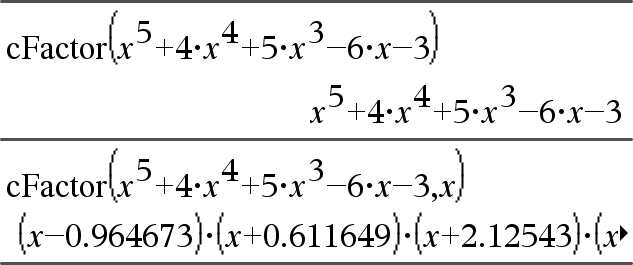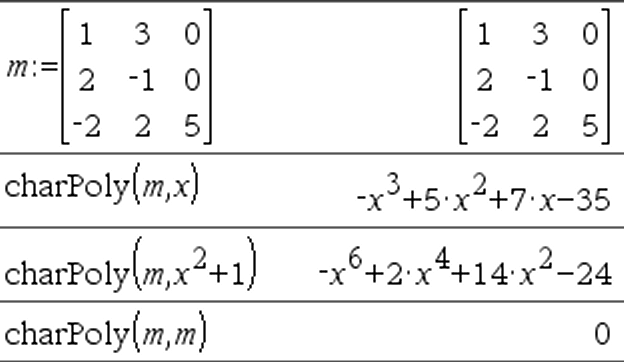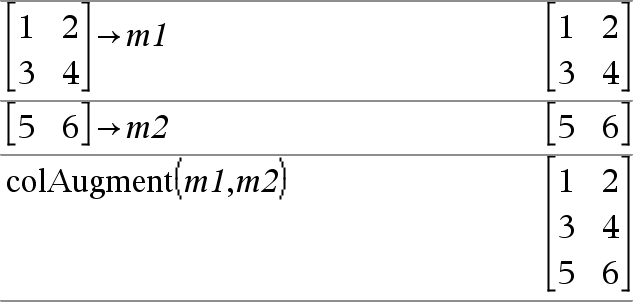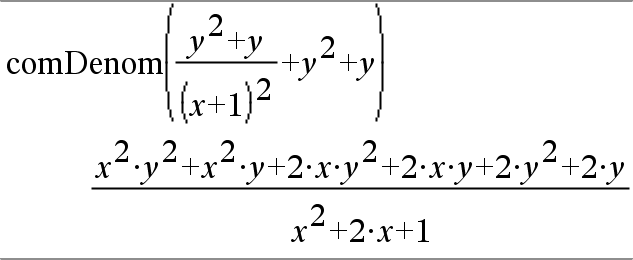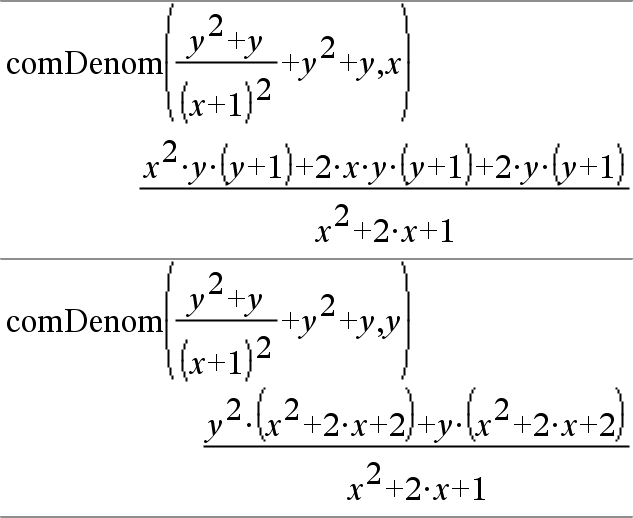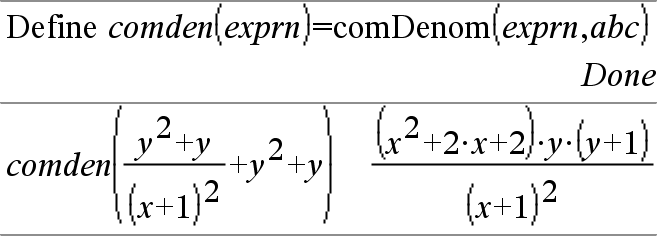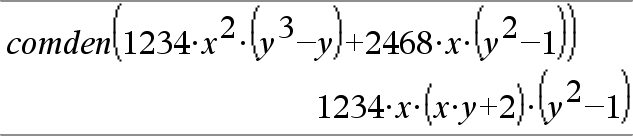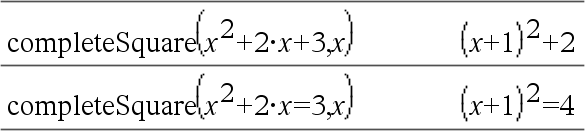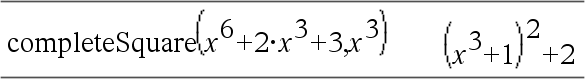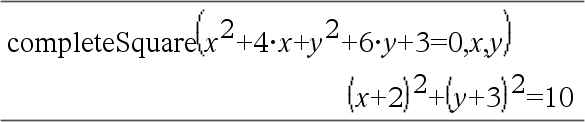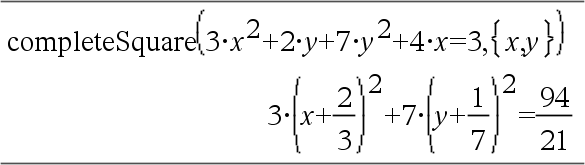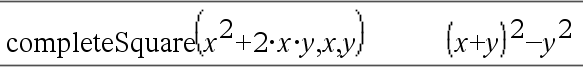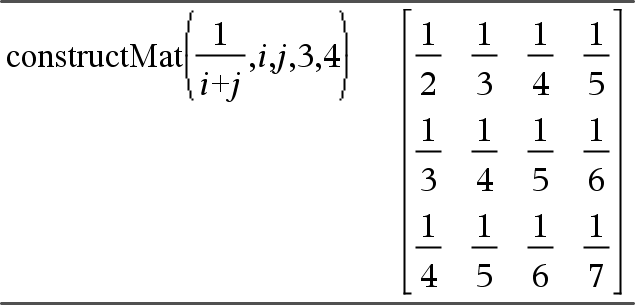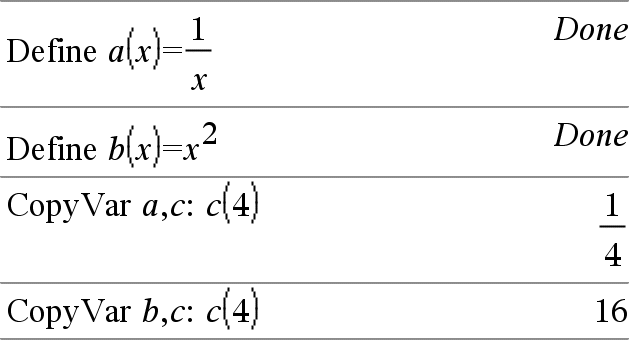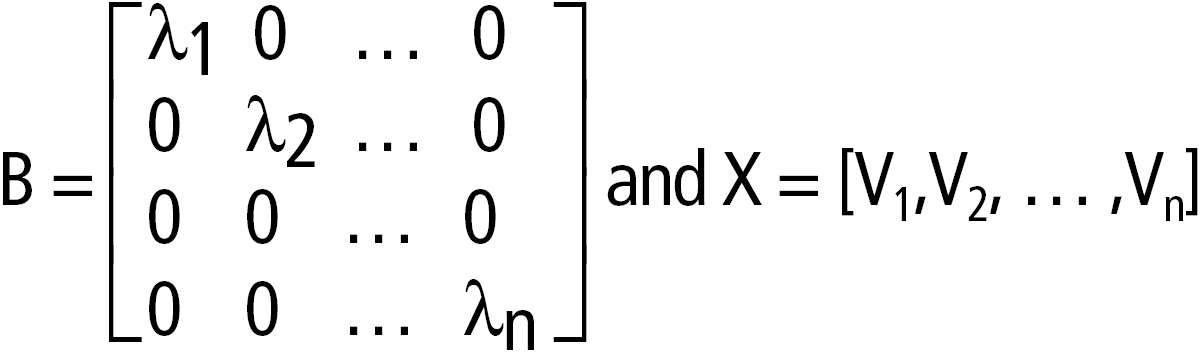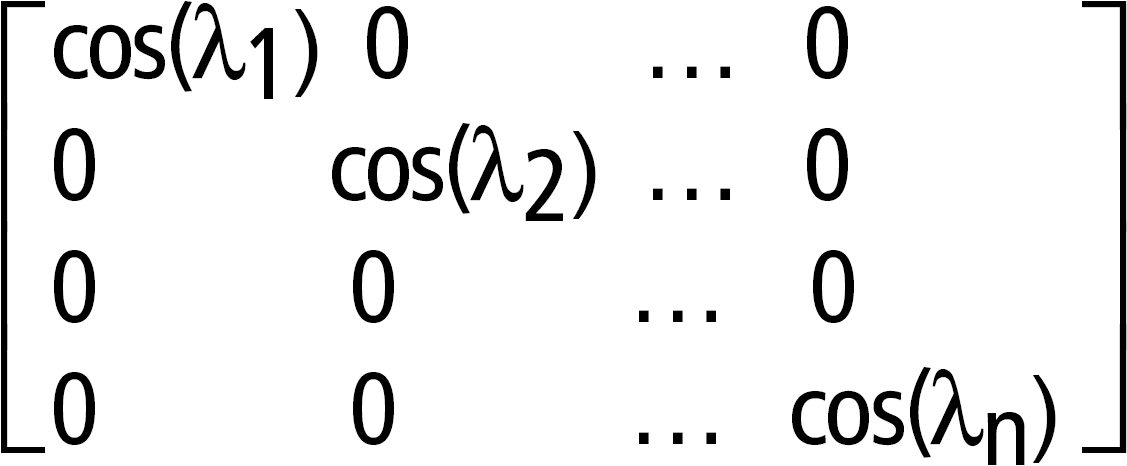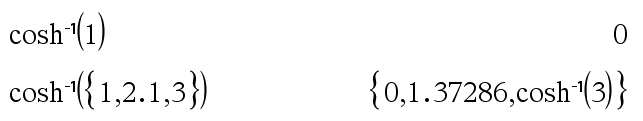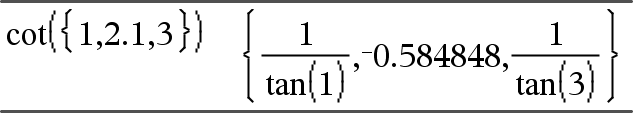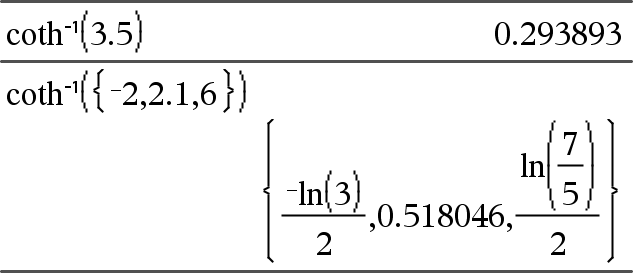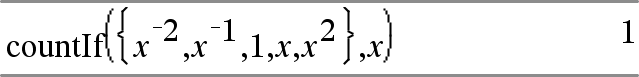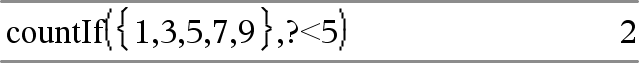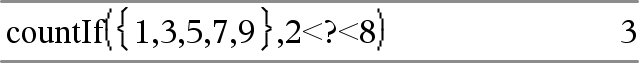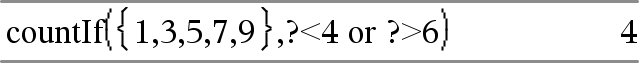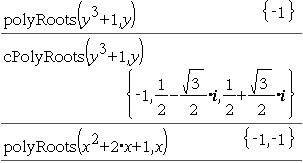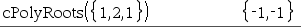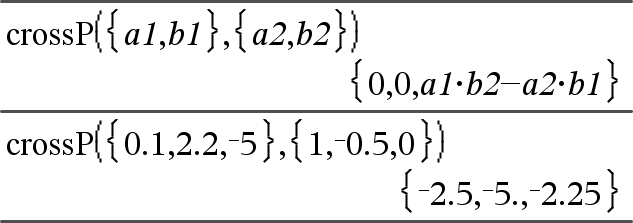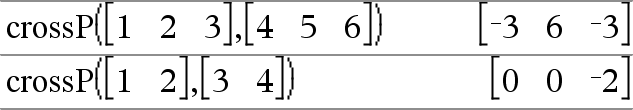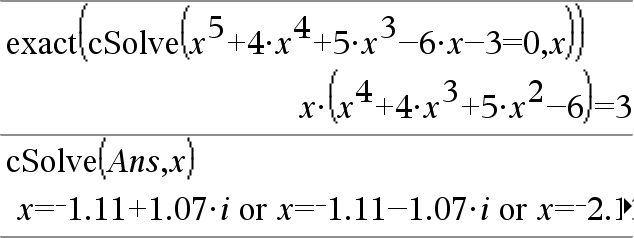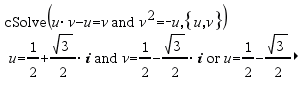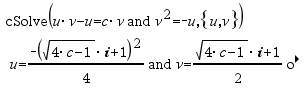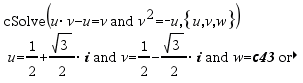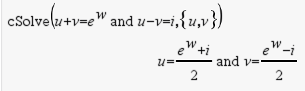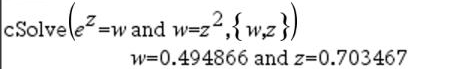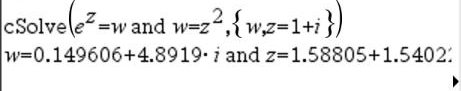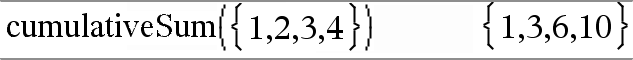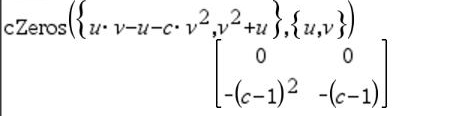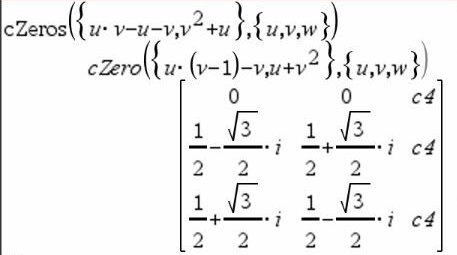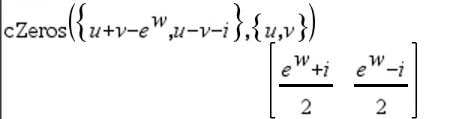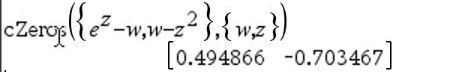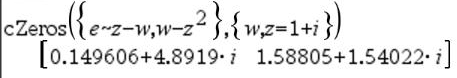|
Katalog > |
|
|
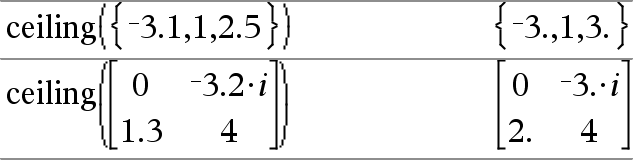
ceiling(Expr1)Þheltal Ger det närmaste heltal som är | argumentet. Argumentet kan vara ett reellt eller ett komplext tal. Obs: Se även floor(). |
|
|
ceiling(List1)Þlista ceiling(Matrix1)Þmatris Ger en lista eller matris över taket för varje element. |
|
|
Katalog > |
|
|
Ger den numeriska derivatan genom att använda formeln för symmetrisk differenskvot. När Värde specificeras överstyr detta värde eventuella tidigare variabeltilldelningar eller aktuella ersättningar av typ “|” för variabeln. Steg är stegvärdet. Om Steg utelämnas används förinställningen 0.001. När du använder Lista1 eller Matris1 utförs operationen på värdena i listan eller matriselementen. Obs: Se även avgRC() |
|
|
Katalog > |
|
|
cFactor(Expr1[,Var])Þuttryck cFactor(List1[,Var])Þlista cFactor(Matrix1[,Var])Þmatris
cFactor(Expr1) ger en faktorisering av Expr1 baserad på uttryckets alla variabler med en gemensam nämnare. Expr1 faktoriseras så långt det går till linjära, rationella faktorer även om detta inför nya icke-reella tal. Detta alternativ är lämpligt om du vill ha en faktorisering baserad på mer än en variabel. |
|
|
cFactor(Expr1,Var) ger en faktorisering av Expr1 baserad på variabeln Var. Expr1 faktoriseras så långt det går till faktorer som är linjära i Var, med kanske icke-reella konstanter, även om detta inför irrationella konstanter eller deluttryck som är irrationella i andra variabler. Faktorerna och deras termer sorteras med Var som huvudvariabel. Liknande potenser av Var samlas in i varje faktor. Inkludera Var om faktorisering baserad på endast denna variabel behövs och du är villig att acceptera irrationella uttryck i andra variabler för att öka faktoriseringen baserad på Var. Viss tillfällig faktorisering kan ske vad gäller andra variabler. |
|
|
Med inställningen Auto i läge Auto eller Ungefärlig medger inkludering av Var också en uppskattning med koefficienter med flytande decimalkomma när irrationella koefficienter inte explicit kan uttryckas kortfattat med termerna i de inbyggda funktionerna. Även med endast en variabel kan inkludering av Var ge en mer fullständig faktorisering. Obs: Se även faktor(). |
För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören. |
|
Katalog > |
|
|
char(Integer)Þtecken Ger en teckensträng som innehåller tecknet med numret Integer från handenhetens teckenuppsättning. Det giltiga området för Integer är 0–65535. |
|
|
Katalog > |
|
|
charPoly(squareMatrix,Var)Þpolynom charPoly(squareMatrix,Expr)Þpolynom charPoly(squareMatrix1,Matrix2)Þpolynom Ger det karakteristiska polynomet för squareMatrix. Det karakteristiska polynomet för n×n matris A, betecknat pA(l), är polynomet definierat av pA(l) = det(l• I NA) där I betecknar enhetsmatrisen n×n. squareMatrix1 och squareMatrix2 måste ha samma dimensioner. |
|
|
Katalog > |
|
|
c22way ObsMatrix chi22way ObsMatrix Beräknar ett c2-test för association på 2-vägstabellen över antal i den observerade matrisen ObsMatrix. En sammanfattning av resultaten visas i variabeln stat.results. (Se här.) För information om effekten av tomma element i en matris, se “Tomma element” (här). |
|
|
Resultatvariabel |
Beskrivning |
|
stat.c2 |
Chi-kvadratstatistik: summa (observerad - förväntad)2/förväntad |
|
stat.PVal |
Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas |
|
stat.df |
Frihetsgrader hos chi-kvadratstatistiken |
|
stat.ExpMat |
Matris över förväntad elementräknetabell, baserad på nollhypotesen |
|
stat.CompMat |
Matris över elementbidrag till chi-kvadratstatistiken |
|
Katalog > |
|
|
c2Cdf(lowBound,upBound,df)Þtal om lowBound och upBound är tal, lista om lowBound och upBound är listor chi2Cdf(lowBound,upBound,df)Þtal om lowBound och upBound är tal, lista om lowBound och upBound är listor Beräknar sannolikheten för c2-fördelning mellan lowBound och upBound för den specificerade frihetsgraden df. För P(X Å upBound), sätt lowBound = 0. För information om effekten av tomma element i en lista, se “Tomma element” (här). |
|
|
Katalog > |
|
|
c2GOF obsList,expList,df chi2GOF obsList,expList,df Utför ett test för att bekräfta att urvalsdata är från en population som följer en specificerad fördelning. obsList är en lista med data och måste innehålla heltal. En sammanfattning av resultaten visas i variabeln stat.results, här. För information om effekten av tomma element i en lista, se “Tomma element” (här). |
|
|
Resultatvariabel |
Beskrivning |
|
stat.c2 |
Chi-kvadratstatistik: summa (observerad - förväntad)2/förväntad |
|
stat.PVal |
Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas |
|
stat.df |
Frihetsgrader hos chi-kvadratstatistiken |
|
stat.CompList |
Elementbidrag till chi-kvadratstatistiken |
|
Katalog > |
|
|
c2Pdf(XVal,df)Þtal om XVal är ett tal, lista om XVal är en lista chi2Pdf(XVal,df)Þtal om XVal är ett tal, lista om XVal är en lista Beräknar värde hos täthetsfunktionen (pdf) för c2-fördelningen vid ett specificerat XVal-värde för den specificerade frihetsgraden df. För information om effekten av tomma element i en lista, se “Tomma element” (här). |
|
|
Katalog > |
|
|
ClearAZ Rensar alla variabler som har ett enda tecken i det aktuella problemet. Om en eller flera variabler är låsta visar detta kommando ett felmeddelande och tar endast bort olåsta variabler. Se |
|
|
Katalog > |
|
|
Rensar felstatusen och ställer in systemvariabeln errCode på noll. Villkoret Else i blocket Try...Else...EndTry bör använda ClrErr eller PassErr. Om felet skall processas eller ignoreras, använd ClrErr. Om det är okänt hur felet skall hanteras, använd PassErr för att skicka felet vidare till nästa felhanterare. Om det inte finns någon ytterligare felhanterare för Try...Else...EndTry visas feldialogrutan som normal. Obs: Se även PassErr, här och Try, här. Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
För ett exempel på ClrErr, se exempel 2 under kommandot Try, här.
|
|
Katalog > |
|
|
colAugment(Matrix1, Matrix2)Þmatris Ger en ny matris med Matrix2 fogad till Matrix1. Matriserna måste ha samma kolumndimensioner och Matrix2 fogas till Matrix1 som nya rader. Ändrar inte Matrix1 eller Matrix2. |
|
|
Katalog > |
|
|
colDim(Matrix)Þuttryck Ger antalet kolumner i Matrix. Obs: Se även rowDim(). |
|
|
Katalog > |
|
|
colNorm(Matrix)Þuttryck Ger maximum av summorna av absolutbeloppen på elementen i kolumnerna i Matrix. Obs: Odefinierade matriselement är ej tillåtna. Se även rowNorm(). |
|
|
Katalog > |
|
|
comDenom(Expr1[,Var])Þuttryck comDenom(List1[,Var])Þlista comDenom(Matrix1[,Var])Þmatris
comDenom(Expr1) ger en reducerad kvot mellan en fullt expanderad täljare och en fullt expanderad nämnare. |
|
|
comDenom(Expr1,Var) ger en reducerad kvot mellan täljare och nämnare som expanderats enligt Var. Termerna och deras faktorer sorteras med Var som huvudvariabel. Liknande potenser av Var samlas in. Viss tillfällig faktorisering kan ske av de insamlade koefficienterna. Jämfört med att utesluta Var sparar detta ofta tid, minne och skärmutrymme, vilket gör uttrycket mer begripligt. Det gör också att påföljande operationer på resultatet går snabbare och med mindre risk att minnet tar slut. |
|
|
Om Var inte förekommer i Expr1 ger comDenom(Expr1,Var) en reducerad kvot mellan en oexpanderad täljare och en oexpanderad nämnare. Sådana resultat sparar i regel ännu mer tid, minne och skärmutrymme. Sådana delvis faktoriserade resultat gör också att påföljande operationer på resultatet går mycket snabbare och med mycket mindre risk att minnet tar slut. |
|
|
Även om det inte finns någon nämnare är funktionen comden ofta ett snabbt sätt att erhålla en delvis faktorisering om factor() är för långsam eller om den utarmar minnet. Tips: Mata in denna comden() funktionsdefinition och prova den rutinmässigt som ett alternativ till comDenom() och factor(). |
|
|
Katalog > |
|
|
Konverterar ett kvadratiskt polynomuttryck på formen a·x2+b·x+c till formen a·(x-h)2+k – eller – Konverterar en andragradsekvation på formen a•x2+b•x+c=d till formen a·(x-h)2=k Det första argumentet måste vara ett kvadratiskt uttryck eller en andragradsekvation i standardform med avseende på det andra argumentet. Det andra argumentet måste vara en enda envariabelterm eller en enda envariabelterm upphöjd till en rationell potens, till exempel x, y2 eller z(1/3). Den tredje och fjärde syntaxen försöker att fullborda kvadraten avseende variablerna Var1, Var2 [,… ]). |
|
|
Katalog > |
|
|
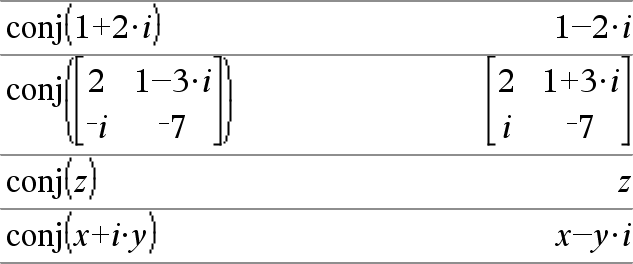
conj(Expr1)Þuttryck conj(List1)Þlista conj(Matrix1)Þmatris Ger argumentets komplexkonjugat. Obs: Alla odefinierade variabler behandlas som reella variabler. |
|
|
Katalog > |
|
|
constructMat(Expr,Var1,Var2,numRows,numCols) Þmatris Ger en matris baserad på argumenten. Expr är ett uttryck i variablerna Var1 och Var2. Element i den resulterande matrisen skapas genom att utvärdera Expr för varje ökat värde på Var1 och Var2. Var1 ökas automatiskt från 1 till och med numRows. Inom varje rad ökas Var2 från 1 till och med numCols. |
|
|
Katalog > |
|
|
CopyVar Var1, Var2 CopyVar Var1., Var2. CopyVar Var1, Var2 kopierar värdet på variabel Var1 till variabel Var2, och skapar Var2 vid behov. Variabeln Var1 måste ha ett värde. Om Var1 är namnet på en befintlig användardefinierad funktion kopieras definitionen på denna funktion till funktionen Var2. Funktionen Var1 måste vara definierad. Var1 måste uppfylla kraven för namngivning av variabler eller måste vara ett indirection-uttryck som förenklas till ett variabelnamn som uppfyller kraven. |
|
|
CopyVar Var1., Var2. kopierar alla led i variabelgruppen Var1. till gruppen Var2. och skapar Var2. vid behov. Var1. måste vara namnet på en befintlig variabelgrupp, till exempel, den statistiska stat.nn-resultat eller variabler skapade med funktionen |
|
|
Katalog > |
|
|
corrMat(List1,List2[,…[,List20]]) Beräknar korrelationsmatrisen för den sammanfogade matrisen [List1, List2, ..., List20]. |
|
|
Katalog > |
|
|
Expr 4cos Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>cos. Representerar Expr i termer av cosinus. Detta är en omvandlingsoperator för visning. Den kan endast användas i slutet av inmatningsraden. 4cos reducerar alla potenser av sin(...) modulo 1Ncos(...)^2 så att eventuella återstående potenser av cos(...) har exponenter i området (0, 2). Resultatet kommer sålunda att vara fritt från sin(...) om, och endast om, sin(...) finns i det givna uttrycket vid jämna potenser. Obs: Denna omvandlingsoperator stöds inte i vinkellägena Grader och Nygrader. Innan du använder den, kontrollera att vinkelläget är inställt på Radianer och att Expr inte innehåller explicita referenser till vinklar i grader eller nygrader. |
|
|
µ tangent |
|
|
cos(Expr1)Þuttryck cos(List1)Þlista
cos(List1) ger en lista på cosinus för alla element i List1. Obs: Argumentet tolkas som en vinkel i grader, nygrader eller radianer enligt det inställda vinkelläget. Du kan använda ¡, G eller R för att tillfälligt överstyra vinkelläget. |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
cos(squareMatrix1)ÞkvadratMatris Ger matrisen med cosinus för squareMatrix1. Detta är inte detsamma som att beräkna cosinus för varje element. När en skalär funktion f(A) används på squareMatrix1 (A) beräknas resultatet med algoritmen: Beräkna egenvärdena (li) och egenvektorerna (Vi) för A. squareMatrix1 måste vara möjlig att diagonalisera. Den får inte heller ha symboliska variabler som inte har tilldelats ett värde. Forma matriserna:
Då är A = X B X/och f(A) = X f(B) X/. Exempelvis cos(A) = X cos(B) X/ där: cos(B) =
Alla beräkningar utförs med flyttalsaritmetik. |
I vinkelläget Radianer:
|
|
µ tangent |
|
|
cos/(Expr1)Þuttryck cos/(List1)Þlista
cos/(List1) ger en lista på invers cosinus för varje element i List1. Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer beroende på det aktuella vinkelläget. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccos(...). |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
cos/(squareMatrix1)ÞsquareMatrix Ger matrisen med invers cosinus för squareMatrix1. Detta är inte detsamma som att beräkna invers cosinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer och i Rektangulärt komplext format:
För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören. |
|
Katalog > |
|
|
cosh(Expr1)Þuttryck cosh(List1)Þlista
cosh(List1) ger en lista på hyperbolisk cosinus för varje element i List1. |
I vinkelläget Grader:
|
|
cosh(squareMatrix1)ÞkvadratMatris Ger matrisen med hyperbolisk cosinus för squareMatrix1. Detta är inte detsamma som att beräkna hyperbolisk cosinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer:
|
|
Katalog > |
|
|
cosh/(Expr1)Þuttryck cosh/(List1)Þlista
cosh/(List1) ger en lista på invers hyperbolisk cosinus för varje element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccosh(...). |
|
|
cosh/(squareMatrix1)ÞkvadratMatris Ger matrisen med invers hyperbolisk cosinus för squareMatrix1. Detta är inte detsamma som att beräkna invers hyperbolisk cosinus för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
I vinkelläget Radianer och i Rektangulärt komplext format:
För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören. |
|
µ tangent |
|
|
cot(Expr1) Þ uttryck cot(List1) Þ lista Ger cotangens för Expr1 eller en lista på cotangens för alla element i List1. Obs: Argumentet tolkas som en vinkel i grader, nygrader eller radianer enligt det inställda vinkelläget. Du kan använda ¡, G eller R för att tillfälligt överstyra vinkelläget. |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
µ tangent |
|
|
cot/(Expr1)Þuttryck cot/(List1)Þlista Ger den vinkel vars cotangens är Expr1 eller en lista på invers cotangens för varje element i List1. Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer beroende på det aktuella vinkelläget. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccot(...). |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
Katalog > |
|
|
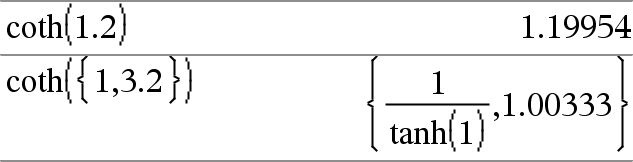
coth(Expr1)Þuttryck coth(List1)Þlista Ger hyperbolisk cotangens för Expr1 eller en lista på hyperbolisk cotangens för alla element i List1. |
|
|
Katalog > |
|
|
coth/(Expr1)Þuttryck coth/(List1)Þlista Ger den inversa hyperboliska cotangensen för Expr1 eller en lista på invers hyperbolisk cotangens för alla element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccoth(...). |
|
|
Katalog > |
|
|
count(Value1orList1 [,Value2orList2 [,...]])Þvärde Ger det totala ackumulerade antalet element i argumenten som utvärderas till numeriska värden. Varje argument kan vara ett uttryck, ett värde, en lista eller en matris. Du kan blanda datatyper och använda argument med olika dimensioner. För en lista, en matris, eller ett område av celler, utvärderas varje element för att bestämma om det skall inkluderas i räkningen. I applikationen Listor och kalkylblad kan du använda ett område av celler i stället för ett argument. Tomma element ignoreras. För mer information om tomma element, se här. |
I det sista exemplet räknas endast 1/2 och 3+4*i. De återstående argumenten, förutsatt att x är odefinierad, utvärderas inte till numeriska värden. |
|
Katalog > |
|||||||
|
countif(List,Criteria)Þvärde Ger det totala ackumulerade antalet element i List som uppfyller specificerade Criteria. Criteria kan vara:
I applikationen Listor och kalkylblad kan du använda ett område av celler i stället för List. Tomma element i listan ignoreras. För mer information om tomma element, se här. |
Räknar antalet element som är lika med 3.
Räknar antalet element som är lika med “def.”
Räknar antalet element som är lika med x. I detta exempel förutsätts att variabeln x är odefinierad.
Räknar 1 och 3.
Räknar 3, 5 och 7.
Räknar 1, 3, 7 och 9. |
|
Katalog > |
|
|
Den första syntaxen,
Den andra syntaxen, Obs: Se även |
|
|
Katalog > |
|
|
crossP(List1, List2)Þlista Ger vektorprodukten av List1 och List2 som en lista. List1 och List2 måste ha samma dimension och dimensionen måste vara antingen 2 eller 3. |
|
|
crossP(Vector1, Vector2)Þvektor Ger en rad- eller kolumnvektor (beroende på argumenten) som är vektorprodukten av Vector1 och Vector2. Både Vector1 och Vector2 måste vara radvektorer eller båda måste vara kolumnvektorer. Båda vektorerna måste ha samma dimension och dimensionen måste vara antingen 2 eller 3. |
|
|
µ tangent |
|
|
csc(Expr1)Þuttryck csc(List1)Þlista Ger cosekanten för Expr1 eller en lista på cosekanten för alla element i List1. |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
µ tangent |
|
|
csc/(Expr1) Þ uttryck csc/(List1) Þ lista Ger den vinkel vars cosekant är Expr1 eller en lista på den inversa cosekanten för varje element i List1. Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer beroende på det aktuella vinkelläget. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccsc(...). |
I vinkelläget Grader:
I vinkelläget Nygrader:
I vinkelläget Radianer:
|
|
Katalog > |
|
|
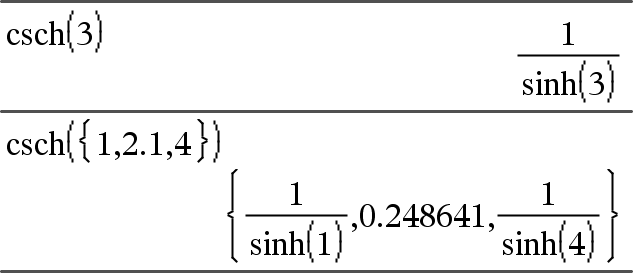
csch(Expr1) Þ uttryck csch(List1) Þ lista Ger den hyperboliska cosekanten för Expr1 eller en lista på den hyperboliska cosekanten för alla element i List1. |
|
|
Katalog > |
|
|
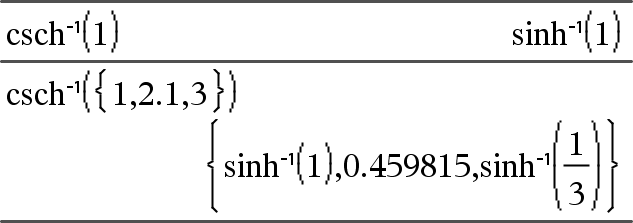
csch/(Expr1) Þ uttryck csch/(List1) Þ lista Ger den inversa hyperboliska cosekanten för Expr1 eller en lista på den inversa hyperboliska cosekanten för alla element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva arccsch(...). |
|
|
Katalog > |
|
|
CubicReg X, Y[, [Freq] [, Category, Include]] Utför en tredjegrads regressionsanalysy = a·x3+b· x2+c·x+dpå listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results, här. Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0. Category är en lista på kategorikoder för motsvarande X- och Y-data. Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen. För information om effekten av tomma element i en lista, se “Tomma element” (här). |
|
|
Resultatvariabel |
Beskrivning |
|
stat.RegEqn |
Regressionsekvation: a·x3+b·x2+c·x+d |
|
stat.a, stat.b, stat.c, stat.d |
Regressionskoefficienter |
|
stat.R2 |
Determinationskoefficient |
|
stat.Resid |
Residualer från regressionsanalysen |
|
stat.XReg |
Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i Freq, Category List och Include Categories |
|
stat.YReg |
Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i Freq, Category List och Include Categories |
|
stat.FreqReg |
Lista på frekvenser som motsvarar stat.XReg och stat.YReg |
|
Katalog > |
|
|
cumulativeSum(List1)Þlista Ger en lista på de kumulativa summorna av elementen i List1 och börjar med element 1. |
|
|
cumulativeSum(Matrix1)Þmatris Ger en matris över de kumulativa summorna av elementen i Matrix1. Varje element är den kumulativa summan i kolumnen räknat uppifrån och ned. Ett tomt element i List1 eller Matrix1 ger ett tomt element i den resulterande listan eller matrisen. För mer information om tomma element, se här. |
|
|
Katalog > |
|
|
Cycle Överför omedelbart kontroll till nästa iteration i den aktuella slingan (For, While eller Loop). Cycle tillåts inte utanför de tre slingstrukturerna (For, While eller Loop). Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
Funktion som listar heltal från 1 till 100 utom 50.
|
|
Katalog > |
|
|
Vector 4Cylind Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @>Cylind. Visar rad- eller kolumnvektorn i cylindrisk form [r,±q, z]. Vector måste ha exakt tre element. Den kan vara antingen en rad eller en kolumn. |
|