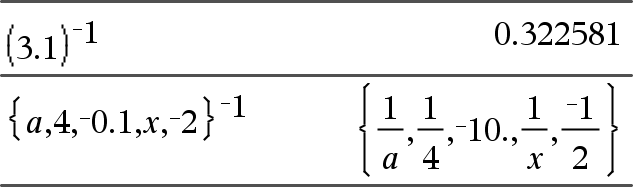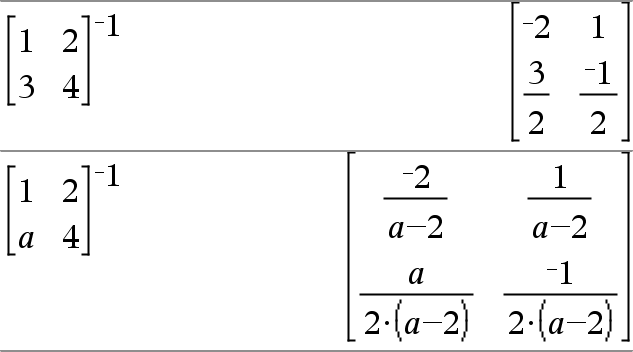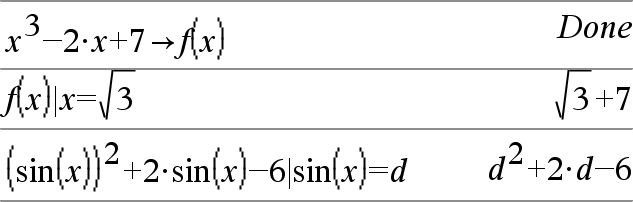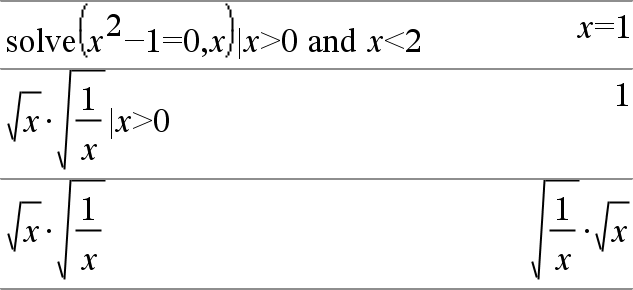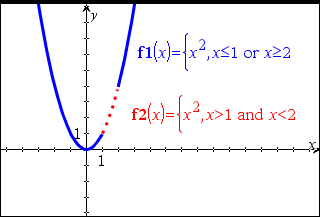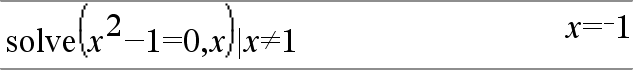|
+tangent |
|
|
Ger summan av de två argumenten. |
|
|
List1 + List2Þlista Matrix1 + Matrix2Þmatris Ger en lista (eller matris) som innehåller summorna av motsvarande element i List1 och List2 (eller Matrix1 och Matrix2). Argumenten måste ha samma dimensioner. |
|
|
List1 + ExprÞlista Ger en lista på summorna av Expr och varje element i List1. |
|
|
Matrix1 + ExprÞmatris Ger en matris med Expr adderat till varje element i diagonalen av Matrix1. Matrix1 måste vara kvadratisk. Obs: Använd .+ (punkt plus) för att lägga till ett uttryck till varje element. |
|
|
-tangent |
|
|
Ger Expr1 minus Expr2. |
|
|
List1 N List2Þlista Matrix1 N Matrix2Þmatris Subtraherar varje element i List2 (eller Matrix2) från motsvarande element i List1 (eller Matrix1) och ger resultatet. Argumenten måste ha samma dimensioner. |
|
|
List1 N ExprÞlista Subtraherar varje element i List1 från Expr eller subtraherar Expr från varje element i List1 och ger en lista på resultaten. |
|
|
Matrix1 N ExprÞmatris Expr N Matrix1 ger en matris över Expr gånger enhetsmatrisen minus Matrix1. Matrix1 måste vara kvadratisk. Matrix1 N Expr ger en matris över Expr gånger enhetsmatrisen subtraherad från Matrix1. Matrix1 måste vara kvadratisk. Obs: Använd .N (punkt minus) för att subtrahera ett uttryck från varje element. |
|
|
rtangent |
|
|
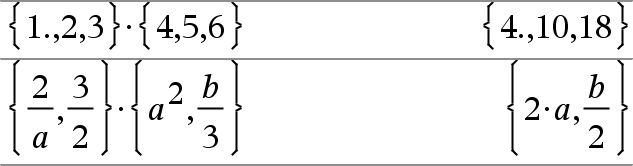
Ger produkten av de två argumenten. |
|
|
List1·List2Þlista Ger en lista som innehåller produkterna av motsvarande element i List1 och List2. Listorna måste ha samma dimensioner. |
|
|
Matrix1 ·Matrix2Þmatris Ger en matris över produkten av Matrix1 och Matrix2. Antalet kolumner i Matrix1 måste vara lika med antalet rader i Matrix2. |
|
|
List1 ·ExprÞlista Ger en lista på produkterna av Expr och varje element i List1. |
|
|
Matrix1 ·ExprÞmatris Ger en matris över produkterna av Expr och varje element i Matrix1. Obs: Använd .·(punkt multiplicera) för att multiplicera ett uttryck med varje element. |
|
|
ptangent |
|
|
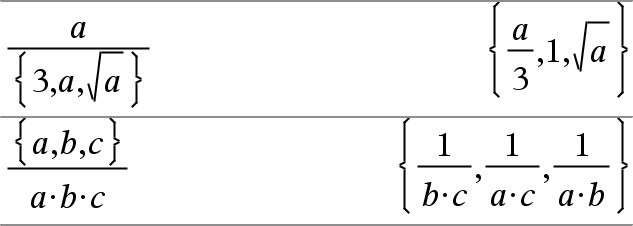
Expr1 àExpr2Þuttryck Ger kvoten av Expr1 dividerat med Expr2. Obs: Se även Fraction template, här. |
|
|
List1 à List2Þlista Ger en lista på kvoterna av List1 dividerat med List2. Listorna måste ha samma dimensioner. |
|
|
List1 à Expr Þ lista Ger en lista på kvoterna av Expr dividerat med List1 ellerList1 dividerat med Expr. |
|
|
Ger en matris över kvoterna av Matrix1àExpr. Obs: Använd . / (punkt dividera) för att dividera ett uttryck med varje element. |
|
|
ltangent |
|
|
List1 ^ List2 Þ lista Ger det första argumentet upphöjt till det andra argumentets potens. Obs: Se även Exponent template, här. Ger, för en lista, elementen i List1 upphöjda till potensen för motsvarande element i List2. I det reella området använder potenser i bråkform som har reducerade exponenter med udda nämnare den reella delen kontra principaldelen för komplext läge. |
|
|
Ger Expr upphöjt till potensen för elementen i List1. |
|
|
Ger elementen i List1 upphöjda till potensen för Expr. |
|
|
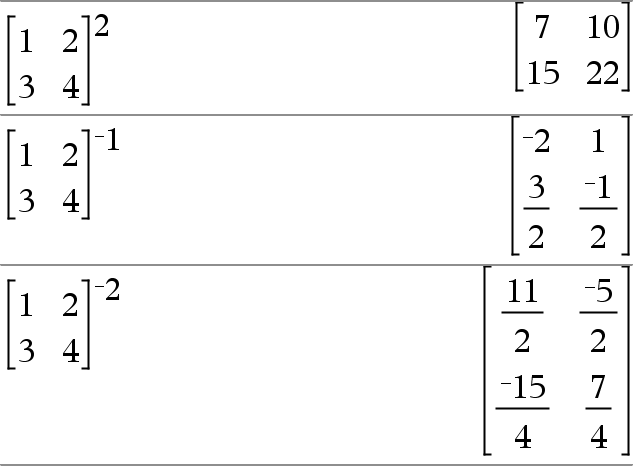
squareMatrix1 ^ integer Þ matris Ger squareMatrix1 upphöjd till potensen för integer (heltal). squareMatrix1 måste vara en kvadratisk matris. Om integer = L1 beräknas den inversa matrisen. Om integer < L1 beräknas den inversa matrisen till en lämplig positiv potens. |
|
|
q tangent |
|
|
Ger kvadraten på argumentet. List12 Þ lista Ger en lista med kvadraterna på elementen i List1. squareMatrix12 Þ matris Ger en matris över kvadraten på squareMatrix1. Detta är inte detsamma som att beräkna kvadraten på varje element. Använd .^2 för att beräkna kvadraten på varje element. |
|
|
^+ tangenter |
|
|
Matrix1 .+ Matrix2 Þ matris
Matrix1 .+ Matrix2 ger en matris som är summan av varje par av motsvarande element i Matrix1 och Matrix2.
|
|
|
^- tangenter |
|
|
Matrix1 .N Matrix2 Þ matrixs Matrix1 .NMatrix2 ger en matris som är skillnaden mellan varje par av motsvarande element i Matrix1 och Matrix2.
|
|
|
^r tangenter |
|
|
Matrix1 .· Matrix2 Þ matris
Matrix1 .· Matrix2 ger en matris som är produkten av varje par av motsvarande element i Matrix1 och Matrix2.
|
|
|
^p tangenter |
|
|
Matrix1 . / Matrix2 Þ matris
Matrix1 . / Matrix2 ger en matris som är kvoten av varje par av motsvarande element i Matrix1 och Matrix2.
|
|
|
^l tangenter |
|
|
Matrix1 .^ Matrix2 Þ matris Matrix1 .^ Matrix2 ger en matris där varje element i Matrix2 är exponenten för motsvarande element i Matrix1.
|
|
|
v tangent |
|
|
LList1 Þ lista LMatrix1 Þ matris Ger argumentets negation. Ger, för en lista eller matris, alla elementen negerade. Om argumentet är ett binärt eller hexadecimalt heltal ger negationen tvåkomplementet. |
I binärt basläge: Viktigt: Noll, inte bokstaven O.
För att se hela resultatet, tryck på 5 och använd sedan 7 och 8 för att flytta markören. |
|
/k tangenter |
|
|
List1 % Þ lista Matrix1 % Þ matris Ger Ger, för en lista eller matris, en lista eller matris med varje element dividerat med 100. |
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
|
|
= tangent |
|
|
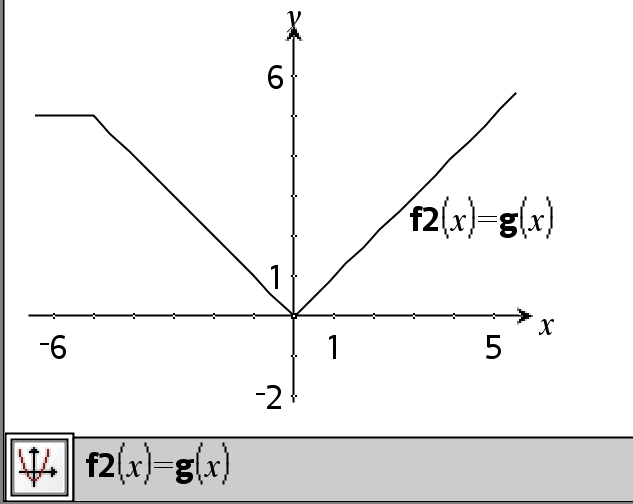
Expr1 = Expr2ÞBooleskt uttryck List1 = List2Þ Boolesk lista Matrix1 = Matrix2Þ Boolesk matris Ger resultatet sant om Expr1 bestäms vara lika med Expr2. Ger resultatet falskt om Expr1 bestäms inte vara lika med Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
Exempel på funktion som använder matchande testsymboler: =, ƒ, <, {, >, |
Resultat från plottning av g(x)
|
|
/= tangenter |
|
|
Expr1 ƒ Expr2 Þ Booleskt uttryck List1 ƒ List2 Þ Boolesk lista Matrix1 ƒ Matrix2 Þ Boolesk matris Ger resultatet sant om Expr1 bestäms inte vara lika med Expr2. Ger resultatet falskt om Expr1 bestäms vara lika med Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva /= |
Se exemplet “=” (lika med). |
|
/= tangenter |
|
|
Expr1 < Expr2 Þ Booleskt uttryck List1 < List2 Þ Boolesk lista Matrix1 < Matrix2 Þ Boolesk matris Ger resultatet sant om Expr1 bestäms vara mindre än Expr2. Ger resultatet falskt om Expr1 bestäms vara större än eller lika med Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. |
Se exemplet “=” (lika med). |
|
/= tangenter |
|
|
Expr1 { Expr2 Þ Booleskt uttryck List1 { List2 Þ Boolesk lista Matrix1 { Matrix2 Þ Boolesk matris Ger resultatet sant om Expr1 bestäms vara mindre än eller lika med Expr2. Ger resultatet falskt om Expr1 bestäms vara större än Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva <= |
Se exemplet “=” (lika med). |
|
/= tangenter |
|
|
Expr1 > Expr2 Þ Booleskt uttryck List1 > List2 Þ Boolesk lista Matrix1 > Matrix2 Þ Boolesk matris Ger resultatet sant om Expr1 bestäms vara större än Expr2. Ger resultatet falskt om Expr1 bestäms vara mindre än eller lika med Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. |
Se exemplet “=” (lika med). |
|
/= tangenter |
|
|
Expr1 | Expr2 Þ Booleskt uttryck List1 | List2 Þ Boolesk lista Matrix1 | Matrix2 Þ Boolesk matris Ger resultatet falskt om Expr1 bestäms vara större än eller lika med Expr2. Ger resultatet falskt om Expr1 bestäms vara mindre än Expr2. Allt annat ger en förenklad form av ekvationen. Ger, för listor och matriser, jämförelser element för element. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva >= |
Se exemplet “=” (lika med). |
|
/= knappar |
|
|
BoolesktUttr1 Þ BoolesktUttr2 ger Booleskt uttryck BooleskLista1 Þ BooleskLista2 ger Boolesk lista BooleskMatris1 Þ BooleskMatris2 ger Boolesk matris Heltal1 Þ Heltal2 ger Heltal
Beräknar uttrycket Ger, för listor och matriser, jämförelser element för element. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva => |
|
|
/= knappar |
|
|
BoolesktUttr1 Û BoolesktUttr2 ger Booleskt uttryck BooleskLista1 Û BooleskLista2 ger Boolesk lista BooleskMatris1 Û BooleskMatris2 ger Boolesk matris Heltal1 Û Heltal2 ger Heltal
Ger negation av en Ger, för listor och matriser, jämförelser element för element. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva <=> |
|
|
º tangent |
|
|
List1! Þ lista Matrix1! Þ matris Ger argumentets fakultet. Ger, för en lista eller matris, en lista eller matris med elementens fakulteter. |
|
|
/k tangenter |
|
|
String1 & String2 Þ sträng Ger en textsträng som är String2 bifogad till String1. |
|
|
Katalog > |
||||||||||
|
d(Uttr1, Var[, Ordning])Þuttryck d(Lista1, Var[, Ordning])Þlista d(Matris1, Var[, Ordning])Þmatris Ger förstaderivatan av det första argumentet med avseende på variabeln Var. Ordning, om inkluderad, måste vara ett heltal. Om ordningen är mindre än noll blir resultatet en antiderivata. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva
|
|
|
Katalog > |
|
|
‰(Uttr1, Var[, Undre, Övre]) Þ uttryck ‰(Uttr1, Var[, Konstant]) Þ uttryck Ger integralen av Uttr1 med avseende på Var från Undre till Övre. Obs: Se även Mall för bestämd integral eller Mall för obestämd integral, här. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva integral(...). |
|
|
Om Lower och Upper utelämnas erhålls en primitiv funktion. En symbolisk integrationskonstant utelämnas såvida du inte anger argumentet Constant. |
|
|
Jämbördigt giltiga antiderivator kan skilja med en numerisk konstant. En sådan konstant kan vara maskerad, särskilt när en antiderivata innehåller logaritmer eller inversa trigonometriska funktioner. Dessutom läggs ibland stegvisa konstanta uttryck till för att göra en antiderivata giltig över ett större intervall än med den vanliga formeln. |
|
|
‰() returnerar sig själv för steg av Expr1 som inte kan bestämmas som en explicit ändlig kombination av dess inbyggda funktioner och operatorer. När du anger Lower och Upper görs ett försök att hitta eventuella diskontinuiteter eller diskontinuerliga derivator i intervallet Lower < Var < Upper för att dela upp intervallet vid dessa ställen. |
|
|
Med inställningen Auto i läge Auto eller Ungefärlig används numerisk integrering där så är tillämpligt när en antiderivata eller ett gränsvärde inte kan bestämmas. |
|
|
Med inställningen Approximate görs först ett försök med numerisk integrering om detta är tillämpligt. Antiderivata söks endast där sådan numerisk integrering inte är tillämplig eller misslyckas. |
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
|
|
‰() kan kapslas in för att göra multipelintegraler. Integrationsgränser kan bero på integrationsvariabler utanför gränserna.
|
|
|
/q tangenter |
|
|
‡ (List1)Þlista Ger kvadratroten ur argumentet. Ger, för en lista, kvadratrötterna ur alla element i List1. Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva sqrt(...) Obs: Se även Square root template, här. |
|
|
Katalog > |
|
|
P(Expr1, Var, Low, High)Þuttryck Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva prodSeq(...). Utvärderar Expr1 för varje värde på Var från Low till High och ger produkten av resultaten. Obs: Se även Product template (P), här. |
|
|
P(Expr1, Var, Low, LowN1)Þ1 P(Expr1, Var, Low, High) Þ1/P(Expr1, Var, High+1, LowN1) om High < LowN1 Produktformlerna som används har härletts från följande referens: Ronald L. Graham, Donald E. Knuth och Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalog > |
|
|
G(Expr1, Var, Low, High)Þuttryck Obs: Du kan infoga denna funktion med datorns tangentbord genom att skriva sumSeq(...). Utvärderar Uttr1 för varje värde på Var från Låg till Hög och ger summan av resultaten. Obs: Se även Sum template, här. |
|
|
G(Expr1, Var, Low, LowN1)Þ0 G(Expr1, Var, Low, High) ÞLG(Expr1, Var, High+1, LowN1) om High < LowN1
Summaformlerna som används har härletts från följande referens: Ronald L. Graham, Donald E. Knuth och Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalog > |
||||||||||
|
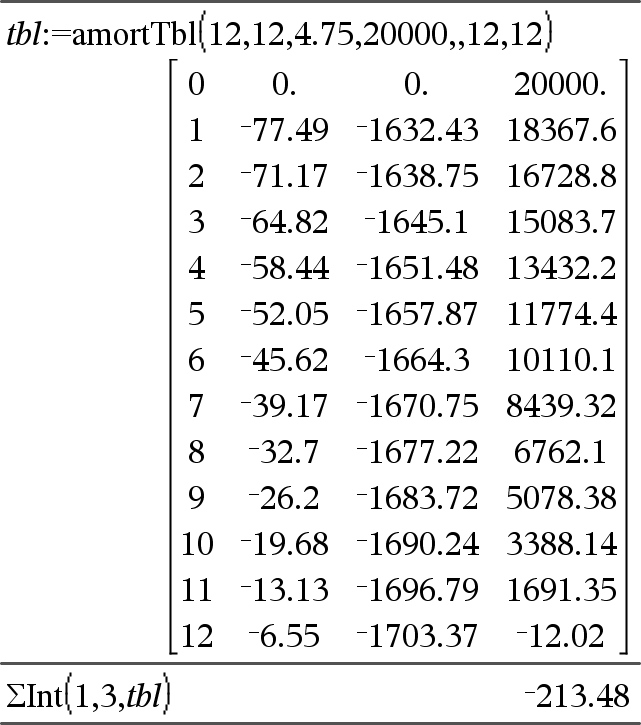
GInt(NPmt1, NPmt2, N, I, PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue])Þvärde GInt(NPmt1,NPmt2,amortTable)Þvärde Amorteringsfunktion som beräknar räntesumman under ett specificerat område av betalningar. NPmt1 och NPmt2 definierar start och slut på betalningsområdet. N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se här.
roundValue anger antalet decimaler för avrundning. Förinställning: 2. GInt(NPmt1,NPmt2,amortTable) beräknar räntesumman baserat på amorteringstabellen amortTable. Argumentet amortTable måste vara en matris i den form som beskrivs under amortTbl(), här. Obs: Se även GPrn() nedan och Bal(), här. |
|
|
Katalog > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue])Þvärde GPrn(NPmt1,NPmt2,amortTable)Þvärde Amorteringsfunktion som beräknar kapitalsumman under ett specificerat område av betalningar. NPmt1 och NPmt2 definierar start och slut på betalningsområdet. N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se här.
roundValue anger antalet decimaler för avrundning. Förinställning: 2. GPrn(NPmt1,NPmt2,amortTable) beräknar summan av betalt kapital baserat på amorteringstabellen amortTable. Argumentet amortTable måste vara en matris i den form som beskrivs under amortTbl(), här. Obs: Se även GInt() ovan och Bal(), här. |
|
|
/k tangenter |
|
|
# varNameString Avser variabeln vars namn är varNameString. Detta låter dig använda strängar för att skapa variabelnamn inom en funktion. |
Skapar eller avser variabeln xyz.
Ger värdet på variabeln (r) vars namn är lagrat i variabeln s1. |
|
i tangent |
|
|
mantissaEexponent Skriver in ett tal i grundpotensform. Talet tolkas som mantissa × 10exponent. Tips: Om du vill skriva in en potens av 10 utan att orsaka ett decimalt resultat, använd 10^integer. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva @E. Skriv exempelvis 2.3@E4 för att mata in 2.3E4. |
|
|
1 tangent |
|
|
List1gÞlista Matrix1gÞmatris Denna funktion ger dig ett sätt att specificera en vinkel i nygrader när du är i läge Grader eller Radianer. Multiplicerar i vinkelläget Radianer Expr1 med p/200. Multiplicerar i vinkelläget Grader Expr1 med g/100. Ger i läget Nygrader Expr1 oförändrat. Obs: Du kan infoga denna symbol med datorns tangentbord genom att skriva @g. |
I vinkelläge Grader, Nygrader eller Radianer:
|
|
1 tangent |
|
|
List1R Þlista Matrix1R Þmatris Denna funktion ger dig ett sätt att specificera en vinkel i radianer när du är i läge Grader eller Nygrader. Multiplicerar i vinkelläget Grader argumentet med 180/p. Ger i vinkelläget Radianer argumentet oförändrat. Multiplicerar i vinkelläget Nygrader argumentet med 200/p. Tips: Använd R om du vill framtvinga radianer i en funktionsdefinition oavsett det inställda läget när funktionen används. Obs: Du kan infoga denna symbol med datorns tangentbord genom att skriva @r. |
I vinkelläge Grader, Nygrader eller Radianer:
|
|
1 tangent |
|
|
List1¡Þlista Matrix1¡Þmatris Denna funktion ger dig ett sätt att specificera en vinkel i grader när du är i läge Nygrader eller Radianer. Multiplicerar i vinkelläget Radianer argumentet med p/180. Ger i vinkelläget Grader argumentet oförändrat. Multiplicerar i vinkelläget Nygrader argumentet med 10/9. Obs: Du kan infoga denna symbol med datorns tangentbord genom att skriva @d. |
I vinkelläge Grader, Nygrader eller Radianer:
I vinkelläget Radianer: Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
|
|
/k tangenter |
|||||||
|
dd¡mm'ss.ss''Þuttryck ddEtt positivt eller negativt tal mmEtt icke negativt tal ss.ssEtt icke negativt tal Ger dd+(mm/60)+(ss.ss/3600). Med detta bas‑60 inmatningsformat kan du:
Obs: Avsluta ss.ss med två apostrofer (''), inte med citationstecken ("). |
I vinkelläget Grader:
|
|
/k tangenter |
|
|
[Radius,±q_Angle]Þvektor (polär indata) [Radius,±q_Angle,Z_Coordinate]Þvektor (cylindrisk indata) [Radius,±q_Angle,±q_Angle]Þvektor (sfärisk indata) Ger koordinater som en vektor beroende på det inställda vektorformatläget: rektangulär, cylindrisk eller sfärisk. Obs: Du kan infoga denna symbol med datorns tangentbord genom att skriva @<. |
I vinkelläget Radianer och med vektorformatet inställt på: rektangulär
cylindrisk
sfärisk
|
|
(Magnitude ± Angle)ÞcomplexValue (polär indata) Matar in ett komplext värde i (r±q) polär form. Angle tolkas enligt det inställda vinkelläget. |
I vinkelläget Radianer och i Rektangulärt komplext format:
Obs: För att få ett närmevärde, Handenhet: Tryck på / ·.
|
|
º tangent |
|
|
variable ' variable '' Skriver in en primsymbol i en differentialekvation. En enda primsymbol betecknar en differentialekvation av första ordningen, två primsymboler betecknar en ekvation av andra ordningen, och så vidare. |
|
|
Se “Tomma element” (här). |
|
|
|
|
|
/_ tangenter |
|
|
Expr_Unit Anger enheterna för ett Expr. Alla enhetsnamn måste börja med en understrykning. Du kan använda fördefinierade enheter eller skapa dina egna enheter. För en lista på fördefinierade enheter, öppna Katalogen och ta fram fliken Omvandling av enheter. Du kan välja enhetsnamn från Katalogen eller skriva in enhetsnamnen direkt. |
Obs: Du finner konverteringssymbolen 4 i Katalogen. Klicka på |
|
Variable_ När Variable inte har något värde behandlas den som om den representerar ett komplext tal. Som förinställning behandlas variabeln som reell utan _ . Om Variable har ett värde ignoreras _ och Variable behåller dess ursprungliga datatyp. Obs: Du kan lagra ett komplext tal i en variabel utan att använda _ . För bästa resultat i beräkningar såsom cSolve() och cZeros() rekommenderas dock _ . |
Förutsatt att z är odefinierad:
|
|
/k tangenter |
|||||||
|
Expr_Unit1 4 _Unit2ÞExpr_Unit2 Omvandlar ett uttryck från en enhet till en annan. Understrykningstecknet _ betecknar enheterna. Enheterna måste tillhöra samma kategori, till exempel, Längd eller Area. För en lista på fördefinierade enheter, öppna Katalogen och ta fram fliken Omvandling av enheter:
Du kan också skriva in enhetsnamnen manuellt. För att skriva “_” när du skriver enhetsnamn på handenheten, tryck på /_. Obs: För att konvertera temperaturenheter, använd tmpCnv() och @tmpCnv(). Konverteringsoperatorn 4 hanterar inte temperaturenheter. |
|
|
Katalog > |
|
|
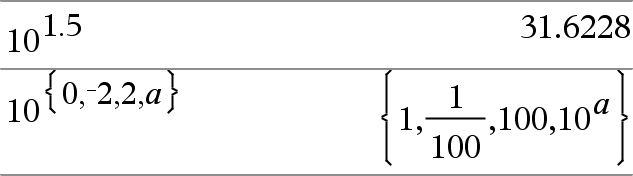
10^ (Expr1)Þuttryck 10^ (List1)Þlista Ger 10 upphöjd till argumentets potens. Ger, för en lista, 10 upphöjd till potensen för elementen i List1. |
|
|
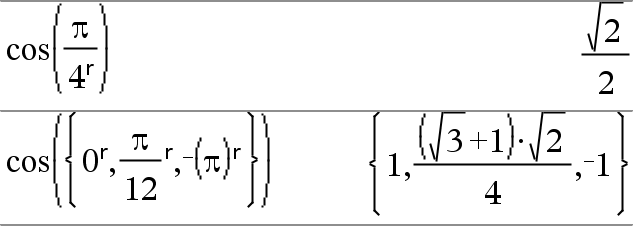
10^(squareMatrix1)ÞkvadratMatris Ger 10 upphöjd till potensen för squareMatrix1. Detta är inte detsamma som att beräkna 10 upphöjd till potensen för varje element. Se cos() för information om beräkningsmetoden. squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform. |
|
|
Katalog > |
|
|
List1 ^/Þlista Ger argumentets inverterade värde. Ger, för en lista, de inverterade värdena på elementen i List1. |
|
|
squareMatrix1 ^/ÞkvadratMatris Ger inversen av squareMatrix1. squareMatrix1 måste vara en icke singulär kvadratisk matris. |
|
|
/k tangenter |
||||||||||
|
Uttr | BoolesktUttr1 [ Uttr | BoolesktUttr1 [ (“|”)-symbolen begränsning fungerar som en binär operator. Operanden till vänster om | är ett uttryck. Operanden till höger om | specificerar ett eller flera relationer som är avsedda att påverka förenklingen av uttrycket. Flera relationer efter | måste förbindas med ett logiskt “ Operatorn begränsning ger tre bastyper av funktionalitet:
|
|
|||||||||
|
Substitutioner är i form av en likhet såsom x=3 eller y=sin(x). För bästa effektivitet bör den vänstra sidan vara en enkel variabel. Uttr | Variabel = värde ersätter värde vid varje förekomst av Variabel i Uttr. |
|
|||||||||
|
Intervallbegränsningar tar formen av en eller flera olikheter som förbinds med logiska “ |
|
|||||||||
|
Uteslutningar använder jämförelseoperatorn “inte lika med” (/= eller ƒ) för att utesluta ett specifikt värde från övervägning. |
|
|
/htangent |
|
|
List & Var Matrix & Var Expr & Function(Param1,...) List & Function(Param1,...) Matrix & Function(Param1,...) Om variabeln Var inte finns så skapas den och initialiseras till Expr, List eller Matrix. Om variabeln Var redan finns, och inte är låst eller skyddad, ersätts dess innehåll med Expr, List eller Matrix. Tips: Om du tänker göra symboliska beräkningar med odefinierade variabler, undvik att lagra någonting i enbokstaviga variabler som ofta används, till exempel, a, b, c, x, y, z, och så vidare. Obs: Du kan infoga denna operator med datorns tangentbord genom att skriva =: som kortkommando. Skriv exempelvis pi/4 =: minvar. |
|
|
/t tangenter |
|
|
Var := List Var := Matrix Function(Param1,...) := Expr Function(Param1,...) := List Function(Param1,...) := Matrix Om variabeln Var inte finns så skapas Var och initialiseras till Expr, List eller Matrix. Om Var redan finns, och inte är låst eller skyddad, ersätts dess innehåll med Expr, List eller Matrix.
|
|
|
/k tangenter |
|
|
© [text] © hanterar text som en kommentarsrad så att du kan kommentera funktioner och program som du skapar. © kan vara i början eller var som helst på raden. Allting till höger om ©, till slutet av raden, utgör kommentaren. Obs för att mata in exemplet: Se avsnittet Räknare i produkthandboken för instruktioner om hur du anger multiline-program och funktionsdefinitioner. |
|
|
0B tangenter, 0H tangenter |
|
|
0b binaryNumber 0h hexadecimalNumber Betecknar ett binärt respektive ett hexadecimalt tal. För att skriva in ett binärt eller hexadecimalt tal måste du använda prefixet 0b eller 0h oavsett det inställda basläget. Utan prefix behandlas ett tal som ett decimalt tal (bas 10). Resultaten visas enligt det inställda basläget. |
I decimalt basläge:
I binärt basläge:
I hexadecimalt basläge:
|









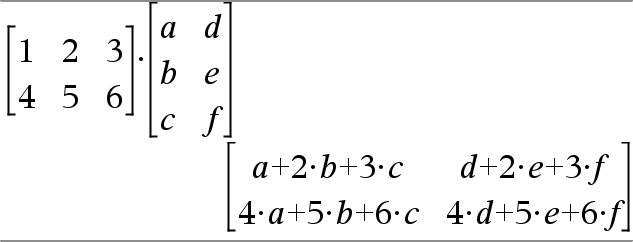












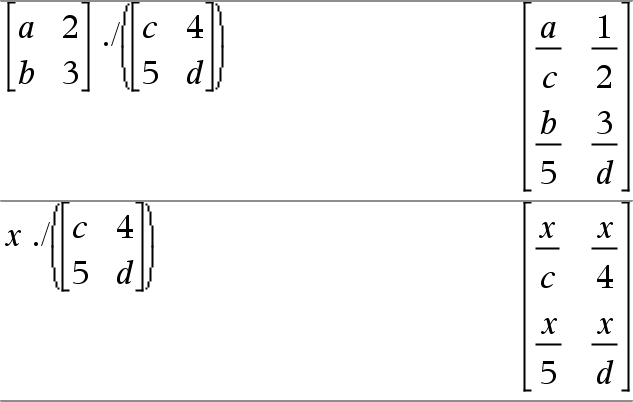

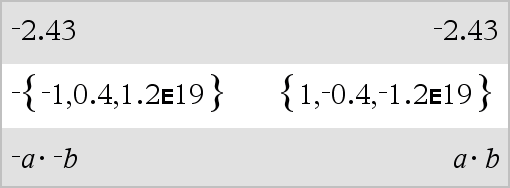
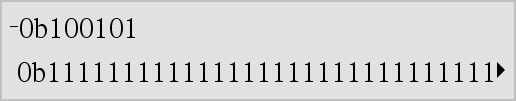
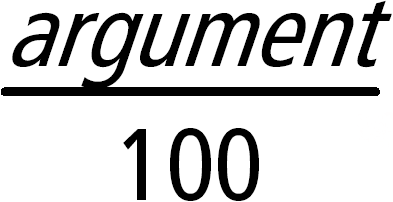
 .
.



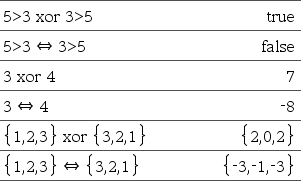



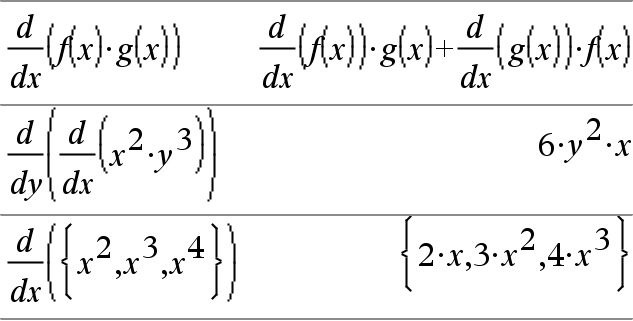


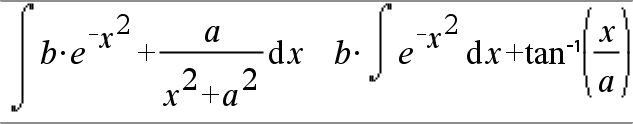

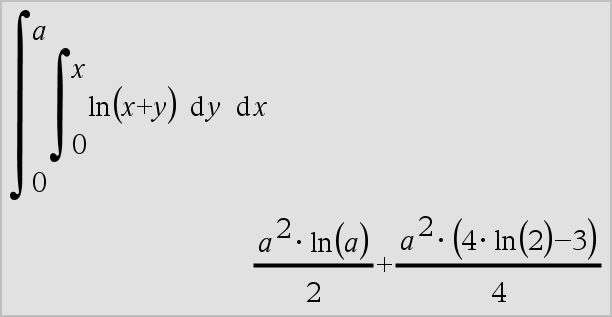

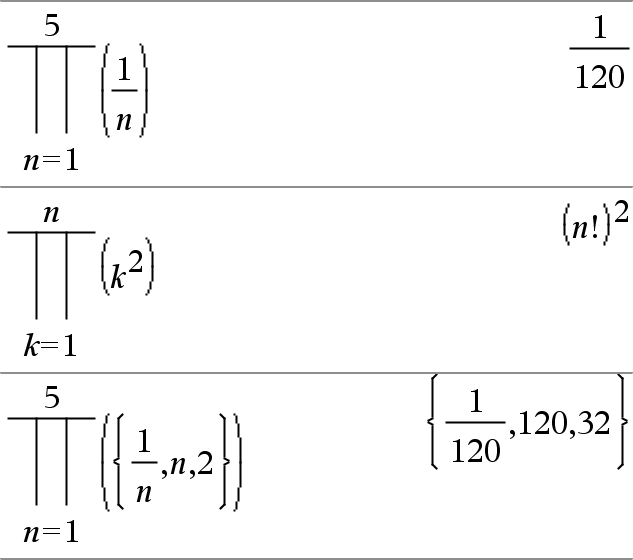

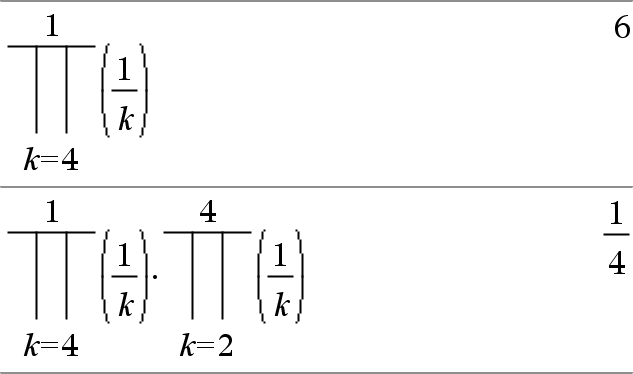
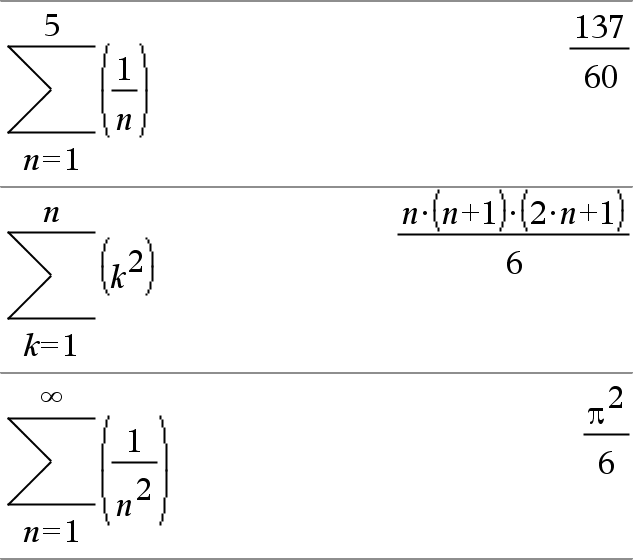

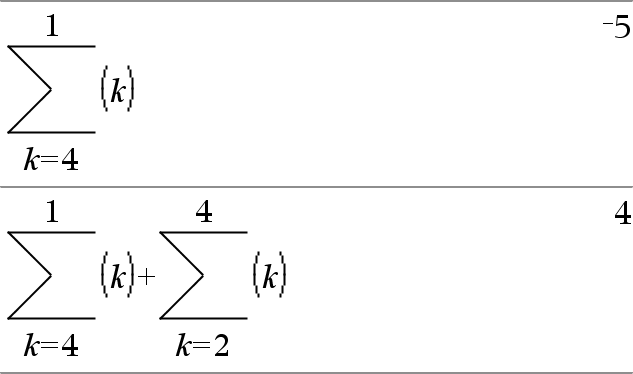
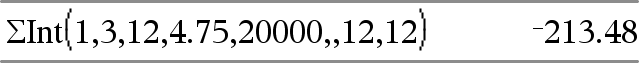
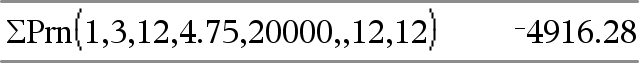






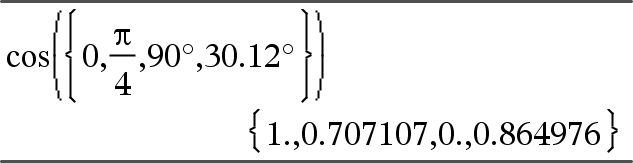

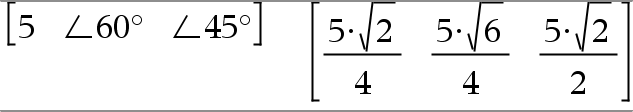
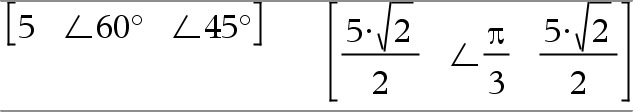

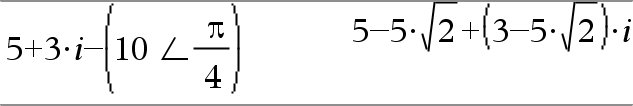
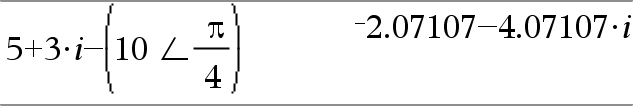
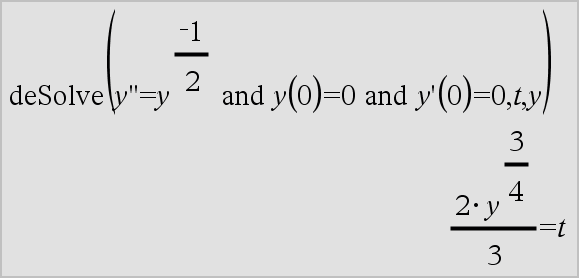

 och sedan på
och sedan på