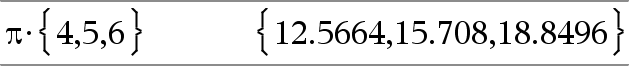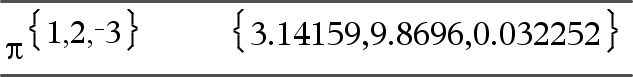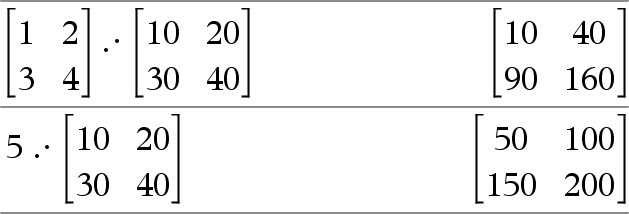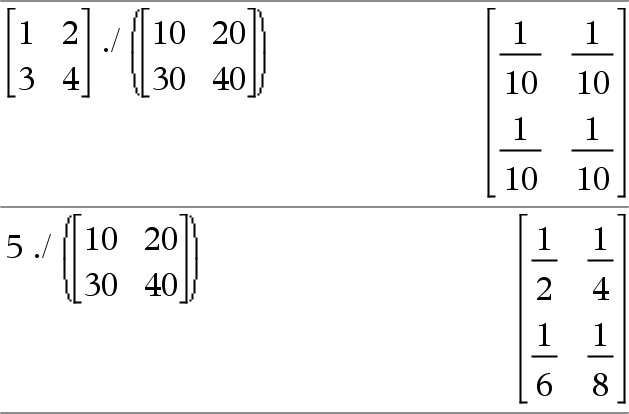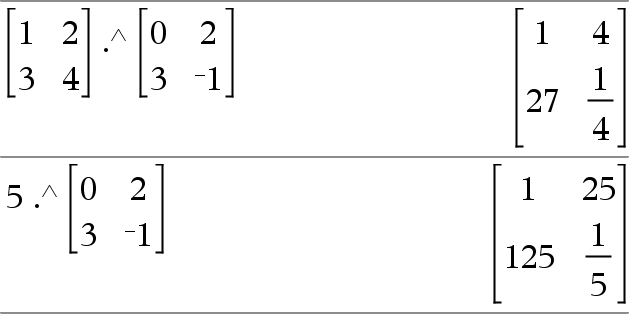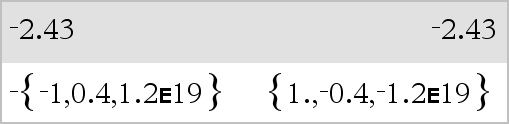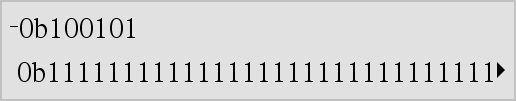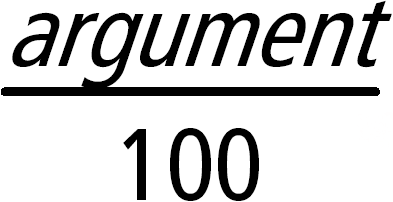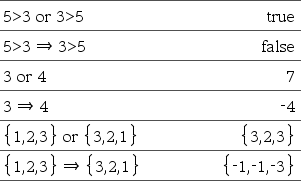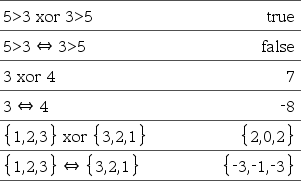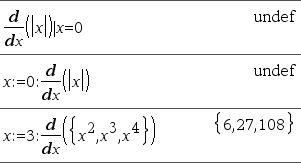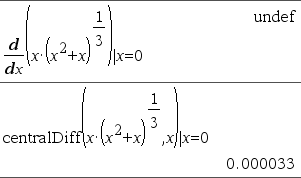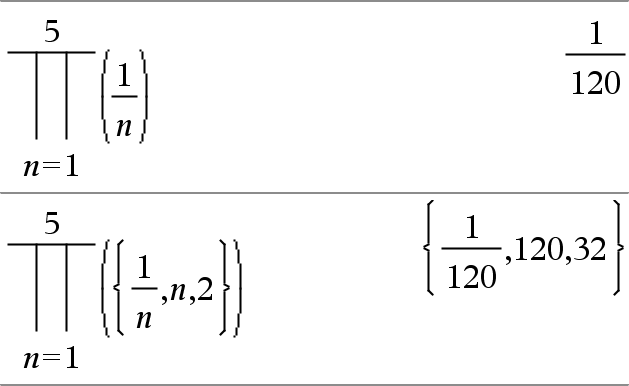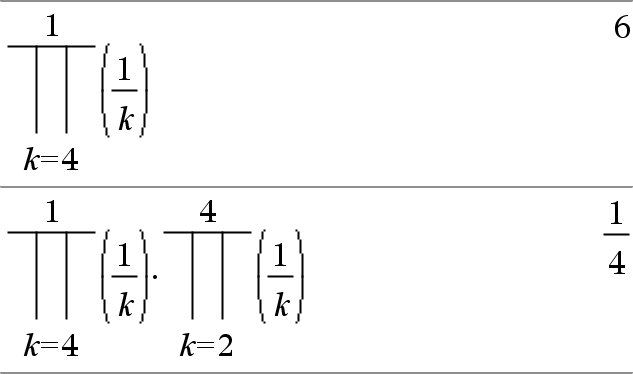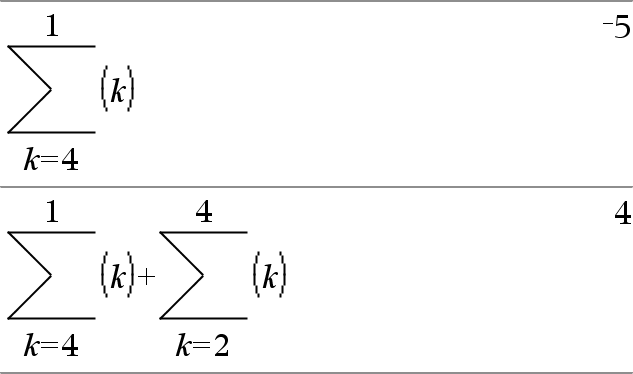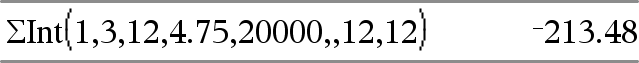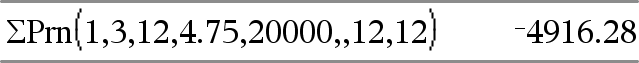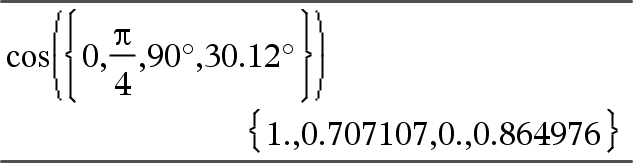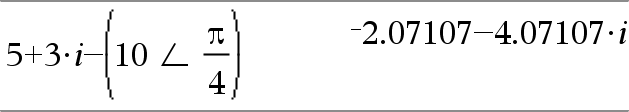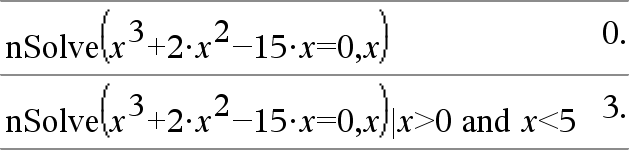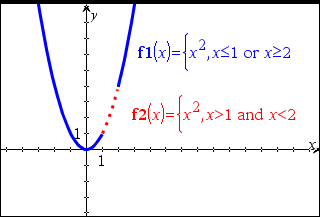|
+-toets |
|
|
Waarde1 + Waarde2Þwaarde Geeft de som van de twee argumenten. |
|
|
Lijst1 + Lijst2Þlijst Matrix1 + Matrix2Þmatrix Geeft een lijst (of matrix) met de som van de overeenkomstige elementen in Lijst1 en Lijst2 (of Matrix1 en Matrix2). De afmetingen van de argumenten moeten gelijk zijn. |
|
|
Lijst1 + WaardeÞlijst
|
|
|
Waarde + Matrix1Þmatrix Matrix1 + WaardeÞmatrix Geeft een matrix met Waarde opgeteld bij elk element op de diagonaal van Matrix1. Matrix1 moet vierkant zijn. Opmerking: gebruik .+ (punt plus) om een uitdrukking bij elk element op te tellen. |
|
|
--toets |
|
|
|
|
|
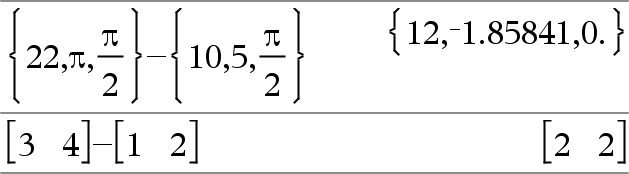
Lijst1 N Lijst2Þlijst Matrix1 N Matrix2Þmatrix Trekt elk element in Lijst2 (of Matrix2) af van het overeenkomstige element in Lijst1 (of Matrix1), en geeft de uitkomsten. De afmetingen van de argumenten moeten gelijk zijn. |
|
|
Lijst1 N WaardeÞlijst
|
|
|
Matrix1 N WaardeÞmatrix Waarde N Matrix1 geeft een matrix van Waarde keer de identiteitsmatrix min Matrix1. Matrix1 moet vierkant zijn. Matrix1 N Waarde geeft een matrix van Waarde keer de eenheidsmatrix afgetrokken van Matrix1. Matrix1 moet vierkant zijn. Opmerking: gebruik .N (punt min) om een uitdrukking van elk element af te trekken. |
|
|
r-toets |
|
|
Geeft het product van de twee argumenten. |
|
|
Lijst1 • Lijst2Þlijst Geeft een lijst met de producten van de overeenkomstige elementen in Lijst1 en Lijst2. De afmetingen van de lijsten moeten gelijk zijn. |
|
|
Matrix1•Matrix2Þmatrix Geeft het matrixproduct van Matrix1 en Matrix2. Het aantal kolommen in Matrix1 moet gelijk zijn aan het aantal rijen in Matrix2. |
|
|
Lijst1 • WaardeÞlijst
|
|
|
Matrix1 • WaardeÞmatrix Geeft een matrix met de producten van Waarde en elk element in Matrix1. Opmerking: gebruik .·(punt vermenigvuldigen) om een uitdrukking met elk element te vermenigvuldigen. |
|
|
p-toets |
|
|
Geeft het quotiënt van Waarde1 gedeeld door Waarde2. Opmerking: zie ook Breuk-template, hier. |
|
|
Lijst1 à Lijst2Þlijst Geeft een lijst met de quotiënten van Lijst1 gedeeld door Lijst2. De afmetingen van de lijsten moeten gelijk zijn. |
|
|
Waarde à Lijst1 Þ lijst Lijst1 à Waarde Þ lijst
|
|
|
Matrix1 à Waarde Þ matrix Geeft een matrix met de quotiënten van Matrix1àWaarde. Opmerking: gebruik . / (punt gedeeld door) om een uitdrukking door elk element te delen. |
|
|
l-toets |
|
|
Lijst1 ^ Lijst2 Þ lijst Geeft het eerste argument, verheven tot de macht van het twee argument. Opmerking: zie ook Exponent-template, hier. Geeft bij een lijst de elementen in Lijst1 verheven tot de macht van de overeenkomstige elementen in Lijst2. In het reële domein gebruiken gebroken machten die te vereenvoudigen zijn tot exponenten met oneven noemers de reële tak, versus de principaaltak voor de complexe modus. |
|
|
|
|
|
|
|
|
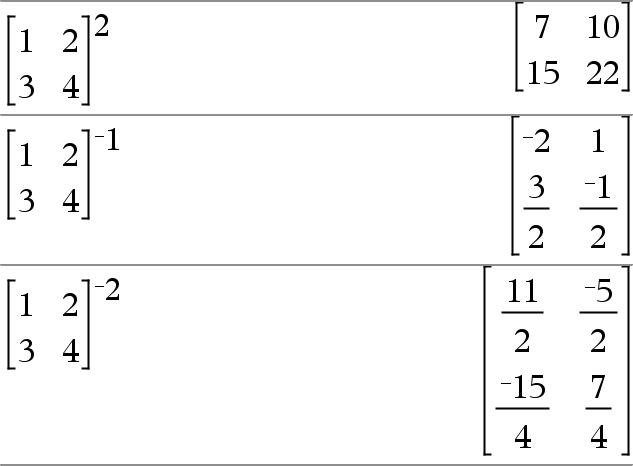
vierkanteMatrix1 ^ geheel getal Þ matrix Geeft vierkanteMatrix1 verheven tot de gehele macht. vierkanteMatrix1 moet een vierkante matrix zijn. Als geheel getal = L1 berekent dit commando de inverse matrix. Als geheel getal < L1 berekent dit commando de inverse matrix tot de passende positieve macht. |
|
|
q -toets |
|
|
Geeft het kwadraat van het argument. Lijst12 Þ lijst Geeft een lijst met de kwadraten van de elementen in Lijst1. vierkanteMatrix12 Þ matrix Geeft het matrixkwadraat van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van het kwadraat van elk element. Gebruik .^2 om het kwadraat van elk element te berekenen. |
|
|
^+-toetsen |
|
|
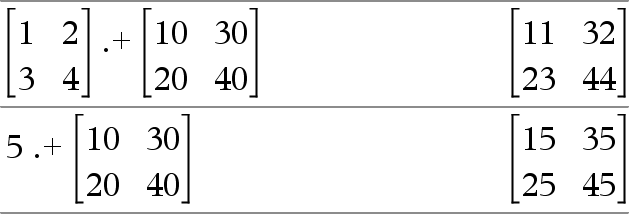
Matrix1 .+ Matrix2 Þ matrix
Matrix1 .+ Matrix2 geeft een matrix met de som van elk paar overeenkomstige elementen in Matrix1 en Matrix2.
|
|
|
^--toetsen |
|
|
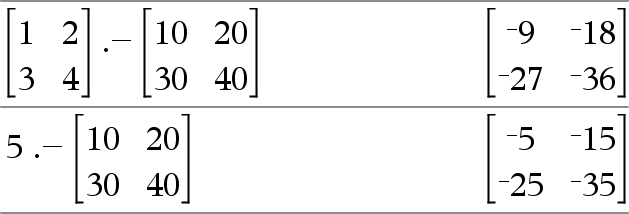
Matrix1 .N Matrix2 Þ matrix Matrix1 .NMatrix2 geeft een matrix met het verschil tussen elk paar overeenkomstige elementen in Matrix1 en Matrix2.
|
|
|
^r-toetsen |
|
|
Matrix1 .· Matrix2 Þ matrix
Matrix1 .· Matrix2 geeft een matrix met het product van elk paar overeenkomstige elementen in Matrix1 en Matrix2.
|
|
|
^p-toetsen |
|
|
Matrix1 . / Matrix2 Þ matrix
Matrix1 . / Matrix2 geeft een matrix met het quotiënt van elk paar overeenkomstige elementen in Matrix1 en Matrix2.
|
|
|
^l-toetsen |
|
|
Matrix1 .^ Matrix2 Þ matrix Matrix1 .^ Matrix2 geeft een matrix waarbij elk element in Matrix2 de exponent voor het overeenkomstige element in Matrix1 is.
|
|
|
v -toets |
|
|
LLijst1 Þ lijst LMatrix1 Þ matrix Geeft het tegengestelde van het argument. Geeft bij een lijst of matrix het tegengestelde van elk element. Als het argument een binair of hexadecimaal geheel getal is, geeft de negatie het twee-complement. |
In de Bin-grondtalmodus: Belangrijk: nul, niet de letter O.
Om het hele resultaat te zien drukt u op 5 en gebruikt u vervolgens 7 en 8 om de cursor te verplaatsen. |
|
/k-toetsen |
|
|
Lijst1 % Þ lijst Matrix1 % Þ matrix Geeft Geeft bij een lijst of matrix een lijst of matrix met elk element gedeeld door 100. |
|
|
= -toets |
|
|
Uitdr1 = Uitdr2ÞBooleaanse uitdrukking Lijst1 = Lijst2Þ Booleaanse lijst Matrix1 = Matrix2Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 gelijk is aan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 niet gelijk is aan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
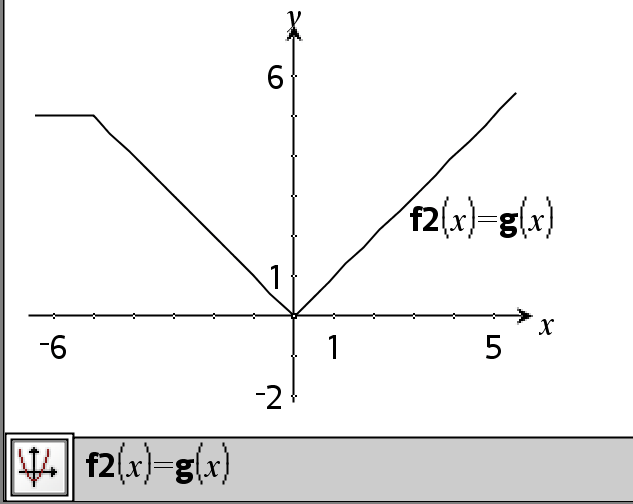
Voorbeeldfunctie waarin wiskundige test-symbolen worden gebruikt: =, ƒ, <, {, >, |
Resultaat van het tekenen van de grafiek g(x)
|
|
/=-toetsen |
|
|
Uitdr1 ƒ Uitdr2 Þ Booleaanse uitdrukking Lijst1 ƒ Lijst2 Þ Booleaanse lijst Matrix1 ƒ Matrix2 Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 niet gelijk is aan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 gelijk is aan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door /= in te typen |
Zie het voorbeeld voor “=” (is gelijk). |
|
/= toetsen |
|
|
Uitdr1 < Uitdr2 Þ Booleaanse uitdrukking Lijst1 < Lijst2 Þ Booleaanse lijst Matrix1 < Matrix2 Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 kleiner is dan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 groter dan of gelijk is aan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. |
Zie het voorbeeld voor “=” (is gelijk). |
|
/=-toetsen |
|
|
Uitdr1 { Uitdr2 Þ Booleaanse uitdrukking Lijst1 { Lijst2 Þ Booleaanse lijst Matrix1 { Matrix2 Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 kleiner dan of gelijk is aan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 groter is dan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door <= in te typen |
Zie het voorbeeld voor “=” (is gelijk). |
|
/=-toetsen |
|
|
Uitdr1 > Uitdr2 Þ Booleaanse uitdrukking Lijst1 > Lijst2 Þ Booleaanse lijst Matrix1 > Matrix2 Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 groter is dan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 kleiner dan of gelijk is aan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. |
Zie het voorbeeld voor “=” (is gelijk). |
|
/=-toetsen |
|
|
Uitdr1 | Uitdr2 Þ Booleaanse uitdrukking Lijst1 | Lijst2 Þ Booleaanse lijst Matrix1 | Matrix2 Þ Booleaanse matrix Geeft waar als vastgesteld is dat Uitdr1 groter dan of gelijk is aan Uitdr2. Geeft onwaar als vastgesteld is dat Uitdr1 kleiner is dan Uitdr2. Elke andere invoer geeft een vereenvoudigde vorm van de vergelijking. Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door >= in te typen |
Zie het voorbeeld voor “=” (is gelijk). |
|
/= toetsen |
|
|
BooleaanseUitdr1 Þ BooleaanseUitdr2 levertBooleaanse uitdrukking BooleaanseLijst1 ÞBooleaanseLijst2 levert Booleaanse lijst BooleaanseMatrix1 Þ BooleaanseMatrix2 levert Booleaanse matrix Geheel getal1 Þ Geheel getal2 levert Geheel getal
Werkt de uitdrukking Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoegen door => in te typen |
|
|
/= toetsen |
|
|
BooleaanseUitdr1 Û BooleaanseUitdr2 levert Booleaanse uitdrukking BooleaanseLijst1 ÛBooleaanseLijst2 levert Booleaanse lijst BooleaanseMatrix1 Û BooleaanseMatrix2 levert Booleaanse matrix Geheel getal1 Û Geheel getal2 levert Geheel getal
Geeft de ontkenning (negatie) van een Bij lijsten en matrices vergelijkt dit commando element voor element. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoegen door <=> in te typen |
|
|
º-toets |
|
|
Lijst1! Þ lijst Matrix1! Þ matrix Geeft de faculteit van het argument. Geeft bij een lijst of een matrix een lijst of een matrix met de faculteiten van de elementen. |
|
|
/k-toetsen |
|
|
String1 & String2 Þ string Geeft een tekststring die bestaat uit String2 toegevoegd aan String1. |
|
|
Catalogus > |
|
|
d(Uitdr1, Var[,Orde]) | Var=WaardeÞwaarde d(Uitdr1, Var[,Orde])Þwaarde d(Lijst1, Var[,Orde])Þlijst d(Matrix1, Var[,Orde])Þmatrix U moet een numerieke waarde in variabele Var opslaan voordat u d() uitwerkt, behalve als u de eerste syntax gebruikt. Zie de voorbeelden.
Orde moet, indien opgenomen, =1 of 2 zijn. De standaardwaarde is 1. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door
|
|
|
Zie het voorbeeld rechts. De eerste afgeleide van x·(x^2+x)^(1/3) voor x=0 is gelijk aan 0. Omdat de eerste afgeleide van de subuitdrukking (x^2+x)^(1/3) echter onbepaald is voor x=0, en deze waarde gebruikt wordt om de afgeleide van de gehele uitdrukking te berekenen, geeft d() de uitkomst als onbepaald weer en toont een waarschuwingsbericht.
|
|
|
Catalogus > |
|
|
‰(Uitdr1, Var, Onder, Boven) Þ waarde Geeft de integraal van Uitdr1 ten opzichte van de variabele Var van Onder tot Boven. Kan worden gebruikt om de bepaalde integraal numeriek te berekenen, met dezelfde methode als nInt(). Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door integral(...) in te typen. Opmerking: zie ook nInt(), hier en Bepaalde integraal-template, hier. |
|
|
/q-toetsen |
|
|
‡ (Lijst1)Þlijst Geeft de wortel van het argument. Geeft bij een lijst de wortel van alle elementen in Lijst1. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door sqrt(...) in te typen. Opmerking: zie ook Wortel-template, hier. |
|
|
Catalogus > |
|
|
P(Uitdr1, Var, Laag, Hoog)Þuitdrukking Werkt Uitdr1 uit voor elke waarde van Var van Laag tot Hoog, en geeft het product van de resultaten. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door prodSeq(...) in te typen. Werkt Uitdr1 uit voor elke waarde van Var van Laag tot Hoog, en geeft het product van de resultaten. Opmerking: zie ook Product-template (P), hier. |
|
|
P(Uitdr1, Var, Laag, LaagN1)Þ1 P(Uitdr1, Var, Laag, Hoog) Þ1/P(Uitdr1, Var, Hoog+1, LaagN1) als Hoog < LaagN1 De gebruikte productformules zijn afkomstig uit de volgende bron: Ronald L. Graham, Donald E. Knuth en Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalogus > |
|
|
G(Uitdr1, Var, Laag, Hoog)Þuitdrukking Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door sumSeq(...) in te typen. Werkt Uitdr1 uit voor elke waarde van Var van Laag naar Hoog, en geeft de som van de resultaten. Opmerking: Zie ook Som-template, hier. |
|
|
G(Uitdr1, Var, Laag, LaagN1)Þ0 G(Uitdr1, Var, Laag, Hoog) ÞLG(Uitdr1, Var, Hoog+1, LaagN1) als Hoog < LaagN1
De gebruikte somformules zijn afkomstig uit de volgende bron: Ronald L. Graham, Donald E. Knuth en Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalogus > |
||||||||||
|
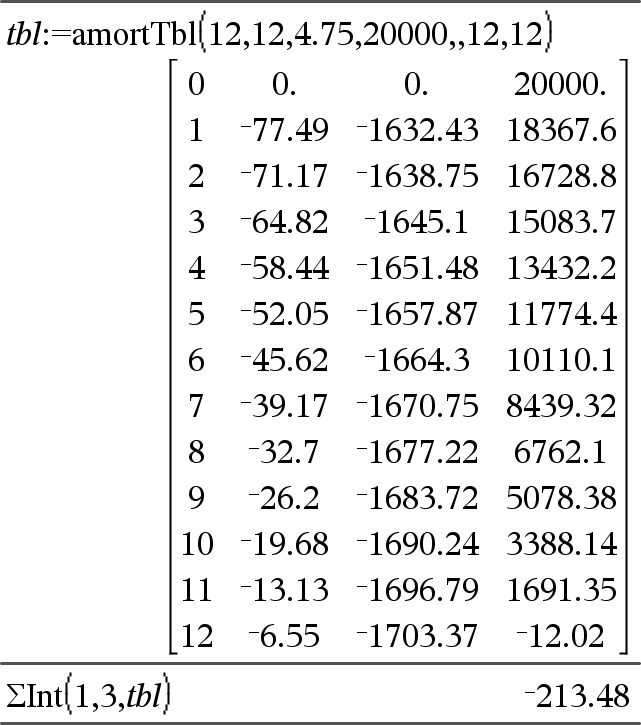
GInt(NPmt1, NPmt2, N, I, PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [afgerondeWaarde])Þwaarde GInt(NPmt1,NPmt2,amortTable)Þwaarde Aflossingsfunctie die de som van de rente gedurende een gespecificeerd aantal betalingen berekent. NPmt1 en NPmt2 definiëren de begin- en eindgrenzen van het betalingsbereik. N, I, PV, Pmt, FV, PpY, CpY en PmtAt worden beschreven in de tabel met TVM-argumenten, hier.
afgerondeWaarde specificeert het aantal decimalen voor afronding. Standaardwaarde=2. GInt(NPmt1,NPmt2,amortTable) berekent de som van de rente op basis van de aflossingstabel amortTable. Het argument amortTable moet een matrix zijn met de vorm die beschreven wordt onder amortTbl(), hier. Opmerking: zie ook GPrn(), hieronder, en Bal(), hier. |
|
|
Catalogus > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [afgerondeWaarde])Þwaarde GPrn(NPmt1,NPmt2,amortTable)Þwaarde Aflossingsfunctie die de som van de hoofdsom gedurende een gespecificeerd aantal betalingen berekent. NPmt1 en NPmt2 definiëren de begin- en eindgrenzen van het betalingsbereik. N, I, PV, Pmt, FV, PpY, CpY en PmtAt worden beschreven in de tabel met TVM-argumenten, hier.
afgerondeWaarde specificeert het aantal decimalen voor afronding. Standaardwaarde=2. GPrn(NPmt1,NPmt2,amortTable) berekent de som van de betaalde hoofdsom op basis van de aflossingstabel amortTable. Het argument amortTable moet een matrix zijn met de vorm die beschreven wordt onder amortTbl(), hier. Opmerking: zie ook GInt(), hierboven, en Bal(), hier. |
|
|
/k-toetsen |
|
|
# varNaamString Verwijst naar de variabele met de naam varNaamString. Hiermee kunt u strings gebruiken om variabelenamen binnen een functie te creëren. |
Creëert of verwijst naar de variabele xyz.
Geeft de waarde van de variabele (r) waarvan de naam is opgeslagen in variabele s1. |
|
i-toets |
|
|
mantisseEexponent Voert een getal in wetenschappelijke notatie in. Het getal wordt geïnterpreteerd als mantisse × 10exponent. Tip: als u een macht van 10 wilt invoeren zonder een resultaat met decimalen te veroorzaken, gebruik dan 10^geheel getal. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @E in te typen. typ bijvoorbeeld 2.3@E4 om 2.3E4 in te voeren. |
|
|
1-toets |
|
|
Lijst1gÞlijst Matrix1gÞmatrix Deze functie geeft u een manier om een hoek in decimale graden te specificeren terwijl u in de modus Graden of Radialen bent. In de hoekmodus Radialen: vermenigvuldigt Uitdr1 met p/200. In de hoekmodus Graden: vermenigvuldigt Uitdr1 met g/100. In de modus Decimale graden: geeft Uitdr1 ongewijzigd. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @g in te voeren. |
In de modus Graden, Decimale graden of Radialen:
|
|
1-toets |
|
|
Lijst1RÞlijst Matrix1RÞmatrix Deze functie geeft u een manier om een hoek in radialen te specificeren terwijl u in de modus Graden of Decimale graden bent. In de hoekmodus Graden: vermenigvuldigt het argument met 180/p. In de hoekmodus Radialen: geeft het argument ongewijzigd. In de modus Decimale graden: vermenigvuldigt het argument met 200/p. Tip: gebruik Rals u radialen wilt forceren in een functiedefinitie, ongeacht de modus die de voorkeur heeft wanneer de functie wordt gebruikt. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @r in te voeren. |
In de hoekmodus Graden, Decimale graden of Radialen:
|
|
1-toets |
|
|
Lijst1¡Þlijst Matrix1¡Þmatrix Deze functie geeft u een manier om een hoek in graden te specificeren terwijl u in de modus Decimale graden of Radialen bent. In de hoekmodus Radialen: vermenigvuldigt het argument met p/180. In de hoekmodus Graden: geeft het argument ongewijzigd. In de hoekmodus Decimale graden: vermenigvuldigt het argument met 10/9. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @d in te voeren. |
In de hoekmodus Graden, Decimale graden of Radialen:
In de hoekmodus Radialen:
|
|
/k-toetsen |
|||||||
|
dd¡mm'ss.ss''Þuitdrukking ddEen positief of negatief getal mmEen niet-negatief getal ss.ssEen niet-negatief getal Geeft dd+(mm/60)+(ss.ss/3600). Met deze grondtal‑60-invoeropmaak kunt u:
Opmerking: laat ss.ss volgen door twee apostroffen (''), niet door een dubbel aanhalingsteken ("). |
In de hoekmodus Graden:
|
|
/k-toetsen |
|
|
[Straal,±q_Hoek]Þvector (polaire invoer) [Straal,±q_Hoek,Z_Coördinaat]Þvector (cilindrische invoer) [Straal,±q_Hoek,±q_Hoek]Þvector (bolvormige invoer) Geeft coördinaten als een vector op basis van de modusinstelling voor vectoropmaak: rechthoekig, cilindrisch of bolvormig. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door @< in te voeren. |
In de modus Radialen en met vectoropmaak ingesteld op: rechthoekig
cilindrisch
bolvormig
|
|
(Grootte ± Hoek)ÞcomplexeWaarde (polaire invoer) Voert een complexe waarde in (r±q) polaire vorm in. De Hoek wordt geïnterpreteerd volgens de huidige instelling van de hoekmodus. |
In de hoekmodus Radialen en rechthoekige complexe opmaak:
|
|
Zie “Lege elementen” hier. |
|
|
|
|
|
Catalogus > |
|
|
10^ (Waarde1)Þwaarde 10^ (Lijst1)Þlijst Geeft 10 tot de macht van het argument. Geeft bij een lijst 10 tot de macht van de elementen in Lijst1. |
|
|
10^(vierkanteMatrix1)ÞvierkanteMatrix Geeft 10 tot de macht van vierkanteMatrix1. Dit is niet hetzelfde als het berekenen van 10 tot de macht van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
|
|
Catalogus > |
|
|
Lijst1 ^/Þlijst Geeft de omgekeerde van het argument. Geeft bij een lijst de omgekeerden van de elementen in Lijst1. |
|
|
vierkanteMatrix1 ^/ÞvierkanteMatrix Geeft de inverse van vierkanteMatrix1. vierkanteMatrix1 moet een niet-singuliere vierkante matrix zijn. |
|
|
/k-toetsen |
||||||||||
|
Uitdr | BooleaanseUitdr1 [ Uitdr | BooleaanseUitdr1 [ Het beperkingssymbool (“|”) dient als een binaire operator. De operand aan de linkerkant van | is een uitdrukking. De operand aan de rechterkant van | specificeert één of meer relaties die bedoeld zijn om de vereenvoudiging van de uitdrukking te beïnvloeden. Meerdere relaties na | moeten gekoppeld worden door logische “ De beperkings-operator biedt drie basistypen functionaliteit:
|
|
|||||||||
|
Substituties zijn in de vorm van een gelijkheid, zoals x=3 of y=sin(x). Om het meest effectief te zijn moet de linkerkant een enkelvoudige variabele zijn. Uitdr | Variabele = waarde substitueert waarde elke keer dat Variabele voorkomt in Uitdr. |
|
|||||||||
|
Intervalbeperkingen kunnen de vorm aannemen van één of meer ongelijkheden die gekoppeld worden door logische “and” of “or”-operatoren. Intervalbeperkingen maken ook vereenvoudigingen mogelijk, die anders ongeldig of niet te berekenen zouden kunnen zijn. |
|
|||||||||
|
Uitsluitingen gebruiken de relationele operator “is niet gelijk aan” (/= of ƒ) om een specifieke waarde buiten beschouwing te laten. |
|
/h-toets |
|
|
Lijst & Var Matrix & Var Uitdr & Functie(Param1,...) Lijst & Functie(Param1,...) Matrix & Functie(Param1,...) Als de variabele Var niet bestaat, dan wordt deze gecreëerd en geïnitialiseerd naar Waarde, Lijst of Matrix. Als de variabele Var reeds bestaat en niet vergrendeld of beveiligd is, dan wordt de inhoud ervan vervangen door Waarde, Lijst of Matrix. Opmerking: u kunt deze operator vanaf het toetsenbord van de computer invoeren door =: als sneltoets in te voeren. Typ bijvoorbeeld pi/4 =: mijnvar. |
|
|
/t -toetsen |
|
|
Var := Lijst Var := Matrix Functie(Param1,...) := Uitdr Functie(Param1,...) := Lijst Functie(Param1,...) := Matrix Als variabele Var niet bestaat, dan wordt Var gecreëerd en geïnitialiseerd naar Waarde, Lijst of Matrix. Als Var reeds bestaat en niet vergrendeld of beveiligd is, dan wordt de inhoud ervan vervangen door Waarde, Lijst of Matrix. |
|
|
/k-toetsen |
|
|
© [tekst] © verwerkt tekst als een commentaarregel, waardoor u door u gecreëerde functies en programma's kunt annoteren. © kan aan het begin of op een willekeurige plaats in de regel staan. Alles rechts van ©, tot aan het eind van de regel, is het commentaar. Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
|
|
0B-toetsen, 0H-toetsen |
|
|
0b binairGetal 0h hexadecimaalGetal Duidt respectievelijk een binair of hexadecimaal getal aan. Om een binair of hexadecimaal getal in te voeren moet u het 0b- of 0h-prefix invoeren, ongeacht de instelling van de grondtal-modus. Zonder prefix wordt een getal behandeld als decimaal (grondtal 10). Resultaten worden weergegeven volgens de grondtal-modus. |
In de Dec-grondtalmodus:
In de Bin-grondtalmodus:
In de Hex-grondtalmodus:
|