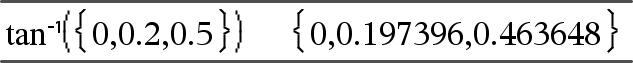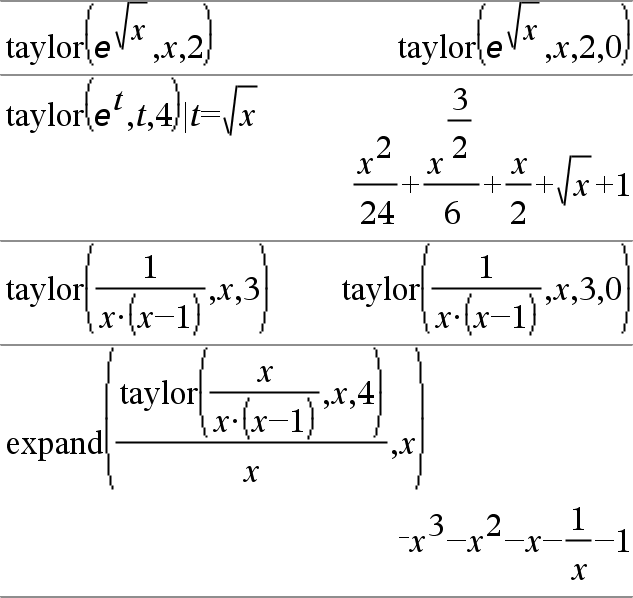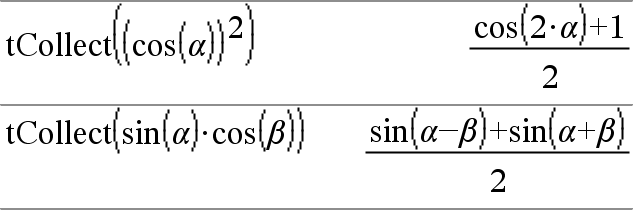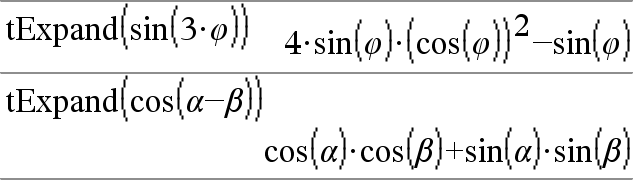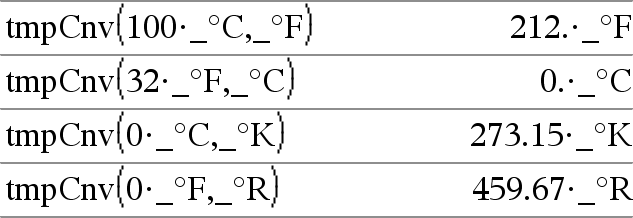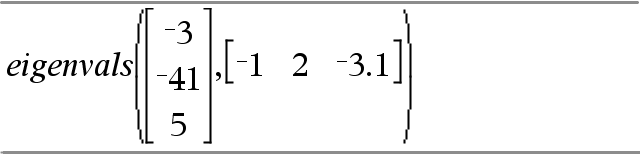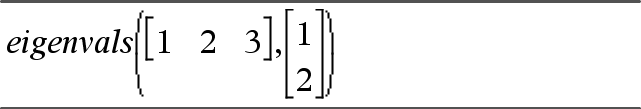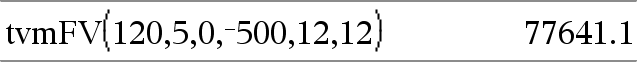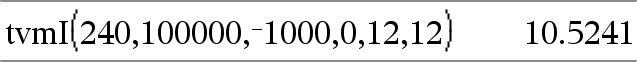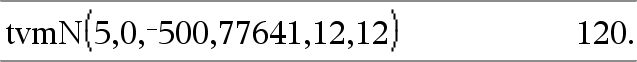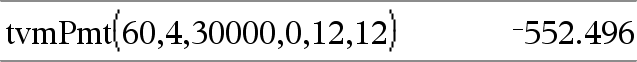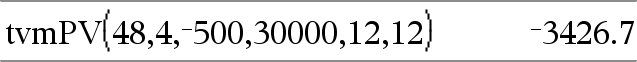|
Katalog > |
|
|
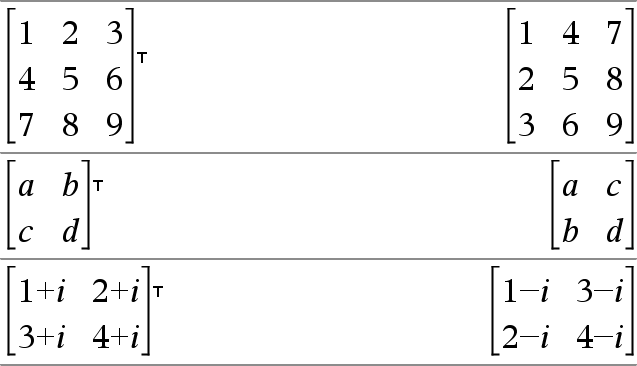
Matrix1TÞmatrix Gibt die komplex konjugierte, transponierte Matrix von Matrix1 zurück. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @t eintippen. |
|
|
µ Taste |
|
|
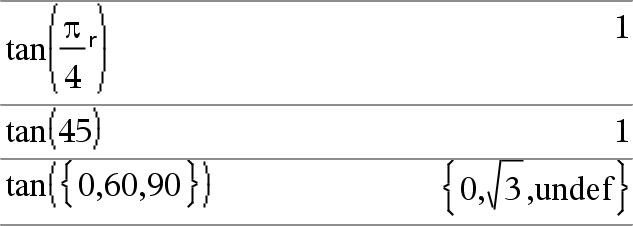
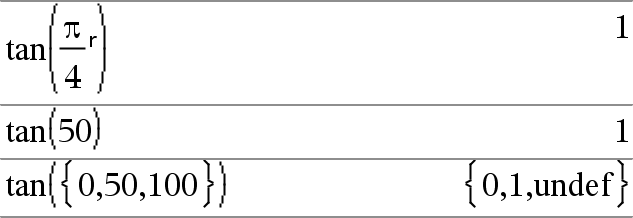
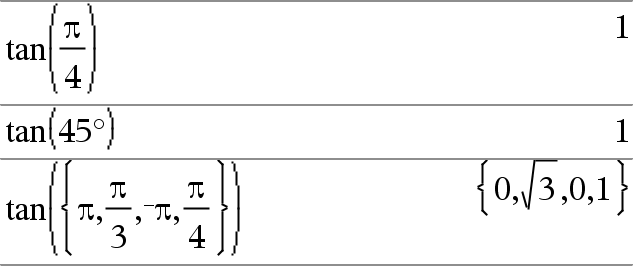
tan(Ausdr1)ÞAusdruck tan(Liste1)ÞListe
tan(Liste1) gibt in Form einer Liste für jedes Element in Liste1 den Tangens zurück. Hinweis: Das Argument wird entsprechend dem aktuellen Winkelmodus als Winkel in Grad, Neugrad oder Bogenmaß interpretiert. Sie können ¡, G oder R benutzen, um die Winkelmoduseinstellung temporär zu ändern. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
tan(Quadratmatrix1)ÞQuadratmatrix Gibt den Matrix-Tangens von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Tangens jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Bogenmaß-Modus:
|
|
µ Taste |
|
|
tan/(Ausdr1)ÞAusdruck tan/(Liste1)ÞListe
tan/(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den inversen Tangens zurück. Hinweis: Das Ergebnis wird gemäß der aktuellen Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arctan(...) eintippen. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
tan/(Quadratmatrix1)ÞQuadratmatrix Gibt den inversen Matrix-Tangens von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Tangens jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
tangentLine(Ausdr1,Var,Punkt)ÞAusdruck tangentLine(Ausdr1,Var=Punkt)ÞAusdruck Gibt die Tangente zu der durch Ausdr1 dargestellten Kurve an dem in Var=Punkt angegebenen Punkt zurück. Stellen Sie sicher, dass die unabhängige Variable nicht definiert ist. Wenn zum Beispiel f1(x):=5 und x:=3 ist, gibt tangentLine(f1(x),x,2) “false” zurück. |
|
|
Katalog > |
|
|
tanh(Ausdr1)ÞAusdruck tanh(Liste1)ÞListe
tanh(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den Tangens hyperbolicus zurück. |
|
|
tanh(Quadratmatrix1)ÞQuadratmatrix Gibt den Matrix-Tangens hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Tangens hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
tanh/(Ausdr1)ÞAusdruck tanh/(Liste1)ÞListe
tanh/(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den inversen Tangens hyperbolicus zurück. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arctanh(...) eintippen. |
Im Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
tanh/(Quadratmatrix1)ÞQuadratmatrix Gibt den inversen Matrix-Tangens hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Tangens hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
Katalog > |
|
|
taylor(Ausdr1, Var, Ordnung[, Punkt])ÞAusdruck Gibt das angeforderte Taylor-Polynom zurück. Das Polynom enthält alle ganzzahligen Potenzen von (Var minus Punkt) mit nicht verschwindenden Koeffizienten von Null bis Ordnung. taylor() gibt sich selbst zurück, wenn es keine endliche Potenzreihe dieser Ordnung gibt oder negative oder Bruchexponenten erforderlich wären. Benutzen Sie Substitution und/oder die temporäre Multiplikation mit einer Potenz (Var minus Punkt), um allgemeinere Potenzreihen zu ermitteln. Punkt ist vorgegeben als Null und ist der Entwicklungspunkt. |
|
|
Katalog > |
|
|
tCdf(UntGrenze,ObGrenze,FreiGrad)ÞZahl, wenn UntGrenze und ObGrenze Zahlen sind, Liste, wenn UntGrenze und ObGrenze Listen sind Berechnet für eine Student-t-Verteilung mit vorgegebenen Freiheitsgraden FreiGrad die Intervallwahrscheinlichkeit zwischen UntGrenze und ObGrenze. Für P(X { obereGrenze) setzen Sie untereGrenze = .ˆ. |
|
|
Katalog > |
|
|
tCollect(Ausdr1)ÞAusdruck Gibt einen Ausdruck zurück, in dem Produkte und ganzzahlige Potenzen von Sinus und Cosinus in eine lineare Kombination von Sinus und Cosinus von Winkelvielfachen, Winkelsummen und Winkeldifferenzen umgewandelt sind. Diese Transformation wandelt trigonometrische Polynome in eine lineare Kombination um. In manchen Fällen führt tCollect() zum Erfolg, wo die vorgegebene trigonometrische Vereinfachung nicht zum Erfolg führt. tCollect() bewirkt in beinahe allen Fällen eine Umkehrung von Transformationen, die mit tExpand() vorgenommen wurden. Manchmal lässt sich ein Ausdruck vereinfachen, wenn man in getrenntenSchritten tExpand() auf ein Ergebnis von tCollect() anwendet (oder umgekehrt). |
|
|
Katalog > |
|
|
tExpand(Ausdr1)ÞAusdruck Gibt einen Ausdruck zurück, in dem Sinus und Cosinus von ganzzahligen Winkelvielfachen, Winkelsummen und Winkeldifferenzen entwickelt sind. Aufgrund der Identität (sin(x))2+(cos(x))2=1 sind viele äquivalente Ergebnisse möglich. Ein Ergebnis kann sich daher von einem in anderen Publikationen angegebenen unterscheiden. In manchen Fällen führt tExpand() zum Erfolg, wo die vorgegebene trigonometrische Vereinfachung nicht zum Erfolg führt. tExpand() bewirkt in beinahe allen Fällen eine Umkehrung von Transformationen, die mit tCollect() vorgenommen wurden. Manchmal lässt sich ein Ausdruck vereinfachen, wenn man in getrenntenSchritten tCollect() auf ein Ergebnis von tExpand() anwendet (oder umgekehrt). Hinweis: Die Skalierung von p/180 im Winkelmodus “Grad” behindert die Erkennung entwickelbarer Formen durch tExpand(). Die besten Ergebnisse werden bei Benutzung von tExpand() im Bogenmaß-Modus erzielt. |
|
|
Katalog > |
|||||||
|
Programmierbefehl: Pausiert das Programm und zeigt die Zeichenkette EingabeString in einem Dialogfeld an. Wenn der Benutzer OK auswählt, wird die Programmausführung fortgesetzt. Bei dem optionalen Argument FlagAnz kann es sich um einen beliebigen Ausdruck handeln.
Wenn das Programm eine Eingabe vom Benutzer benötigt, verwenden Sie stattdessen Hinweis: Sie können diesen Befehl in benutzerdefinierten Programmen, aber nicht in Funktionen verwenden. |
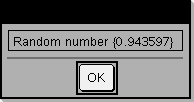
Definieren Sie ein Programm, das fünfmal anhält und jeweils eine Zufallszahl in einem Dialogfeld anzeigt. Schließen Sie in der Vorlage Prgm...EndPrgm jede Zeile mit @ ab anstatt mit ·. Auf der Computertastatur halten Sie Alt gedrückt und drücken die Eingabetaste.
Define text_demo()=Prgm For i,1,5 strinfo:=”Random number “ & string(rand(i)) Text strinfo EndFor EndPrgm
Starten Sie das Programm: text_demo()
Muster eines Dialogfelds:
|
|
Siehe If, hier. |
|
|
|
|
|
Katalog > |
|
|
tInterval Liste[,Häuf[,KNiv]] (Datenlisteneingabe) tInterval v,sx,n[,KNiv] (Zusammenfassende statistische Eingabe) Berechnet das Konfidenzintervall t. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (hier.) Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.CLower, stat.CUpper |
Konfidenzintervall für den unbekannten Populationsmittelwert |
|
stat.x |
Stichprobenmittelwert der Datenfolge aus der zufälligen Normalverteilung |
|
stat.ME |
Fehlertoleranz |
|
stat.df |
Freiheitsgrade |
|
stat.sx |
Stichproben-Standardabweichung |
|
stat.n |
Länge der Datenfolge mit Stichprobenmittelwert |
|
Katalog > |
|
|
tInterval_2Samp Liste1,Liste2[,Häufigkeit1[,Häufigkeit2[,KStufe[,Verteilt]]]] (Datenlisteneingabe) tInterval_2Samp v1,sx1,n1,v2,sx2,n2[,KStufe[,Verteilt]] (Zusammenfassende statistische Eingabe) Berechnet ein t-Konfidenzintervall für zwei Stichproben. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (hier.) Verteilt=1 verteilt Varianzen; Verteilt=0 verteilt keine Varianzen. Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.CLower, stat.CUpper |
Konfidenzintervall mit dem Konfidenzniveau der Verteilungswahrscheinlichkeit |
|
stat.x1-x2 |
Stichprobenmittelwerte der Datenfolgen aus der zufälligen Normalverteilung |
|
stat.ME |
Fehlertoleranz |
|
stat.df |
Freiheitsgrade |
|
stat.x1, stat.x2 |
Stichprobenmittelwerte der Datenfolgen aus der zufälligen Normalverteilung |
|
stat.sx1, stat.sx2 |
Stichproben-Standardabweichungen für Liste 1 und Liste 2 |
|
stat.n1, stat.n2 |
Anzahl der Stichproben in Datenfolgen |
|
stat.sp |
Die verteilte Standardabweichung. Wird berechnet, wenn Verteilt = JA. |
|
Katalog > |
|
|
tmpCnv(Ausdr_¡TempEinh, _¡TempEinh2) ÞAusdruck _¡TempEinh2 Konvertiert einen durch Ausdr definierten Temperaturwert von einer Einheit in eine andere. Folgende Temperatureinheiten sind gültig: _¡C Celsius _¡F Fahrenheit _¡K Kelvin _¡R Rankine Wählen Sie zur Eingabe von ¡ das Symbol aus der Sonderzeichenpalette des Katalogs aus. Zur Eingabe von _ drücken Sie /_. 100_¡C wird zum Beispiel in 212_¡F konvertiert. Zur Konvertierung eines Temperaturbereichs verwenden Sie hingegen @tmpCnv(). |
Hinweis: Sie können den Katalog verwenden, um Temperatureinheiten auszuwählen. |
|
Katalog > |
|
|
@tmpCnv(Ausdr_¡tempEinh, _¡tempEinh2) ÞAusdruck _¡tempEinh2 Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie deltaTmpCnv(...) eintippen. Konvertiert einen durch Ausdr definierten Temperaturbereich (Differenz zwischen zwei Temperaturwerten) von einer Einheit in eine andere. Folgende Temperatureinheiten sind gültig: _¡C Celsius _¡F Fahrenheit _¡K Kelvin _¡R Rankine Wählen Sie zur Eingabe von ¡ das Symbol aus der Sonderzeichenpalette oder geben Sie @d ein. Zur Eingabe von _ drücken Sie /_. 1_¡C und 1_¡K haben denselben Absolutwert, ebenso wie 1_¡F und 1_¡R. 1_¡C ist allerdings 9/5 so groß wie 1_¡F. Ein 100_¡C Bereich (von 0_¡C bis 100_¡C) ist beispielsweise einem 180_¡F Bereich äquivalent. Zur Konvertierung eines bestimmten Temperaturwerts verwenden Sie hingegen tmpCnv(). |
Wählen Sie zur Eingabe von @ das Symbol aus der Sonderzeichenpalette des Katalogs aus.
Hinweis: Sie können den Katalog verwenden, um Temperatureinheiten auszuwählen. |
|
Katalog > |
|
|
tPdf(XWert,FreiGrad)ÞZahl, wenn XWert eine Zahl ist, Liste, wenn XWert eine Liste ist Berechnet die Wahrscheinlichkeitsdichtefunktion (Pdf) einer Student-t-Verteilung an einem bestimmten x-Wert für die vorgegebenen FreiheitsgradeFreiGrad. |
|
|
Katalog > |
|
|
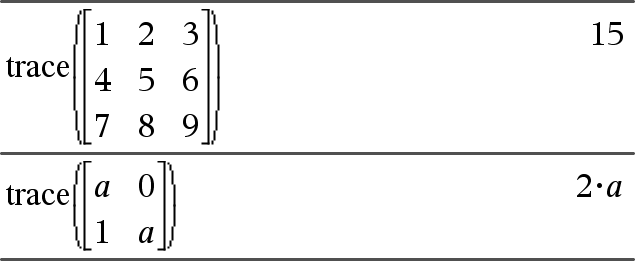
trace(Quadratmatrix)ÞAusdruck Gibt die Spur (Summe aller Elemente der Hauptdiagonalen) von Quadratmatrix zurück. |
|
|
Katalog > |
|
|
Try Führt Block1 aus, bis ein Fehler auftritt. Wenn in Block1 ein Fehler auftritt, wird die Programmausführung an Block2 übertragen. Die Systemvariable Fehlercode (errCode) enthält den Fehlercode, der es dem Programm ermöglicht, eine Fehlerwiederherstellung durchzuführen. Eine Liste der Fehlercodes finden Sie unter “Fehlercodes und -meldungen” (hier). Block1 und Block2 können einzelne Anweisungen oder Reihen von Anweisungen sein, die durch das Zeichen “:” voneinander getrennt sind. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
|
|
Um die Befehle Versuche (Try), LöFehler (ClrErr) und ÜbgebFeh (PassErr) im Betrieb zu sehen, geben Sie das rechts gezeigte Programm eigenvals() ein. Sie starten das Programm, indem Sie jeden der folgenden Ausdrücke eingeben.
|
Definiere eigenvals(a,b)=Prgm © Programm eigenvals(A,B) zeigt die Eigenwerte von A·B an Try Disp "A= ",a Disp "B= ",b Disp " " Disp "Eigenwerte von A·B sind:",eigVl(a*b) Else If errCode=230 Then Disp "Fehler: Produkt von A·B muss eine quadratische Matrix sein" ClrErr Else PassErr EndIf EndTry EndPrgm
|
|
Katalog > |
|
|
tTest m0,Liste[,Häufigkeit[,Hypoth]] (Datenlisteneingabe) tTest m0,x,sx,n,[Hypoth] (Zusammenfassende statistische Eingabe) Führt einen Hypothesen-Test für einen einzelnen, unbekannten Populationsmittelwert m durch, wenn die Populations-Standardabweichung s unbekannt ist. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (Siehe hier.) Getestet wird H0: m = m0 in Bezug auf eine der folgenden Alternativen: Für Ha: m < m0 setzen Sie Hypoth<0 Für Ha: m ƒ m0 (Standard) setzen Sie Hypoth=0 Für Ha: m > m0 setzen Sie Hypoth>0 Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.t |
(x N m0) / (stdev / sqrt(n)) |
|
stat.PVal |
Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann |
|
stat.df |
Freiheitsgrade |
|
stat.x |
Stichprobenmittelwert der Datenfolge in Liste |
|
stat.sx |
Stichproben-Standardabweichung der Datenfolge |
|
stat.n |
Stichprobenumfang |
|
Katalog > |
|
|
tTest_2Samp Liste1,Liste2[,Häufigkeit1[,Häufigkeit2[,Hypoth[,Verteilt]]]] (Datenlisteneingabe) tTest_2Samp v1,sx1,n1,v2,sx2,n2[,Hypoth[,Verteilt]] (Zusammenfassende statistische Eingabe) Berechnet einen t-Test für zwei Stichproben. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (hier.) Getestet wird H0: m1 = m2 in Bezug auf eine der folgenden Alternativen: Für Ha: m1< m2 setzen Sie Hypoth<0 Für Ha: m1ƒ m2 (Standard) setzen Sie Hypoth=0 Für Ha: m1> m2 setzen Sie Hypoth>0 Verteilt=1 verteilt Varianzen Verteilt=0 verteilt keine Varianzen Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
Ausgabevariable |
Beschreibung |
|
stat.t |
Für die Differenz der Mittelwerte berechneter Standardwert |
|
stat.PVal |
Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann |
|
stat.df |
Freiheitsgrade für die t-Statistik |
|
stat.x1, stat.x2 |
Stichprobenmittelwerte der Datenfolgen in Liste 1 und Liste 2 |
|
stat.sx1, stat.sx2 |
Stichproben-Standardabweichungen der Datenfolgen in Liste 1 und Liste 2 |
|
stat.n1, stat.n2 |
Stichprobenumfang |
|
stat.sp |
Die verteilte Standardabweichung. Wird berechnet, wenn Verteilt=1. |
|
Katalog > |
|
|
tvmFV(N,I,PV,Pmt,[PpY],[CpY],[PmtAt])ÞWert Finanzfunktion, die den Geld-Endwert berechnet. Hinweis: Die in den TVM-Funktionen verwendeten Argumente werden in der Tabelle der TVM-Argumente (hier) beschrieben. Siehe auch amortTbl(), hier. |
|
|
Katalog > |
|
|
tvmI(N,PV,Pmt,FV,[PpY],[CpY],[PmtAt])ÞWert Finanzfunktion, die den jährlichen Zinssatz berechnet. Hinweis: Die in den TVM-Funktionen verwendeten Argumente werden in der Tabelle der TVM-Argumente (hier) beschrieben. Siehe auch amortTbl(), hier. |
|
|
Katalog > |
|
|
tvmN(I,PV,Pmt,FV,[PpY],[CpY],[PmtAt])ÞWert Finanzfunktion, die die Anzahl der Zahlungsperioden berechnet. Hinweis: Die in den TVM-Funktionen verwendeten Argumente werden in der Tabelle der TVM-Argumente (hier) beschrieben. Siehe auch amortTbl(), hier. |
|
|
Katalog > |
|
|
tvmPmt(N,I,PV,FV,[PpY],[CpY],[PmtAt])ÞWert Finanzfunktion, die den Betrag der einzelnen Zahlungen berechnet. Hinweis: Die in den TVM-Funktionen verwendeten Argumente werden in der Tabelle der TVM-Argumente (hier) beschrieben. Siehe auch amortTbl(), hier. |
|
|
Katalog > |
|
|
tvmPV(N,I,Pmt,FV,[PpY],[CpY],[PmtAt])ÞWert Finanzfunktion, die den Barwert berechnet. Hinweis: Die in den TVM-Funktionen verwendeten Argumente werden in der Tabelle der TVM-Argumente (hier) beschrieben. Siehe auch amortTbl(), hier. |
|
|
Beschreibung |
Datentyp |
|
|
N |
Anzahl der Zahlungsperioden |
reelle Zahl |
|
I |
Jahreszinssatz |
reelle Zahl |
|
PV |
Barwert |
reelle Zahl |
|
Pmt |
Zahlungsbetrag |
reelle Zahl |
|
FV |
Endwert |
reelle Zahl |
|
PpY |
Zahlungen pro Jahr, Standard=1 |
Ganzzahl > 0 |
|
CpY |
Verzinsungsperioden pro Jahr, Standard=1 |
Ganzzahl > 0 |
|
PmtAt |
Zahlung fällig am Ende oder am Anfang der jeweiligen Zahlungsperiode, Standard=Ende |
Ganzzahl (0=Ende, 1=Anfang) |
* Die Namen dieser TVM-Argumente ähneln denen der TVM-Variablen (z.B. tvm.pv und tvm.pmt), die vom Finanzlöser der Calculator Applikation verwendet werden.Die Werte oder Ergebnisse der Argumente werden jedoch von den Finanzfunktionen nicht unter den TVM-Variablen gespeichert.
|
Katalog > |
|
|
TwoVar X, Y[, [Häuf] [, Kategorie, Mit]] Berechnet die 2-Variablen-Statistik. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (hier.) Alle Listen außer Mit müssen die gleiche Dimension besitzen. X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in Häuf gibt die Häufigkeit für jeden entsprechenden X- und Y-Datenpunkt an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein. Kategorie ist eine Liste von Kategoriecodes für die entsprechenden X und Y Daten. Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten. Ein leeres (ungültiges) Element in einer der Listen X, Freq oder Kategorie führt zu einem Fehler im entsprechenden Element aller dieser Listen. Ein leeres (ungültiges) Element in einer der Listen X1 bis X20 führt zu einem Fehler im entsprechenden Element aller dieser Listen. Weitere Informationen zu leeren Elementen finden Sie (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.v |
Mittelwert der x-Werte |
|
stat.Gx |
Summe der x-Werte |
|
stat.Gx2 |
Summe der x2-Werte |
|
stat.sx |
Stichproben-Standardabweichung von x |
|
stat.sx |
Populations-Standardabweichung von x |
|
stat.n |
Anzahl der Datenpunkte |
|
stat.w |
Mittelwert der y-Werte |
|
stat.Gy |
Summe der y-Werte |
|
stat.Gy2 |
Summe der y2-Werte |
|
stat.sy |
Stichproben-Standardabweichung von y |
|
stat.sy |
Populations-Standardabweichung von y |
|
Stat.Gxy |
Summe der x·y-Werte |
|
stat.r |
Korrelationskoeffizient |
|
stat.MinX |
Minimum der x-Werte |
|
stat.Q1X |
1. Quartil von x |
|
stat.MedianX |
Median von x |
|
stat.Q3X |
3. Quartil von x |
|
stat.MaxX |
Maximum der x-Werte |
|
stat.MinY |
Minimum der y-Werte |
|
stat.Q1Y |
1. Quartil von y |
|
stat.MedY |
Median von y |
|
stat.Q3Y |
3. Quartil von y |
|
stat.MaxY |
Maximum der y-Werte |
|
stat.G(x-v)2 |
Summe der Quadrate der Abweichungen der x-Werte vom Mittelwert |
|
stat.G(y-w)2 |
Summe der Quadrate der Abweichungen der y-Werte vom Mittelwert |