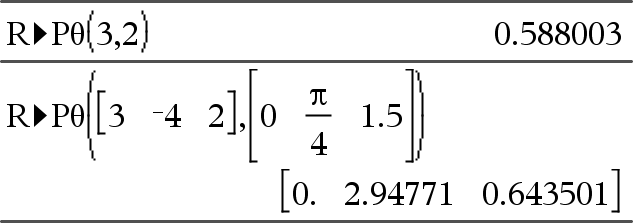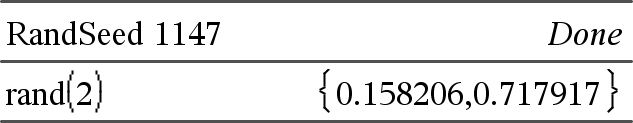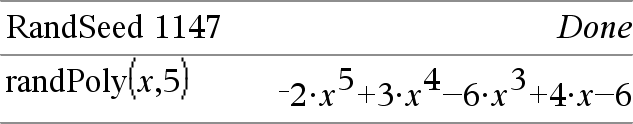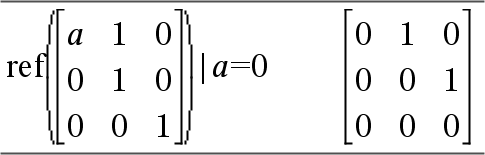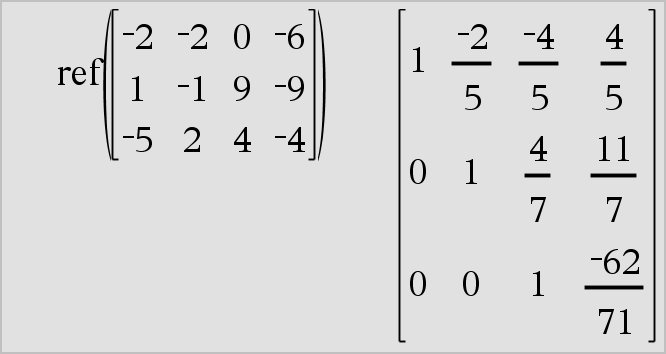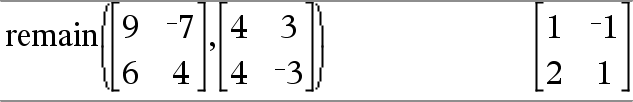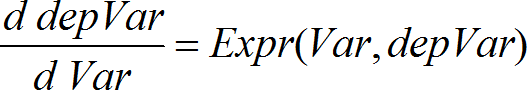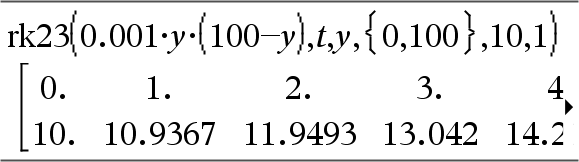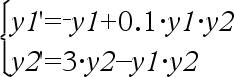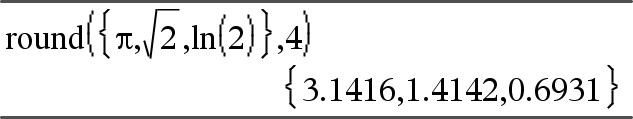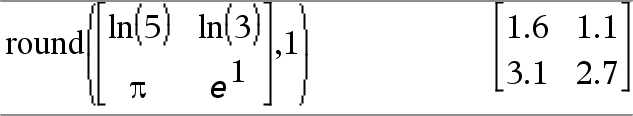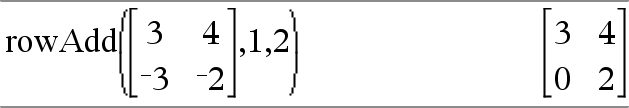|
Katalog > |
|
|
Gibt die äquivalente θ-Koordinate des Hinweis: Das Ergebnis wird gemäß der aktuellen Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie R@Ptheta(...) eintippen. |
Im Grad-Modus:
|
|
Katalog > |
|
|
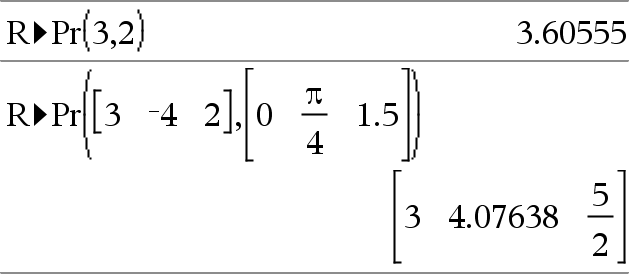
Gibt die äquivalente r-Koordinate des Paars (x,y) zurück. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie R@Pr(...) eintippen. |
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
Wandelt das Argument ins Bogenmaß um. Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @Rad eintippen. |
Im Grad-Modus:
|
|
Katalog > |
|
|
rand() ⇒ Ausdruck rand() gibt einen Zufallswert zwischen 0 und 1 zurück. rand(#Trials) gibt eine Liste zurück, die #Trials Zufallswerte zwischen 0 und 1 enthält. |
Setzt Ausgangsbasis für Zufallszahlengenerierung.
|
|
Katalog > |
|
|
randBin(n, p) ⇒ Ausdruck randBin(n, p) gibt eine reelle Zufallszahl aus einer angegebenen Binomialverteilung zurück. randBin(n, p, #Trials) gibt eine Liste mit #Trials reellen Zufallszahlen aus einer angegebenen Binomialverteilung zurück. |
|
|
Katalog > |
|
|
randInt(lowBound,upBound) ⇒ Ausdruck randInt(lowBound,upBound) gibt eine ganzzahlige Zufallszahl innerhalb der durch UntereGrenze (lowBound) und ObereGrenze (upBound) festgelegten Grenzen zurück. randInt(lowBound,upBound,#Trials) gibt eine Liste mit #Trials ganzzahligen Zufallszahlen innerhalb des festgelegten Bereichs zurück. |
|
|
Katalog > |
|
|
randMat(AnzZeil, AnzSpalt)⇒Matrix Gibt eine Matrix der angegebenen Dimension mit ganzzahligen Werten zwischen -9 und 9 zurück. Beide Argumente müssen zu ganzen Zahlen vereinfachbar sein. |
Hinweis: Die Werte in dieser Matrix ändern sich mit jedem Drücken von ·. |
|
Katalog > |
|
|
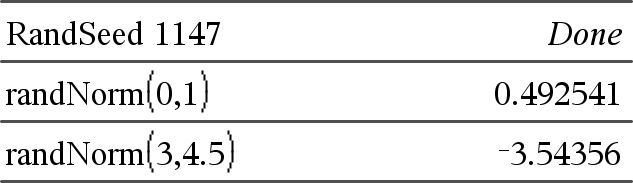
randNorm(μ, σ) ⇒ Ausdruck randNorm(μ, σ) gibt eine Dezimalzahl aus der Gaußschen Normalverteilung zurück. Dies könnte eine beliebige reelle Zahl sein, die Werte konzentrieren sich jedoch stark in dem Intervall [μ−3•σ, μ+3•σ]. randNorm(μ, σ, #Trials) gibt eine Liste mit #Trials Dezimalzahlen aus der angegebenen Normalverteilung zurück. |
|
|
Katalog > |
|
|
randPoly(Var, Ordnung)⇒Ausdruck Gibt ein Polynom in Var der angegebenen Ordnung zurück. Die Koeffizienten sind ganze Zufallszahlen im Bereich −9 bis 9. Der führende Koeffizient ist nicht null. Ordnung muss zwischen 0 und 99 betragen. |
|
|
Katalog > |
|
|
randSamp(List,#Trials[,noRepl])⇒ Liste Gibt eine Liste mit einer Zufallsstichprobe von #Trials Versuchen aus Liste (List) zurück mit der Möglichkeiten, Stichproben zu ersetzen (noRepl=0) oder nicht zu ersetzen (noRepl=1). Die Vorgabe ist mit Stichprobenersatz. |
|
|
Katalog > |
|
|
RandSeed Zahl Zahl = 0 setzt die Ausgangsbasis (“seed”) für den Zufallszahlengenerator auf die Werkseinstellung zurück. Bei Zahl ≠ 0 werden zwei Basen erzeugt, die in den Systemvariablen seed1 und seed2 gespeichert werden. |
|
|
Katalog > |
|
|
real(Value1) ⇒ Wert Gibt den Realteil des Arguments zurück. |
|
|
real(List1) ⇒ Liste Gibt für jedes Element den Realteil zurück. |
|
|
real(Matrix1) ⇒ Matrix Gibt für jedes Element den Realteil zurück. |
|
|
Katalog > |
|
|
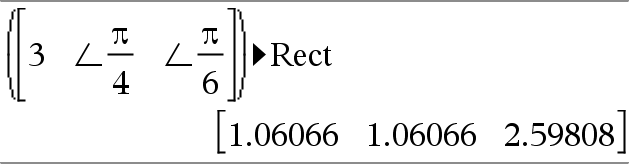
Vektor ►Rect Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @Rect eintippen. Zeigt Vektor in der kartesischen Form [x, y, z] an. Der Vektor muss die Dimension 2 oder 3 besitzen und kann eine Zeile oder eine Spalte sein. Hinweis: ►Rect ist eine Anzeigeformatanweisung, keine Konvertierungsfunktion. Sie können sie nur am Ende einer Eingabezeile benutzen, und sie nimmt keine Aktualisierung von ans vor. Hinweis: Siehe auch ►Polar hier. |
|
|
komplexer Wert ►Rect Zeigt komplexerWert in der kartesischen Form a+bi an. komplexerWert kann jede komplexe Form haben. Eine reiθ-Eingabe verursacht jedoch im Winkelmodus Grad einen Fehler. Hinweis: Für eine Eingabe in Polarform müssen Klammern (r∠θ) verwendet werden. |
Im Bogenmaß-Modus:
Hinweis: Wählen Sie zur Eingabe von ∠ das Symbol aus der Sonderzeichenpalette des Katalogs aus. |
|
Katalog > |
|||||||
|
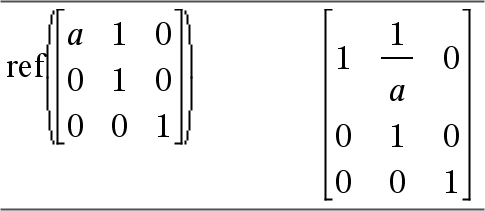
ref(Matrix1[, Tol]) ⇒ Matrix Gibt die Diagonalform von Matrix1 zurück. Sie haben die Option, dass jedes Matrixelement als Null behandelt wird, wenn dessen absoluter Wert geringer als Tol ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Tol ignoriert.
Vermeiden Sie nicht definierte Elemente in Matrix1. Sie können zu unerwarteten Ergebnissen führen. Wenn z. B. im folgenden Ausdruck a nicht definiert ist, erscheint eine Warnmeldung und das Ergebnis wird wie folgt angezeigt:
Die Warnung erscheint, weil das verallgemeinerte Element 1/a für a=0 nicht zulässig wäre. Sie können dieses Problem umgehen, indem Sie zuvor einen Wert in a speichern oder wie im folgenden Beispiel gezeigt eine Substitution mit dem womit-Operator „|“ vornehmen.
Hinweis: Siehe auch rref() here. |
|
|
Katalog > |
|||||||||||
|
RefreshProbeVars Ermöglicht den Zugriff auf Sensordaten von allen verbundenen Sensorsonden in Ihrem TI-Basic-Programm.
|
Beispiel
Hinweis: Dies kann auch mit TI-Innovator™ Hub verwendet werden. |
|
Katalog > |
|
|
Gibt den Rest des ersten Arguments bezüglich des zweiten Arguments gemäß folgender Definitionen zurück: remain(x,0) x |
|
|
Als Folge daraus ist zu beachten, dass remain(−x,y) − remain(x,y). Das Ergebnis ist entweder Null oder besitzt das gleiche Vorzeichen wie das erste Argument. Hinweis: Siehe auch mod() hier. |
|
|
Katalog > |
|||||||||||||||||||
|
Programmierbefehl: Pausiert das Programm und zeigt ein Dialogfeld mit der Meldung promptString sowie einem Eingabefeld für die Antwort des Benutzers an. Wenn der Benutzer eine Antwort eingibt und auf OK klickt, wird der Inhalt des Eingabefelds in die Variable var geschrieben. Falls der Benutzer auf Abbrechen klickt, wird das Programm fortgesetzt, ohne Eingaben zu übernehmen. Das Programm verwendet den vorherigen var-Wert, soweit var bereits definiert wurde. Bei dem optionalen Argument FlagAnz kann es sich um einen beliebigen Ausdruck handeln.
|
Definieren Sie ein Programm: Define request_demo()=Prgm
Starten Sie das Programm und geben Sie eine Antwort ein: request_demo()
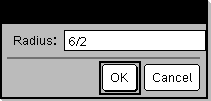
Ergebnis nach Auswahl von OK: Radius: 6/2 |
||||||||||||||||||
|
Das optionale Argument statusVar ermöglicht es dem Programm, zu bestimmen, wie der Benutzer das Dialogfeld verlassen hat. Beachten Sie, dass statusVar das Argument FlagAnz erfordert.
Mit dem Argument func() kann ein Programm die Benutzerantwort als Funktionsdefinition speichern. Diese Syntax verhält sich so, als hätte der Benutzer den folgenden Befehl ausgeführt: Define Fkt(Arg1, ...Argn) = Benutzerantwort Anschließend kann das Programm die so definierte Funktion Fkt() nutzen. Die Meldung EingabeString sollte dem Benutzer die nötigen Informationen geben, damit dieser eine passende Benutzerantwort zur Vervollständigung der Funktionsdefinition eingeben kann. Hinweis: Mit der Option So halten Sie ein Programm an, das einen Befehl Request in einer Endlosschleife enthält:
Hinweis: Siehe auch |
Definieren Sie ein Programm: Define polynomial()=Prgm
Starten Sie das Programm und geben Sie eine Antwort ein: polynomial()
Ergebnis nach Eingabe von x^3+3x+1 und Auswahl von OK: Reelle Wurzeln: {-0,322185} |
|
Katalog > |
|||||||||||||
|
Programmierbefehl: Verhält sich genauso wie die erste Syntax des Befehls Request, die Benutzerantwort wird jedoch immer als String interpretiert. Der Befehl Request interpretiert die Antwort hingegen als Ausdruck, es sei denn, der Benutzer setzt sie in Anführungszeichen (""). Hinweis: Sie können den Befehl RequestStr in benutzerdefinierten Programmen verwenden, jedoch nicht in Funktionen. Zum Anhalten eines Programms mit dem Befehl
Hinweis: Siehe auch |
Definieren Sie ein Programm: Define requestStr_demo()=Prgm
Starten Sie das Programm und geben Sie eine Antwort ein: requestStr_demo()
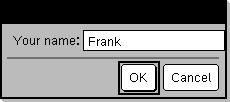
Ergebnis nach Auswahl von OK (Hinweis: Wegen DispFlag = 0 werden Eingabeaufforderung und Antwort nicht im Protokoll angezeigt):
requestStr_demo() Die Antwort hat 5 Zeichen. |
|
Katalog > |
|
|
Return [Ausdr] Gibt Ausdr als Ergebnis der Funktion zurück. Verwendbar in einem Block Func...EndFunc. Hinweis: Verwenden Sie Zurück (Return) ohne Argument innerhalb eines Blocks Prgm...EndPrgm, um ein Programm zu beenden. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
|
|
Katalog > |
|
|
right(Liste1[, Anz]) ⇒ Liste Gibt Anz Elemente zurück, die rechts in Liste1 enthalten sind. Wenn Sie Anz weglassen, wird die gesamte Liste1 zurückgegeben. |
|
|
right(Quellstring[, Anz]) ⇒ string Gibt Anz Zeichen zurück, die rechts in der Zeichenkette Quellstring enthalten sind. Wenn Sie Anz weglassen, wird der gesamte Quellstring zurückgegeben. |
|
|
right(Vergleich) ⇒ Ausdruck Gibt die rechte Seite einer Gleichung oder Ungleichung zurück. |
|
Katalog > |
|
|
Verwendet die Runge-Kutta-Methode zum Lösen des Systems Ausdr ist die rechte Seite, die die gewöhnliche Differentialgleichung (ODE) definiert. AusdrSystem ist ein System rechter Seiten, welche das ODE-System definieren (entspricht der Ordnung abhängiger Variablen in ListeAbhVar). AusdrListe ist eine Liste rechter Seiten, welche das ODE-System definieren (entspricht der Ordnung abhängiger Variablen in ListeAbhVar). Var ist die unabhängige Variable. ListeAbhVar ist eine Liste abhängiger Variablen. {Var0, VarMax} ist eine Liste mit zwei Elementen, die die Funktion anweist, von Var0 zu VarMax zu integrieren. ListeAbhVar0 ist eine Liste von Anfangswerten für abhängige Variablen. Wenn VarSchritt eine Zahl ungleich Null ergibt: Zeichen(VarSchritt) = Zeichen(VarMax-Var0) und Lösungen werden an Var0+i*VarSchritt für alle i=0,1,2,… zurückgegeben, sodass Var0+i*VarSchritt in [var0,VarMax] ist (möglicherweise gibt es keinen Lösungswert an VarMax). Wenn VarSchritt Null ergibt, werden Lösungen an den „Runge-Kutta" Var-Werten zurückgegeben. diftol ist die Fehlertoleranz (standardmäßig 0.001). |
Differentialgleichung: y'=0.001*y*(100-y) und y(0)=10 Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. Dieselbe Gleichung mit diftol auf 1.E−6 Gleichungssystem:
mit y1(0)=2 und y2(0)=5
|
|
Katalog > |
|
|
root(Wert) ⇒ Wurzel
root(Wert1, Wert2) gibt die Wert2 Wurzel von Wert1 zurück. Wert1 kann eine reelle oder komplexe Fließkommakonstante, eine ganze Zahl oder eine komplexe rationale Konstante sein. Hinweis: Siehe auch Vorlage n-te Wurzel, Seite hier. |
|
|
Katalog > |
|
|
rotate(Ganzzahl1[,#Rotationen])⇒ Ganzzahl Rotiert die Bits in einer binären ganzen Zahl. Ganzzahl1 kann mit jeder Basis eingegeben werden und wird automatisch in eine 64-Bit-Dualform konvertiert. Ist der Absolutwert von Ganzzahl1 für diese Form zu groß, wird eine symmetrische Modulo-Operation ausgeführt, um sie in den erforderlichen Bereich zu bringen. Weitere Informationen finden Sie unter ►Base2, hier. |
Im Bin-Modus>
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
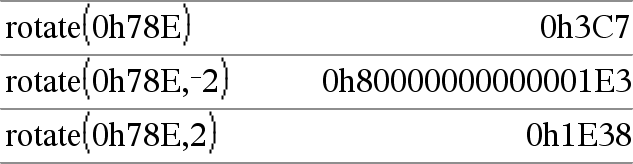
Ist #Rotationen positiv, erfolgt eine Rotation nach links. Ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist −1 (ein Bit nach rechts rotieren). Beispielsweise in einer Rechtsrotation: |
Im Hex-Modus:
|
|
Jedes Bit rotiert nach rechts. 0b00000000000001111010110000110101 Bit ganz rechts rotiert nach ganz links. ergibt sich: 0b10000000000000111101011000011010 Die Ergebnisse werden im jeweiligen Basis-Modus angezeigt. |
Wichtig: Geben Sie eine Dual- oder Hexadezimalzahl stets mit dem Präfix 0b bzw. 0h ein (Null, nicht der Buchstabe O). |
|
rotate(Liste1[,#Rotationen]) ⇒ Liste Gibt eine um #Rotationen Elemente nach rechts oder links rotierte Kopie von Liste1 zurück. Verändert Liste1 nicht. Ist #Rotationen positiv, erfolgt eine Rotation nach links. Ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist −1 (ein Element nach rechts rotieren). |
Im Dec-Modus:
|
|
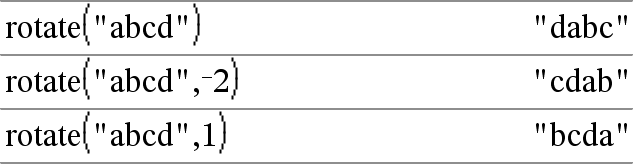
rotate(String1[,#Rotationen]) ⇒ String Gibt eine um #Rotationen Zeichen nach rechts oder links rotierte Kopie von String1 zurück. Verändert String1 nicht. Ist #Rotationen positiv, erfolgt eine Rotation nach links. Ist #Rotationen negativ, erfolgt eine Rotation nach rechts. Vorgabe ist −1 (ein Zeichen nach rechts rotieren) |
|
|
Katalog > |
|
|
round(Wert1[, Stellen]) ⇒ Wert Gibt das Argument gerundet auf die angegebene Anzahl von Stellen nach dem Dezimaltrennzeichen zurück. Stellen muss eine Ganzzahl zwischen 0 und 12 sein. Wenn Stellen nicht eingeschlossen wird, wird das Argument auf 12 Stellen gerundet zurückgegeben. Hinweis: Die Anzeige des Ergebnisses kann von der Einstellung "Angezeigte Ziffern" beeinflusst werden. |
|
|
round(Liste1[, Stellen]) ⇒ Liste Gibt eine Liste von Elementen zurück, die auf die angegebene Stellenzahl gerundet wurden. |
|
|
round(Matrix1[, Stellen]) ⇒ Matrix Gibt eine Matrix von Elementen zurück, die auf die angegebene Stellenzahl gerundet wurden. |
|
|
Katalog > |
|
|
rowAdd(Matrix1, rIndex1, rIndex2) ⇒ Matrix Gibt eine Kopie von Matrix1 zurück, in der die Zeile rIndex2 durch die Summe der Zeilen rIndex1 und rIndex2 ersetzt ist. |
|
|
Katalog > |
|
|
rowDim(Matrix) ⇒ Ausdruck Gibt die Anzahl der Zeilen von Matrix zurück. Hinweis: Siehe auch colDim() hier. |
|
|
Katalog > |
|
|
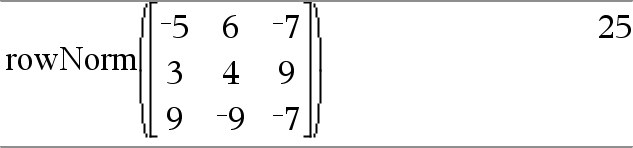
rowNorm(Matrix) ⇒ Ausdruck Gibt das Maximum der Summen der Absolutwerte der Elemente der Zeilen von Matrix zurück. Hinweis: Alle Matrixelemente müssen zu Zahlen vereinfachbar sein. Siehe auch colNorm() hier. |
|
|
Katalog > |
|
|
rowSwap(Matrix1, rIndex1, rIndex2) ⇒ Matrix Gibt Matrix1 zurück, in der die Zeilen rIndex1 und rIndex2 vertauscht sind. |
|
|
Katalog > |
|||||||
|
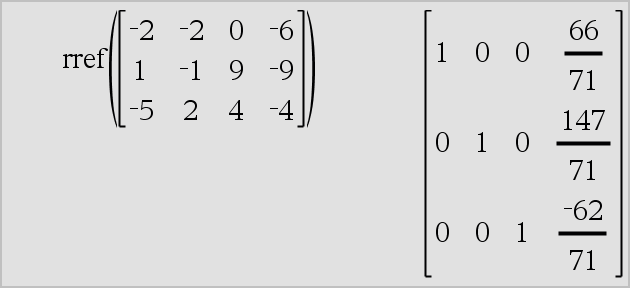
rref(Matrix1[, Tol]) ⇒ Matrix Gibt die reduzierte Diagonalform von Matrix1 zurück. |
|
||||||
|
Sie haben die Option, dass jedes Matrixelement als Null behandelt wird, wenn dessen absoluter Wert geringer als Tol ist. Diese Toleranz wird nur dann verwendet, wenn die Matrix Fließkommaelemente aufweist und keinerlei symbolische Variablen ohne zugewiesene Werte enthält. Anderenfalls wird Tol ignoriert.
Hinweis: Siehe auch ref() here. |