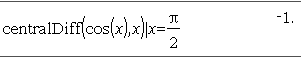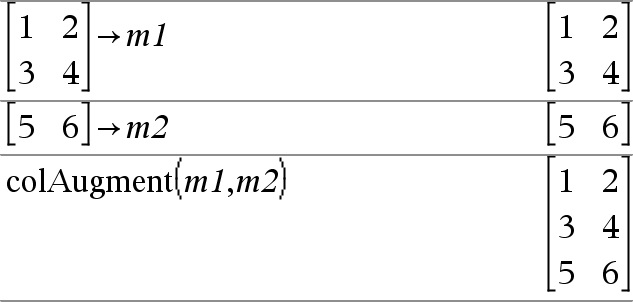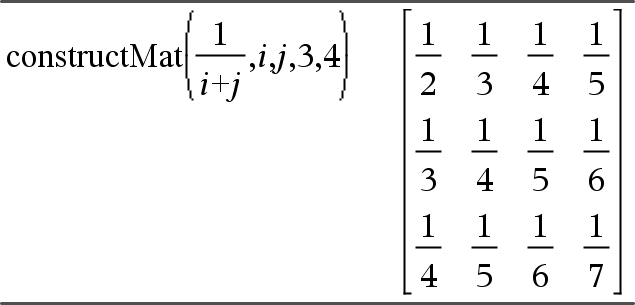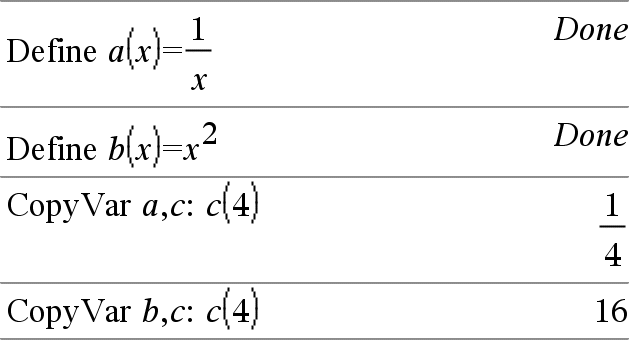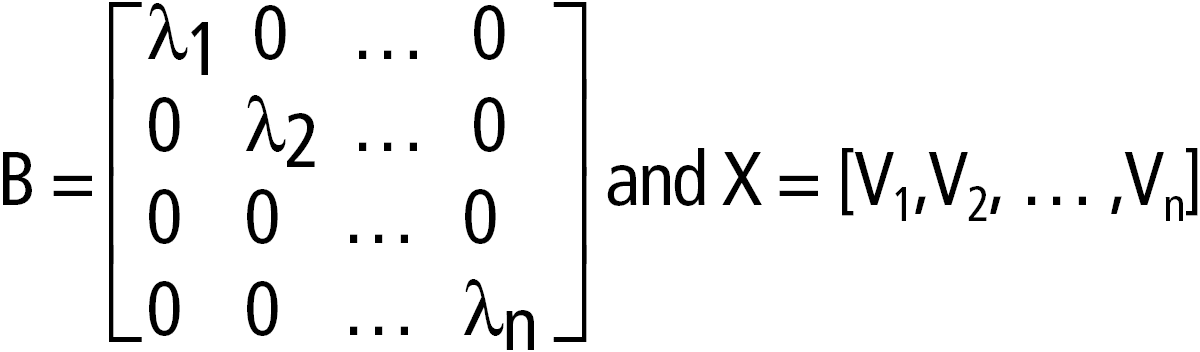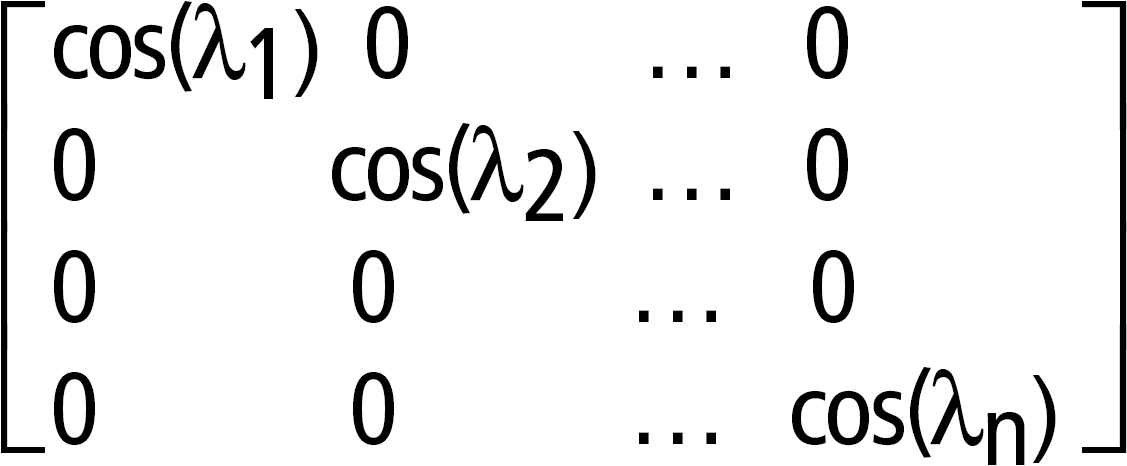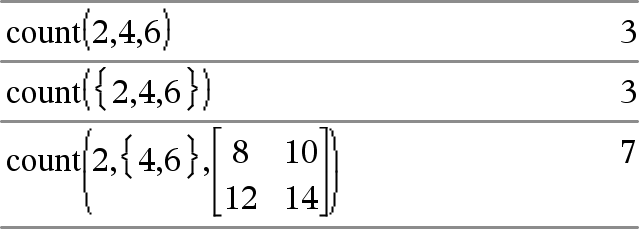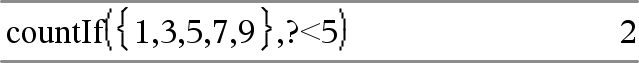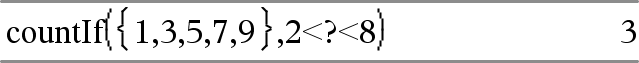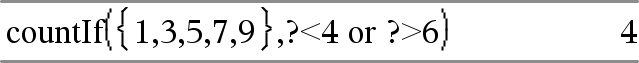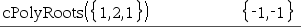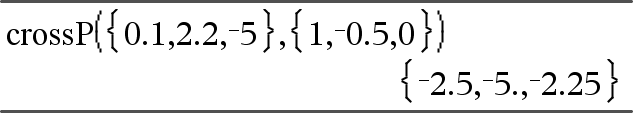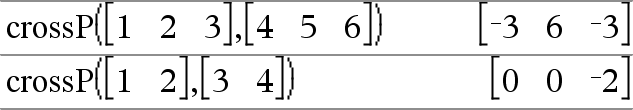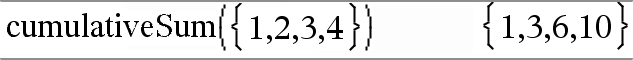|
Katalog > |
|
|
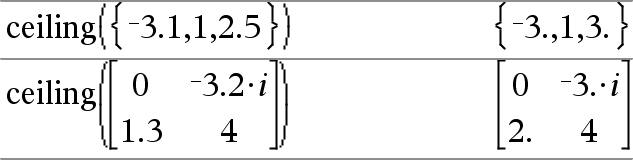
ceiling(Wert1)ÞWert Gibt die erste ganze Zahl zurück, die | dem Argument ist. Das Argument kann eine reelle oder eine komplexe Zahl sein. Hinweis: Siehe auch floor(). |
|
|
ceiling(Liste1)ÞListe ceiling(Matrix1)ÞMatrix Für jedes Element einer Liste oder Matrix wird die kleinste ganze Zahl, die größer oder gleich dem Element ist, zurückgegeben. |
|
|
Katalog > |
|
|
Gibt die numerische Ableitung unter Verwendung des zentralen Differenzenquotienten zurück. Wenn Wert angegeben ist, setzt er jede vorausgegangene Variablenzuweisung oder jede aktuelle „|“ Ersetzung für die Variable außer Kraft. Schritt ist der Schrittwert. Wird Schritt nicht angegeben, wird als Vorgabewert 0,001 benutzt. Wenn Sie Liste1 oder Matrix1 verwenden, wird die Operation über die Werte in der Liste oder die Matrixelemente abgebildet. Hinweis: Siehe auch . |
|
|
Katalog > |
|
|
char(Ganzzahl)ÞZeichen Gibt ein Zeichenstring zurück, das das Zeichen mit der Nummer Ganzzahl aus dem Zeichensatz des Handhelds enthält. Der gültige Wertebereich für Ganzzahl ist 0–65535. |
|
|
Katalog > |
|
|
c22way BeobMatrix chi22way BeobMatrix Berechnet eine c2 Testgröße auf Grundlage einer beobachteten Matrix BeobMatrix. Eine Zusammenfassung der Ergebnisse wird in der Variable stat.results gespeichert. (hier.) Informationen zu den Auswirkungen leerer Elemente in einer Matrix finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.c2 |
Chi-Quadrat-Testgröße: sum(beobachtet - erwartet)2/erwartet |
|
stat.PVal |
Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann |
|
stat.df |
Freiheitsgrade der Chi-Quadrat-Testgröße |
|
stat.ExpMat |
Berechnete Kontingenztafel der erwarteten Häufigkeiten bei Annahme der Nullhypothese |
|
stat.CompMat |
Berechnete Matrix der Chi-Quadrat-Summanden in der Testgröße |
|
Katalog > |
|
|
c2Cdf(untereGrenze,obereGrenze,Freigrad)ÞZahl, wenn untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind chi2Cdf(untereGrenze,obereGrenze,Freiheitsgrad)ÞZahl, wenn untereGrenze und obereGrenze Zahlen sind, Liste, wenn untereGrenze und obereGrenze Listen sind Berechnet die Verteilungswahrscheinlichkeit c2 zwischen untereGrenze und obereGrenze für die angegebenen Freiheitsgrade FreiGrad. Für P(X { obereGrenze) setzen Sie untereGrenze= 0. Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Katalog > |
|
|
c2GOF BeobListe,expListe,FreiGrad chi2GOF BeobListe,expListe,FreiGrad Berechnet eine Testgröße, um zu überprüfen, ob die Stichprobendaten aus einer Grundgesamtheit stammen, die einer bestimmten Verteilung genügt. obsList ist eine Liste von Zählern und muss Ganzzahlen enthalten. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (hier) Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.c2 |
Chi-Quadrat-Testgröße: sum((beobachtet - erwartet)2/erwartet |
|
stat.PVal |
Kleinste Signifikanzebene, bei der die Nullhypothese verworfen werden kann |
|
stat.df |
Freiheitsgrade der Chi-Quadrat-Testgröße |
|
stat.CompList |
Liste der Chi-Quadrat-Summanden in der Testgröße |
|
Katalog > |
|
|
c2Pdf(XWert,FreiGrad)ÞZahl, wenn Xwert eine Zahl ist, Liste, wenn XWert eine Liste ist chi2Pdf(XWert,FreiGrad)ÞZahl, wenn XWert eine Zahl ist, Liste, wenn XWert eine Liste ist Berechnet die Wahrscheinlichkeitsdichtefunktion (Pdf) einer c2-Verteilung an einem bestimmten XWert für die vorgegebenen Freiheitsgrade FreiGrad. Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Katalog > |
|
|
ClearAZ Löscht alle Variablen mit einem Zeichen im aktuellen Problembereich. Wenn eine oder mehrere Variablen gesperrt sind, wird bei diesem Befehl eine Fehlermeldung angezeigt und es werden nur die nicht gesperrten Variablen gelöscht. Siehe |
|
|
Katalog > |
|
|
Löscht den Fehlerstatus und setzt die Systemvariable FehlerCode (errCode) auf Null. Das Else im Block Try...Else...EndTry muss ClrErr oder PassErr (ÜbgebFehler) verwenden. Wenn der Fehler verarbeitet oder ignoriert werden soll, verwenden Sie ClrErr. Wenn nicht bekannt ist, was mit dem Fehler zu tun ist, verwenden Sie PassErr, um ihn an den nächsten Error Handler zu übergeben. Wenn keine weiteren Try...Else...EndTry Error Handler unerledigt sind, wird das Fehlerdialogfeld als normal angezeigt. Hinweis: Siehe auch PassErr, hier, und Try, hier. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
Ein Beispiel für ClrErr finden Sie als Beispiel 2 im Abschnitt zum Befehl Versuche (Try), hier.
|
|
Katalog > |
|
|
colAugment(Matrix1, Matrix2)ÞMatrix Gibt eine neue Matrix zurück, die durch Anfügen von Matrix2 an Matrix1 erzeugt wurde. Die Matrizen müssen gleiche Spaltendimensionen haben, und Matrix2 wird zeilenweise an Matrix1 angefügt. Verändert weder Matrix1 noch Matrix2. |
|
|
Katalog > |
|
|
colDim(Matrix)ÞAusdruck Gibt die Anzahl der Spalten von Matrix zurück. Hinweis: Siehe auch rowDim(). |
|
|
Katalog > |
|
|
colNorm(Matrix)ÞAusdruck Gibt das Maximum der Summen der absoluten Elementwerte der Spalten von Matrix zurück. Hinweis: Undefinierte Matrixelemente sind nicht zulässig. Siehe auch rowNorm(). |
|
|
Katalog > |
|
|
conj(Wert1)ÞWert conj(Liste1)ÞListe conj(Matrix1)ÞMatrix Gibt das komplex Konjugierte des Arguments zurück. Hinweis: Alle undefinierten Variablen werden als reelle Variablen behandelt. |
|
|
Katalog > |
|
|
constructMat(Ausdr,Var1,Var2,AnzZeilen,AnzSpalten) ÞMatrix Gibt eine Matrix auf der Basis der Argumente zurück. Ausdr ist ein Ausdruck in Variablen Var1 und Var2. Die Elemente in der resultierenden Matrix ergeben sich durch Berechnung von Ausdr für jeden inkrementierten Wert von Var1 und Var2. Var1 wird automatisch von 1 bis AnzZeilen inkrementiert. In jeder Zeile wird Var2 inkrementiert von 1 bis AnzSpalten. |
|
|
Katalog > |
|
|
CopyVar Var1, Var2 CopyVar Var1., Var2. CopyVar Var1, Var2 kopiert den Wert der Variablen Var1 auf die Variable Var2 und erstellt ggf. Var2. Variable Var1 muss einen Wert haben. Wenn Var1 der Name einer vorhandenen benutzerdefinierten Funktion ist, wird die Definition dieser Funktion nach Funktion Var2 kopiert. Funktion Var1 muss definiert sein. Var1 muss die Benennungsregeln für Variablen erfüllen oder muss ein indirekter Ausdruck sein, der sich zu einem Variablennamen vereinfachen lässt, der den Regeln entspricht. |
|
|
CopyVar Var1., Var2. kopiert alle Mitglieder der Var1. -Variablengruppe auf die Var2. -Gruppe und erstellt ggf. Var2.. Var1. muss der Name einer bestehenden Variablengruppe sein, wie die Statistikergebnisse stat. nn oder Variablen, die mit der Funktion |
|
|
Katalog > |
|
|
corrMat(Liste1,Liste2[,…[,Liste20]]) Berechnet die Korrelationsmatrix für die erweiterte Matrix [Liste1 Liste2 . . . Liste20]. |
|
|
µ Taste |
|
|
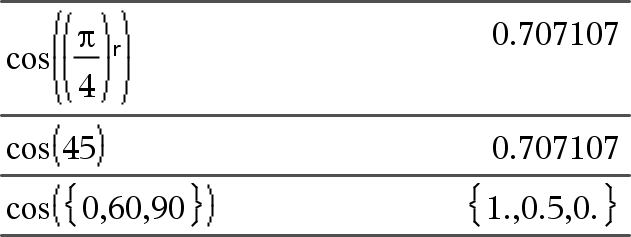
cos(Wert1)ÞWert cos(Liste1)ÞListe
cos(Liste1) gibt in Form einer Liste für jedes Element in Liste1 den Kosinus zurück. Hinweis: Der als Argument angegebene Winkel wird gemäß der aktuellen Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Sie können ¡, G oder R benutzen, um den Winkelmodus vorübergend aufzuheben. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
cos(Quadratmatrix1)ÞQuadratmatrix Gibt den Matrix-Kosinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Kosinus jedes einzelnen Elements. Wenn eine skalare Funktion f(A) auf Quadratmatrix1 (A) angewendet wird, erfolgt die Berechnung des Ergebnisses durch den Algorithmus: Berechnung der Eigenwerte (li) und Eigenvektoren (Vi) von A. Quadratmatrix1 muss diagonalisierbar sein. Sie darf auch keine symbolischen Variablen ohne zugewiesene Werte enthalten. Bildung der Matrizen:
Dann ist A = X B X/und f(A) = X f(B) X/. Beispiel: cos(A) = X cos(B) X/, wobei: cos (B) =
Alle Berechnungen werden unter Verwendung von Fließkomma-Operationen ausgeführt. |
Im Bogenmaß-Modus:
|
|
µ Taste |
|
|
cos/(Wert1)ÞWert cos/(Liste1)ÞListe
cos/(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den inversen Kosinus zurück. Hinweis: Das Ergebnis wird gemäß der aktuellen Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccos(...) eintippen. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
cos/(Quadratmatrix1)ÞQuadratmatrix Gibt den inversen Matrix-Kosinus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Kosinus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
Katalog > |
|
|
cosh(Wert1)ÞWert cosh(Liste1)ÞListe
cosh(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den Cosinus hyperbolicus zurück. |
Im Grad-Modus:
|
|
cosh(Quadratmatrix1)ÞQuadratmatrix Gibt den Matrix-Cosinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des Cosinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
cosh/(Wert1)ÞWert cosh/(Liste1)ÞListe
cosh/(Liste1) gibt in Form einer Liste für jedes Element aus Liste1 den inversen Cosinus hyperbolicus zurück. |
|
|
Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccosh(...) eintippen. cosh/(Quadratmatrix1)ÞQuadratmatrix Gibt den inversen Matrix-Cosinus hyperbolicus von Quadratmatrix1 zurück. Dies ist nicht gleichbedeutend mit der Berechnung des inversen Cosinus hyperbolicus jedes einzelnen Elements. Näheres zur Berechnungsmethode finden Sie im Abschnitt cos(). Quadratmatrix1 muss diagonalisierbar sein. Das Ergebnis enthält immer Fließkommazahlen. |
Im Winkelmodus Bogenmaß und Komplex-Formatmodus “kartesisch”:
Um das ganze Ergebnis zu sehen, drücken Sie 5 und verwenden dann 7 und 8, um den Cursor zu bewegen. |
|
µ Taste |
|
|
cot(Wert1) Þ Wert cot(Liste1) Þ Liste Gibt den Kotangens von Wert1 oder eine Liste der Kotangens aller Elemente in Liste1 zurück. Hinweis: Der als Argument angegebene Winkel wird gemäß der aktuellen Winkelmoduseinstellung als Grad, Neugrad oder Bogenmaß interpretiert. Sie können ¡, G oder R benutzen, um den Winkelmodus vorübergend aufzuheben. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
µ Taste |
|
|
cot/(Wert1)ÞWert cot/(Liste1)ÞListe Gibt entweder den Winkel, dessen Kotangens Wert1 ist, oder eine Liste der inversen Kotangens aller Elemente in Liste1 zurück. Hinweis: Das Ergebnis wird gemäß der aktuellen Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccot(...) eintippen. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
coth(Wert1)ÞWert coth(Liste1)ÞListe
|
|
|
Katalog > |
|
|
coth/(Wert1)ÞWert coth/(Liste1)ÞListe Gibt den inversen hyperbolischen Kotangens von Wert1 oder eine Liste der inversen hyperbolischen Kotangens aller Elemente in Liste1 zurück. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccoth(...) eintippen. |
|
|
Katalog > |
|
|
count(Wert1oderListe1 [,Wert2oderListe2 [,...]])ÞWert Gibt die kumulierte Anzahl aller Elemente in den Argumenten zurück, deren Auswertungsergebnisse numerische Werte sind. Jedes Argument kann ein Ausdruck, ein Wert, eine Liste oder eine Matrix sein. Sie können Datenarten mischen und Argumente unterschiedlicher Dimensionen verwenden. Für eine Liste, eine Matrix oder einen Zellenbereich wird jedes Element daraufhin ausgewertet, ob es in die Zählung eingeschlossen werden soll. Innerhalb der Lists & Spreadsheet Applikation können Sie anstelle eines beliebigen Arguments auch einen Zellenbereich verwenden. Leere (ungültige) Elemente werden ignoriert. Weitere Informationen zu leeren Elementen finden Sie (hier). |
|
|
Katalog > |
|||||||
|
countIf(Liste,Kriterien)ÞWert Gibt die kumulierte Anzahl aller Elemente in der Liste zurück, die die festgelegten Kriterien erfüllen. Kriterien können sein:
Innerhalb der Lists & Spreadsheet Applikation können Sie anstelle der Liste auch einen Zellenbereich verwenden. Leere (ungültige) Elemente in der Liste werden ignoriert. Weitere Informationen zu leeren Elementen finden Sie (hier). |
Zählt die Anzahl der Elemente, die 3 entsprechen.
Zählt die Anzahl der Elemente, die “def.” entsprechen
Zählt 1 und 3.
Zählt 3, 5 und 7.
Zählt 1, 3, 7 und 9. |
|
Katalog > |
|
|
Die erste Syntax
Die zweite Syntax Hinweis: Siehe auch |
|
|
Katalog > |
|
|
crossP(Liste1, Liste2)ÞListe Gibt das Kreuzprodukt von Liste1 und Liste2 als Liste zurück. Liste1 und Liste2 müssen die gleiche Dimension besitzen, die entweder 2 oder 3 sein muss. |
|
|
crossP(Vektor1, Vektor2)ÞVektor Gibt einen Zeilen- oder Spaltenvektor zurück (je nach den Argumenten), der das Kreuzprodukt von Vektor1 und Vektor2 ist. Entweder müssen Vektor1 und Vektor2 beide Zeilenvektoren oder beide Spaltenvektoren sein. Beide Vektoren müssen die gleiche Dimension besitzen, die entweder 2 oder 3 sein muss. |
|
|
µ Taste |
|
|
csc(Wert1)ÞWert csc(Liste1)ÞListe
|
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
µ Taste |
|
|
csc/(Wert1) Þ Wert csc/(Liste1) Þ Liste Gibt entweder den Winkel, dessen Kosekans Wert1 entspricht, oder eine Liste der inversen Kosekans aller Elemente in Liste1 zurück. Hinweis: Das Ergebnis wird gemäß der aktuellen Winkelmoduseinstellung in Grad, in Neugrad oder im Bogenmaß zurückgegeben. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccsc(...) eintippen. |
Im Grad-Modus:
Im Neugrad-Modus:
Im Bogenmaß-Modus:
|
|
Katalog > |
|
|
csch(Wert1) Þ Wert csch(Liste1) Þ Liste
|
|
|
Katalog > |
|
|
csch/(Wert1) Þ Wert csch/(Liste1) Þ Liste Gibt den inversen hyperbolischen Kosekans von Wert1 oder eine Liste der inversen hyperbolischen Kosekans aller Elemente in Liste1 zurück. Hinweis: Sie können diese Funktion über die Tastatur Ihres Computers eingeben, indem Sie arccsch(...) eintippen. |
|
|
Katalog > |
|
|
CubicReg X, Y[, [Häuf] [, Kategorie, Mit]] Berechnet die kubische polynomiale Regressiony = a·x3+b· x2+c·x+dauf Listen X und Y mit der Häufigkeit Häuf. Eine Zusammenfassung der Ergebnisse wird in der Variablen stat.results gespeichert. (hier.) Alle Listen außer Mit müssen die gleiche Dimension besitzen. X und Y sind Listen von unabhängigen und abhängigen Variablen. Häuf ist eine optionale Liste von Häufigkeitswerten. Jedes Element in Häuf gibt die Häufigkeit für jeden entsprechenden Datenpunkt X und Y an. Der Standardwert ist 1. Alle Elemente müssen Ganzzahlen | 0 sein. Kategorie ist eine Liste von Kategoriecodes Mit ist eine Liste von einem oder mehreren Kategoriecodes. Nur solche Datenelemente, deren Kategoriecode in dieser Liste enthalten ist, sind in der Berechnung enthalten. Informationen zu den Auswirkungen leerer Elemente in einer Liste finden Sie unter “Leere (ungültige) Elemente” (hier). |
|
|
Ausgabevariable |
Beschreibung |
|
stat.RegEqn |
Regressionsgleichung: a·x3+b·x2+c·x+d |
|
stat.a, stat.b, stat.c, stat.d |
Regressionskoeffizienten |
|
stat.R2 |
Bestimmungskoeffizient |
|
stat.Resid |
Residuen von der Regression |
|
stat.XReg |
Liste der Datenpunkte in der modifizierten X List, die schließlich in der Regression mit den Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde |
|
stat.YReg |
Liste der Datenpunkte in der modifizierten Y List, die schließlich in der Regression mit den Beschränkungen für Häufigkeit, Kategorieliste und Mit Kategorien verwendet wurde |
|
stat.FreqReg |
Liste der Häufigkeiten für stat.XReg und stat.YReg |
|
Katalog > |
|
|
cumulativeSum(Liste1)ÞListe Gibt eine Liste der kumulierten Summen der Elemente aus Liste1 zurück, wobei bei Element 1 begonnen wird. |
|
|
cumulativeSum(Matrix1)ÞMatrix Gibt eine Matrix der kumulierten Summen der Elemente aus Matrix1 zurück. Jedes Element ist die kumulierte Summe der Spalte von oben nach unten. Ein leeres (ungültiges) Element in Liste1 oder Matrix1 erzeugt ein ungültiges Element in der resultierenden Liste oder Matrix. Weitere Informationen zu leeren Elementen finden Sie (hier). |
|
|
Katalog > |
|
|
Cycle (Zyklus) Übergibt die Programmsteuerung sofort an die nächste Wiederholung der aktuellen Schleife (For, While oder Loop). Cycle ist außerhalb dieser drei Schleifenstrukturen (For, While oder Loop) nicht zulässig. Hinweis zum Eingeben des Beispiels: Anweisungen für die Eingabe von mehrzeiligen Programm- und Funktionsdefinitionen finden Sie im Abschnitt „Calculator“ des Produkthandbuchs. |
Funktionslisting, das die ganzen Zahlen von 1 bis 100 summiert und dabei 50 überspringt.
|
|
Katalog > |
|
|
Vektor 4Cylind Hinweis: Sie können diesen Operator über die Tastatur Ihres Computers eingeben, indem Sie @>Cylind eintippen. Zeigt den Zeilen- oder Spaltenvektor in Zylinderkoordinaten [r,±q, z] an. Vektor muss genau drei Elemente besitzen. Er kann entweder ein Zeilen- oder Spaltenvektor sein. |
|