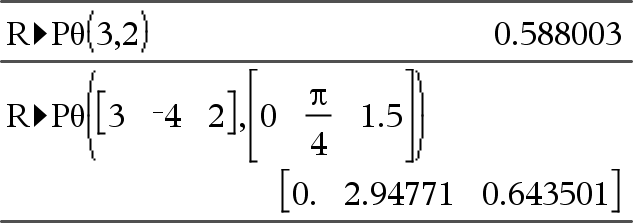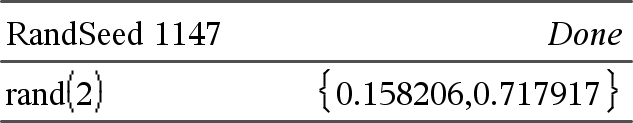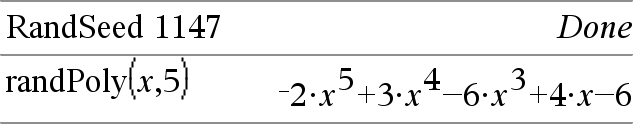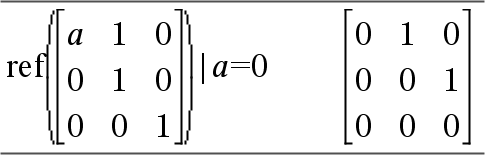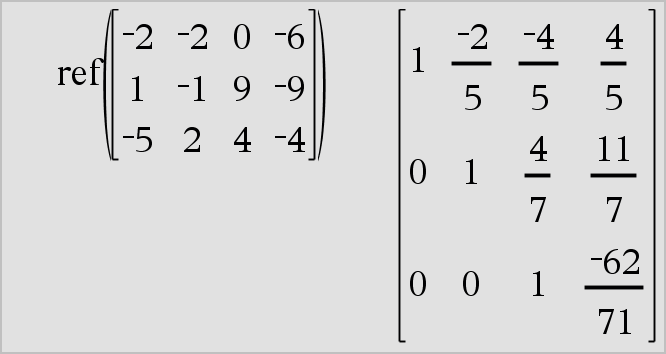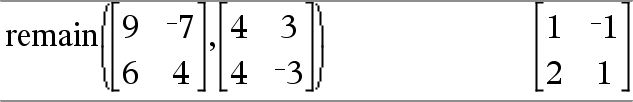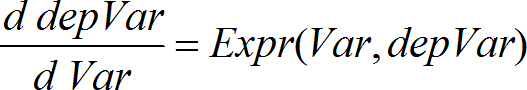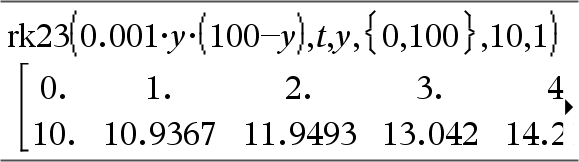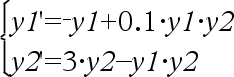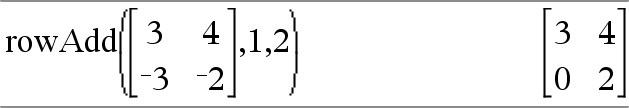R

R►Pθ()

Katalog >


R►Pθ (xValue, yValue) ⇒ værdi
R►Pθ (xList, yList) ⇒ liste
R►Pθ (xMatrix, yMatrix) ⇒ matrix

Returnerer den ækvivalente θ-koordinat for
(x,y) argumentparret.

Bemærk: Resultatet returneres som en vinkel i grader, nygrader eller radian afhængig af den aktuelle vinkeltilstand.

Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive R@>Ptheta(...).

I vinkeltilstanden Grader:


I vinkeltilstanden Nygrader:


I vinkeltilstanden Radian:

R►Pr()

Katalog >


R►Pr (xValue, yValue) ⇒ værdi
R►Pr (xList, yList) ⇒ liste
R►Pr (xMatrix, yMatrix) ⇒ matrix

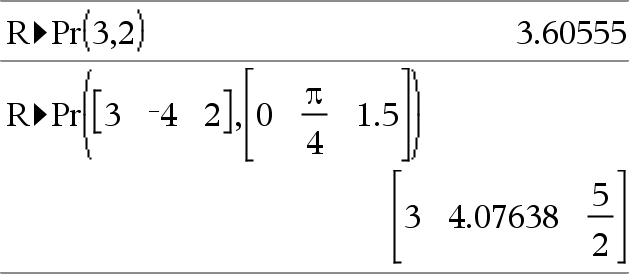
Returnerer den ækvivalente r-koordinat for (x,y) argumentparret.

Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive R@>Pr(...).

I vinkeltilstanden Radian:

►Rad

Katalog >

Value1►Rad ⇒ værdi

Konverterer argumentet til vinkelmåling i radian.

Bemærk: Du kan indsætte denne operator fra computerens tastatur ved at skrive @>Rad.

I vinkeltilstanden grader:


I vinkeltilstanden Nygrader:

rand()

Katalog >

rand() ⇒ udtryk
rand(#Trials) ⇒ liste

rand() returnerer en vilkårlig værdi mellem 0 og 1.

rand(#Trials) returnerer en liste med #Trials vilkårlig værdier mellem 0 og 1.

Angiv seed-værdien for et vilkårligt tal.

randBin()

Katalog >

randBin(n, p) ⇒ udtryk
randBin(n, p, #Trials) ⇒ liste

randBin(n, p) returnerer et vilkårlig reelt tal fra en given binomialfordeling.

randBin(n, p, #Trials) returnerer en liste med #Trials vilkårlige reelle tal fra en given binomialfordeling.

randInt()

Katalog >

randInt(lowBound,upBound) ⇒ udtryk
randInt(lowBound,upBound ,#Trials) ⇒ liste

randInt(lowBound,upBound) returnerer et vilkårligt heltal i det område, der angives af heltalsgrænserne lowBound og upBound.

randInt(lowBound,upBound ,#Trials) returnerer en liste med #Trials vilkårlige heltal i det angivne område.

randMat()

Katalog >

randMat(numRows, numColumns) ⇒ matrice

Returnerer en matrix med heltal mellem -9 og 9 af den angivne dimension.

Begge argumenter skal kunne reduceres til heltal.

Bemærk: Værdierne i denne matrix ændres, hver gang du trykker .

randNorm()

Katalog >

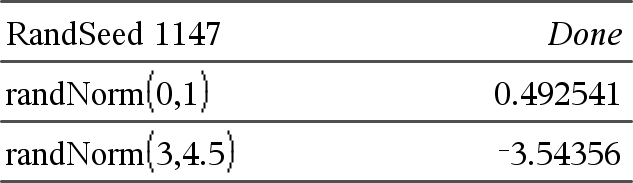
randNorm(μ, σ) ⇒ udtryk
randNorm(μ, σ, #Trials) ⇒ liste

randNorm(μ, σ) returnerer et decimalt tal fra den angivne normalfordeling. Det kan være ethvert reelt tal, men vil være kraftigt koncentreret i intervallet [μ−3•σ, μ+3•σ].

randNorm(μ, σ, #Trials) returnerer en liste med #Trials decimaltal fra den angivne normalfordeling.

randPoly()

Katalog >

randPoly(Var, Order) ⇒ udtryk

Returnerer et polynomium i Var af den angivne Order. Koefficienterne er vilkårlige heltal i området −9 til 9. Koefficienten af højeste grad vil ikke være nul.

Order skal være 0–99.

randSamp()

Katalog >

randSamp(List,#Trials[,noRepl]) ⇒ liste

Returnerer en liste med en vilkårlig stikprøve af #Trials målinger fra List med mulighed for tilbagelægning (noRepl=0) eller ingen tilbagelægning (noRepl=1). Standardindstillingen er med tilbagelægning.

RandSeed

Katalog >

RandSeed Number

Hvis Number = 0, indstilles startværdien til fabriksindstillingerne for vilkårlig-tal-generatoren. Hvis Number ≠ 0, anvendes det til at generere to startværdier, der lagres i systemvariablerne seed1 og seed2.

real()

Katalog >

real(Value1) ⇒ værdi

Returnerer den reelle del af argumentet.

real(List1) ⇒ liste

Returnerer realdelen af alle elementer.

real(Matrix1) ⇒ matrix

Returnerer realdelen af alle elementer.

►Rect

Katalog >

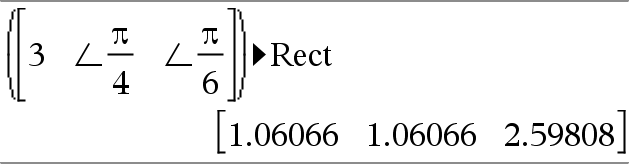
Vektor ►Rect

Bemærk: Du kan indsætte denne operator fra computerens tastatur ved at skrive @>Rect.

Viser Vektor i rektangulær form [x, y, z]. Vektoren skal være af dimensionen 2 eller 3 og kan være en række eller kolonne.

Bemærk: ►Rect er en displayformatkommando, ikke en konverteringsfunktion. Du kan kun anvende den i slutningen af en indtastningslinje, og den opdaterer ikke ans.

Bemærk: Se også ►Polær ligning, her.

complexValue ►Rect

Viser complexValue i rektangulær form a+bi. complexValue kan have enhver kompleks form. Men en reiθ-indtastning udløser en fejl i vinkeltilstanden Grader.

Bemærk: Du skal anvende parenteser til en (r∠θ) polær indtastning.

I vinkeltilstanden Radian:


I vinkeltilstanden Nygrader:


I vinkeltilstanden grader:

Bemærk: Du kan skrive ∠ ved at vælge det i symbollisten i kataloget.

ref()

Katalog >

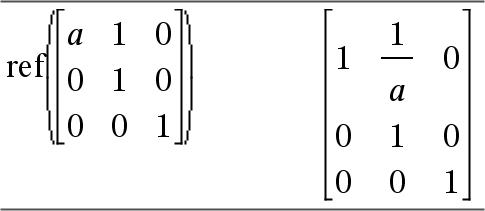
ref(Matrix1[, Tol]) ⇒ matrix

Returnerer række-echelonformen af Matrix1.

Ethvert matrixelement kan valgfrit behandles som nul, hvis dets absolutte værdi er mindre end Tol. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke har fået tildelt en værdi. Ellers ignoreres Tol.

• Hvis du anvender /·· eller indstiller Auto- eller Approximate -tilstanden til Approximate, foretages beregningerne med flydende komma.
• Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Undgå udefinerede elementer i Matrix1. De kan føre til uventede resultater.

Hvis for eksempel a er udefineret i følgende udtryk, vil en advarsel blive vist, og resultatet vises som:

Advarslen vises, fordi det generaliserede element 1/a ikke ville være gyldig for a=0.

Du kan undgå dette ved i forvejen at gemme en værdi tila eller ved at bruge betingelsesoperatoren (“|”) til at substituere en værdi som vist i følgende eksempel.

Bemærk: Se også rref(), here.

 

RefreshProbeVars

Katalog >

RefreshProbeVars

Giver dig adgang til sensordata fra alle tilkoblede sensorprober i dit TI-Basic-program.

StatusVar-værdi

Status

statusVar=0

Normal (fortsæt med programmet)

statusVar=1

Vernier DataQuest™-applikation er i dataindsamlingstilstand.

Bemærk: Vernier DataQuest™-applikation skal være i målertilstand for at denne kommando virker.

statusVar=2

Vernier DataQuest™-applikation blev ikke startet.

statusVar=3

Vernier DataQuest™-applikationen blev startet, men du har ikke tilkoblet nogen prober.

Eksempel

Define temp()=

Prgm

© Tjek, om systemet er klar

RefreshProbeVars-status

If status=0 Then

Disp "klar"

For n,1,50

RefreshProbeVars-status

temperatur:=meter.temperatur

Disp "Temperatur: ",temperatur

If temperature>30 Then

Disp "For varmt"

EndIf

© Vent i 1 sekund mellem stikprøver

Wait 1

EndFor

Else

Disp "Ikke klar. Prøv igen senere"

EndIf

EndPrgm

 

Bemærk: Dette kan også bruge med TI-Innovator™-hubben.

 

remain()

Katalog >


remain(Value1, Value2) ⇒ værdi
remain(List1, List2) ⇒ liste
remain(Matrix1, Matrix2) ⇒ matrix

Returnerer resten af det første argument med hensyn til det andet argument som defineret af identiteterne:

remain(x,0)   x
remain(x,y)   x−y•iPart(x/y)

Bemærk, at som følge heraf, remain(−x,y) − remain(x,y). Resultatet er enten nul, eller det har samme fortegn som det første argument.

Bemærk: Se også mod(), her.

Request

Katalog >

Request promptString, var[, DispFlag [, statusVar]]

Request promptString, func(arg1, ...argn)  [, DispFlag [, statusVar]]

Programmeringskommando: Standser programmet midlertidigt og viser en dialogboks med meddelelsen promptString og et indtastningsfelt til brugerens svar.

Når brugeren skriver et svar og klikker på OK, tildeles indtastningsfeltets indhold til variablen var.

Hvis brugeren klikker på Annuller, fortsætter programmet uden at acceptere noget input. Programmet bruger den tidligere værdi for var hvis var var defineret i forvejen.

Det valgfrie argument DispFlag kan være et hvilket som helst udtryk.

• Hvis DispFlag er udelades eller evalueres til 1, vil klarmeddelelsen og brugerens svar blive vist i beregnerens historik.
• Hvis DispFlag evalueres til 0, vil klarmeddelelsen og svaret ikke blive vist historikken.

Definer et program:

Define request_demo()=Prgm
    Request “Radius: ”,r
    Disp “Areal = “,pi*r2
EndPrgm

 

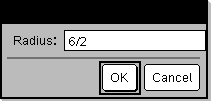
Start programmet, og indtast et svar:

request_demo()

Resultat efter valg af OK:

Radius: 6/2
Areal = 28,2743

Det valgfri argument statusVar gør det muligt for programmet at bestemme, hvordan brugeren forlod dialogboksen. Bemærk, at statusVar kræver argumentet DispFlag.

• Hvis brugeren klikkede OK eller trykkede på Enter eller Ctrl+Enter, indstilles variablen statusVar til en værdi på 1.
• I modsat fald indstilles variablen statusVar til en værdi på 0.

Med argumentet func() kan et program lagre brugerens svar som en funktionsdefinition. Denne syntaks virker, ligesom hvis brugeren udførte kommandoen:

     Define func(arg1, ...argn) = brugers svar

Så kan programmet bruge den definerede funktion func(). promptString bør vejlede brugeren til at indtaste en passende brugers svar, der fuldender funktionsdefinitionen.

Bemærk: Du kan bruge kommandoen Request i et brugerdefineret program, men ikke i en funktion.

Sådan stoppes et program, der indeholder kommandoen Request i en uendelig løkke:

• Håndholdt: Hold tasten c nede, mens du gentagne gange trykker på ·.
• Windows®: Hold tasten F12 nede, mens du gentagne gange trykker på Enter.
• Macintosh®: Hold tasten F5 nede, mens du gentagne gange trykker på Enter.
• iPad®: App'en viser en meddelelse. Du kan fortsat vente eller annullere.

Bemærk: Se også RequestStr, here.

Definer et program:

Define polynomial()=Prgm
    Request "Indtast et polynomium i x:",p(x)
    Disp "Reelle rødder er:",polyRoots(p(x),x)
EndPrgm

 

Start programmet, og indtast et svar:

polynomium()

Resultat efter indtastning af x^3+3x+1 og valg af OK:

Reelle rødder er: {-0.322185}

RequestStr

Katalog >

RequestStr promptString, var[, DispFlag]

Programmeringskommando: Fungerer identisk med den første syntaks i kommandoen Request, bortset fra at brugerens svar altid fortolkes som en streng. I modsætning hertil fortolker kommandoen Request svarene som et udtryk, medmindre brugeren omslutter det med citationstegn ("").

Bemærk: Du kan bruge kommandoen RequestStr i et brugerdefineret program, men ikke i en funktion.

Sådan standses et program, der indeholder en RequestStr kommando i en uendelig løkke:

• Håndholdt: Hold tasten c nede, mens du gentagne gange trykker på ·.
• Windows®: Hold tasten F12 nede, mens du gentagne gange trykker på Enter.
• Macintosh®: Hold tasten F5 nede, mens du gentagne gange trykker på Enter.
• iPad®: App'en viser en meddelelse. Du kan fortsat vente eller annullere.

Bemærk: Se også Request, here.

Definer et program:

Define requestStr_demo()=Prgm
    RequestStr “Dit navn:”,name,0
    Disp “Svaret har “,dim(name),” tegn.”
EndPrgm

 

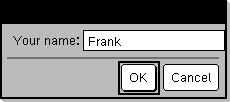
Start programmet, og indtast et svar:

requestStr_demo()

 

Resultat efter valg af OK (Bemærk, at argumentet DispFlag fra 0 udelader klarmeddelelsen og svaret fra historikken):

 

requestStr_demo()

Svaret har fem tegn.

Return

Katalog >

Return [Expr]

Returnerer Expr som resultatet af funktionen. Bruges i en Func...EndFunc-blok.

Bemærk: Brug Return uden et argument med en Prgm...EndPrgm-blok for at lukke et program.

Bemærk indtastning af eksemplet: For instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

right()

Katalog >

right(List1[, Num]) ⇒ liste

Returnerer Num-elementer længst til højre i List1.

Hvis du udelader Num, returneres hele List1.

right(sourceString[, Num]) ⇒ string

Returnerer Num-tegn længst til højre i tegnstrengen sourceString.

Hvis du udelader Num, returneres hele sourceString.

right(Comparison) ⇒ udtryk

Returnerer højre side af en ligning eller ulighed.

rk23 ()

Katalog >

rk23(Expr, Var, depVar, {Var0, VarMax}, depVar0, VarStep [, diftol]) ⇒ matrix

rk23(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

rk23(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

Anvender Runge-Kutta-metoden til at løse systemet

med depVar(Var0)=depVar0 i intervallet [Var0,VarMax]. Returnerer en matrix, hvor første række definerer Var-outputværdierne som defineret af VarStep. Den anden række definerer værdien af den første løsningskomponent i de tilsvarende Var-værdier, osv.

Expr er højresiden, som definerer den ordinære differentialligning (ODE - ordinary differential equation).

SystemOfExpr er et system af højresider, der definerer ODE'erne (svarende til rækkefølgen af afhængige variable i ListOfDepVars).

ListOfExpr er en liste af højresider, der definerer systemet af ODE'er (svarende til rækkefølgen af afhængige variable i ListOfDepVars).

Var er den uafhængige variabel.

ListOfDepVars er en liste med afhængige variabler.

{Var0, VarMax} er en liste med to elementer, der informerer funktionen om at integrere fra Var0 til VarMax.

ListOfDepVars0 er en liste af oprindelige værdier for afhængige variabler.

Hvis VarStep evalueres til et tal forskelligt fra nul: sign(VarStep) = sign(VarMax-Var0) og løsninger returneres ved Var0+i*VarStep for alle i=0,1,2,… således at Var0+i*VarStep er i [var0,VarMax] (der vil muligvis ikke være en løsningsværdi ved VarMax).

Hvis VarStep evalueres til nul, returneres løsningerne i "Runge-Kutta" Var-værdier.

diftol er fejltolerancen (som standard 0.001).

Differentialligning:

y'=0.001*y*(100-y) og y(0)=10

Du kan se hele resultatet ved at trykke på 5 og derefter bruge 7 og 8 til at bevæge markøren.

Samme ligning med diftol sat til 1.E−6

System af ligninger:

med y1(0)=2 og y2(0)=5

root()

Katalog >

root(Value) ⇒ rod
root(Value1, Value2) ⇒ rod

root(Value) returnerer kvadratroden af Value.

root(Value1, Value2) returnerer denValue2-te​​​-rod af Value1. Value1 kan være en reel eller kompleks konstant med flydende decimaler eller et heltal eller en kompleks rational konstant.

Bemærk: Se også N-te rod-skabelon, her.

rotate()

Katalog >

rotate(Integer1[,#ofRotations]) ⇒ heltal

Roterer bittene i et binært heltal. Du kan indtaste Integer1 i ethvert talsystem; det konverteres automatisk til en 64-bit binær form med fortegn. Hvis Integer1 er for stort til denne form, bringer en symmetrisk modulo-operation værdien ind i det korrekte område. Der er flere oplysninger under ►Base2,  her.

I binær tilstand:

 

Du kan se hele resultatet ved at trykke på 5 og derefter bruge 7 og 8 til at bevæge markøren.

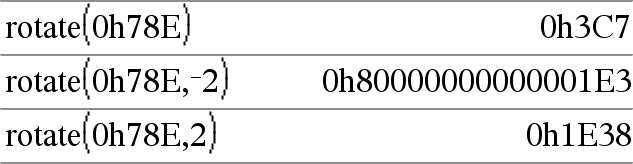
Hvis #ofRotations er positivt, kører rotationen mod venstre. Hvis #ofRotations er negativt, kører rotationen mod højre. Standardindstillingen er −1 (rotér en bit til højre).

For eksempel i en højrerotation:

I hexadecimal tilstand:

Hver bit roterer til højre.

0b00000000000001111010110000110101

Bitten længst til højre roterer længst mod venstre.

giver:

0b10000000000000111101011000011010

Resultatet vises i den valgte tilstand for talsystem.

Vigtigt: Til binære eller hexadecimale indtastninger skal du som præfiks altid benytte henholdsvis 0b eller 0h (nul, ikke bogstavet O).

rotate(List1[,#ofRotations]) ⇒ liste

Returnerer en kopi af List1 roteret til højre eller venstre med #of Rotations-elementer. Ændrer ikke List1.

Hvis #ofRotations er positivt, kører rotationen mod venstre. Hvis #of Rotations er negativt, kører rotationen mod højre. Standardindstillingen er −1 (roter en bit til højre).

I decimal tilstand:

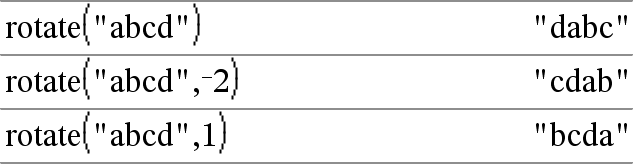
rotate(String1[,#ofRotations]) ⇒ string

Returnerer en kopi af String1 roteret til højre eller venstre med  #ofRotations-tegn. Ændrer ikke String1.

Hvis #ofRotations er positivt, kører rotationen mod venstre. Hvis #ofRotations er negativt, kører rotationen mod højre. Standardindstillingen −1 (rotér en bit til højre).

round()

Katalog >

round(Value1[, digits]) ⇒ værdi

Returnerer argumentet afrundet til det angivne antal cifre efter decimalpunktet.

digits skal være et heltal i området 0–12. Hvis digits ikke er inkluderet, returneres argumentet afrundet til 12 væsentlige cifre.

Bemærk: Vis cifre-tilstanden kan påvirke den måde, dette vises på.

round(List1[, digits]) ⇒ liste

Returnerer en liste med elementerne afrundet til det angivne antal cifre.

round(Matrix1[, digits]) ⇒ matrix

Returnerer en matrix med elementerne afrundet til det angivne antal cifre.

rowAdd()

Katalog >

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ matrix

Returnerer en kopi af Matrix1 med rækken rIndex2 udskiftet med summen af rækker rIndex1 og rIndex2.

rowDim()

Katalog >

rowDim(Matrix) ⇒ udtryk

Returnerer antallet af rækker i Matrix.

Bemærk: Se også colDim(), her.

rowNorm()

Katalog >

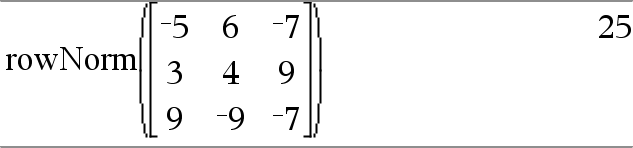
rowNorm(Matrix) ⇒ udtryk

Returnerer maksimum for summerne af de absolutte værdier for elementerne i Matrix-rækkerne.

Bemærk: Alle matricens elementer skal kunne reduceres til tal. Se også colNorm(), her.

rowSwap()

Katalog >

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ matrix

Returnerer Matrix1 med rækkerne rIndex1 og rIndex2 byttet.

rref()

Katalog >

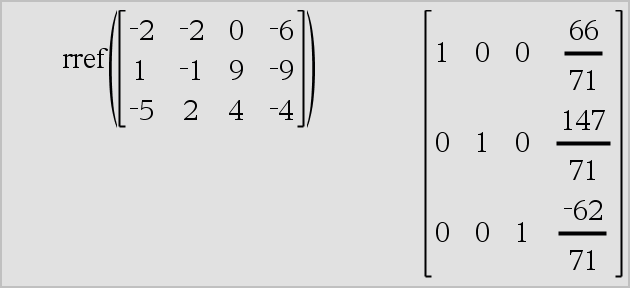
rref(Matrix1[, Tol]) ⇒ matrix

Returnerer den reducerede række-echelonform af Matrix1.

Ethvert element af matricen kan valgfrit behandles som nul, hvis dets absolutte værdi er mindre end Tol. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers ignoreres Tol.

• Hvis du anvender / eller indstiller Auto- eller Approximate -tilstanden til Approximate, foretages beregningerne med flydende komma.
• Hvis Tol udelades eller ikke anvendes, beregnes standardtolerancen som:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Bemærk: Se også ref(), here.