Curves described using polar coordinates can be very interesting and the equations are often much simpler in polar form than they are in rectangular form. This lesson explores graphing polar equations.

When graphing polar functions on the TI-89, is the independent variable and r is the dependent variable. Angles are positive if measured in the counterclockwise direction from the positive x-axis. The independent variable in Polar Graph mode is .

Viewed as function variables, the order of the polar coordinates (r, ) is reversed compared to rectangular coordinates (x, y) where the independent variable is first.

Graphing in Polar Mode

Change to Polar graphing mode on your TI-89.

• Open the Graph Mode menu then highlight "3:POLAR"

• Select and save this mode by pressing twice

Graph the polar function r = 3 sin(2 ).

• Open the Y=Editor by pressing
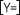
• Set r1 = 3sin(2 )

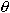is the green feature above .

• Enter the following window values

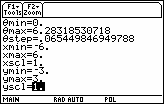
	xmin = –6	ymin = –3
	xmax = 6	ymax = 3
	xscl = 1	yscl = 1

• Display the graph

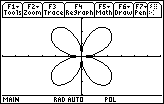
This graph is called a four-leafed rose.

25.2.1 Predict the shape of the graph of r = 3sin(3 ) then verify your prediction by displaying the graph on your TI-89. Click here to check your answer.

Finding the Number of Leaves

There is a relationship between the value of n in the polar function r = 3sin(n ) and the number of leaves.

25.2.2 Determine how n relates to the number of leaves in the graph of r = 3sin(n ) by graphing the following polar functions. You will need to adjust to 2 for the functions where n is even. You may also want to make smaller for the last few functions in order to make the graphs smooth.

r = 3sin(4 )
r = 3sin(5 )
r = 3sin(6 )
r = 3sin(7 )

Click here for the answer.

25.2.3 How many leaves would you expect in the graph of ? Let and graph the function to verify your prediction. Click here for the answer.

Graphing a Cardioid

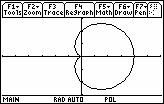
Graph the cardioid r = 2(1 + cos ) using the following viewing window.

Finding a Tangent Line

Use the Tangent feature to find the equation of the line tangent to the cardioid at

• Open the Graph Math menu by pressing
• Highlight "A:Tangent"

• Select this feature by pressing
• Enter /4 for the prompt "Tangent at?"

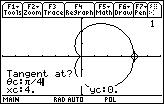
• Press

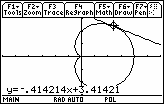
The equation of the tangent line at is approximately y = -0.414x + 3.414, which is given in xy-coordinates and shown at the bottom of the screen.

Finding Arc Length

Find the arc length of the cardioid r = 2(1 + cos ) for .

• Regraph the cardioid by pressing
• Open the Graph Math menu by pressing
• Highlight "B:Arc"

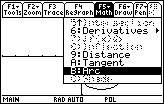
• Press
• Enter 0 for the first point

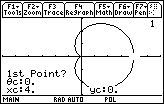
• Enter 2 for the second point

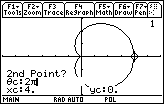
• Press

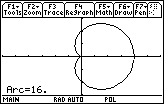
The arc length over the interval is 16 units.