Polar coordinates are an alternative way of identifying points in a plane. They are useful in many applications and for certain types of regions and curves because functions given in polar coordinates can be simple to use. Polar coordinates will be explored in this lesson and you will learn how to convert points given in rectangular coordinates to polar coordinates and vice-versa.
Defining Polar Coordinates
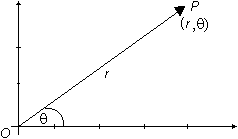
When assigning rectangular coordinates (x, y) to a point P in the plane, x is the horizontal distance and y is the vertical distance from the origin O to the point P.
If polar coordinates (r,
) are used instead, r is the directed distance from the origin O to the point P and
is the directed angle from the positive x-axis to ray OP. Recall that polar coordinates are not unique. In fact, there are infinitely many possible polar coordinates for any point in the plane.
Converting Rectangular Coordinates to Polar Coordinates
The TI-89 has features that convert coordinates from rectangular to polar and vise-versa.
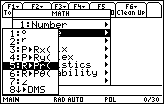
Use the TI-89 to find a value of r for the point (3, 2).
- Set Angle mode to RADIAN
-
Open the Math menu by pressing
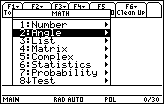
- Highlight "2:Angle"
-
Open the Angle submenu by pressing
-
Highlight "
("
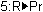This item returns the value of r in one of the possible polar coordinates for a point given in rectangular coordinates.
-
Paste
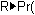to the Edit Line
-
Enter
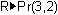
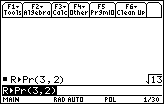
The distance from the origin O to the point P is
, so the polar coordinate r is
.
Find a value of
for this point.
-
Open the Math Angle menu and highlight "
("
-
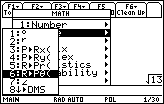
Press
to paste this command to the Edit Line
-
Complete the command
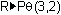and press
-
Display a decimal approximation by pressing
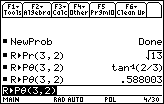
The rectangular point (3, 2) is represented as (
, arctan (2/3)), or approximately as (3.61, 0.588) in polar coordinates. Because the calculator is in Radian mode, the angle is given in radians.
25.1.1 If (r,
) are polar coordinates for a point P, what are the other possible polar coordinates for P? Click here for the answer.
Converting from Polar to Rectangular Coordinates
25.1.2 Use the
and
features in the Math Angle menu to find the x- and y-coordinates for the polar point
. Click here for the answer.
The rectangular coordinates for a point are unique.