The arc length of a segment of a curve was found in Module 17. This lesson will investigate finding the arc length of a parametric curve by using a function that you will define and by using the "Arc" feature in the Math menu of the Parametric Graph screen.

Finding Arc Length of a Parametric Curve

The length of a parametric curve between t = t1 and t = t2 is given by the definite integral

Defining a Function to Compute Arc Length

Because you probably do not want to enter the complicated integral each time, an arc length function can be defined and used for parametric curves defined by x(t) and y(t).

• Define

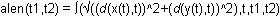
Using the alen Function

Use the alen function to find the length of the parametric curve below for

x = cos³(t)

y = sin³(t)

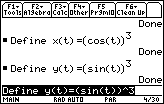
Define the parametric equations.

• Define x(t) = (cos(t))^3
• Define y(t) = (sin(t))^3

• Enter alen(0, /2)

23.3.1 What is the arc length for ?

Click here for the answer.

Finding Arc Length Using a Graph

The length of an arc of a parametric curve can also be found by using the "Arc" feature of the Math menu on the Graph screen. Because x(t) and y(t) are already defined they can be used to graph the parametric curve.

• Set xt1 = x(t)
• Set yt1 = y(t)

If xt1 and yt1 are not selected for graphing, use to select them.

• Graph the curve in a [0, 2 ] x [-3, 3] x [-2, 2] window

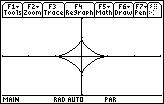
The graph is called a hypocycloid.

The "Arc" feature in the F5:Math menu can now be used to find the arc length.

• Open the Math menu by pressing
• Scroll down to highlight B:Arc

• Activate this feature by pressing
• Enter 0 for the first point
• Enter /2 for the second point

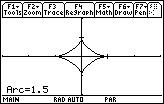
The answer matches the result found with the alen function.

Finding the Length of the Spiral of Archimedes

The spiral of Archimedes is defined by the parametric equations

x = t cos(t)

y = t sin(t)

Find the length of the spiral for 0 t 20.

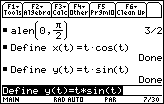
• Define x(t)=t*cos(t)
• Define y(t)=t*sin(t)

Evaluate the arc length between t = 0 and t = 20 by using the alen function.

• Enter alen(0,20)

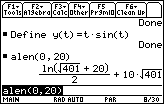
The approximate value is 202.095 units. The result is difficult to obtain with pencil and paper.

Visualizing the Spiral of Archimedes

• Graph the spiral in a [0, 20] x [-30, 30] x [-30, 30] window
• Find the length of the spiral for 0 t 20 using the "Arc" feature of the Graph screen

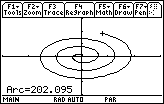
The length of the spiral for 0 t 20 is approximately 202.095 units, which agrees with the value found using the function alen.