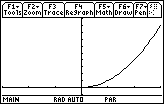
The values of t are restricted to nonnegative values and because x = t the values of x are also restricted to those values.

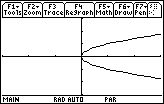
[0, 2 ] x [-4, 4] x [-2, 2]

The first interval given in the window coordinates above represents t-values, the second and third intervals represent x and y-values, respectively.

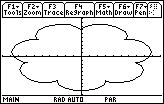
x = 7sin t - sin 7t y = 7cos t - cos 7t	x = 8sin t - sin 8t y = 8cos t - cos 8t

The number of petals is N - 1 in the epicycloid

x = N sin t - sin N t

y = N cos t - cos N t

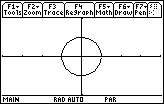
The window shown is [- , ] x [-3, 3] x [-5, 5].

The equation of the tangent to the curve when t = 2 is y 0.642093x + 0.715815.