This lesson investigates the procedure to find derivatives, such as and , for parametric equations x = f(t), y = g(t).

The Chain Rule

Suppose a curve is defined by the parametric equations

x = f(t)

y = g(t)

The Chain Rule states that the derivative on the parametric curve is the ratio of to . Higher derivatives are found in a similar fashion. Symbolically,

Finding First and Second Derivatives

The procedure below will create two functions that return the values of and for parametric equations defined by x(t) and y(t). You can then define x(t) and y(t) and use the new functions to find these two derivatives for the resulting parametric curve.

d vs. d The italicized d's on the right side of each expression below stand for the TI-89 derivative feature, which is accessed by pressing . The other d's represent the letter "d", which is accessed by pressing .

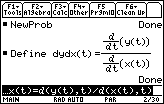
• Perform NewProb
• Define dydx(t) = d(y(t),t)/d(x(t),t)
• Define d2ydx2(t) = d(dydx(t),t)/d(x(t),t)

 

Use the new functions to find dy/dx and d²y/dx² for the parametric equations

x(t) = sec t

y(t) = tan t

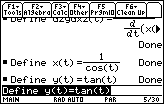
Define the parametric equations below. Recall that sec

• Define x(t)=1/cos(t)
• Define y(t)=tan(t)

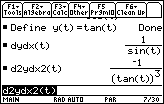
Find and by using the functions defined earlier.

• Enter dydx(t)
• Enter d2ydx2(t)

Finding Derivatives from a Graph

The slope of the tangent line at a point on the graph of a parametric curve can be found by using the "Derivative" feature of the Math menu on the Graph screen.

• Set xt1 = x(t)
• Set yt1 = y(t)
• Set the Window values to [0, 2 ] x [-3, 3] x [-5, 5] and let tstep = 0.1

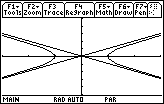
The graph is a hyperbola and the diagonal lines are not a part of the graph. The two diagonal lines are similar to the vertical lines that often appear in graphs of functions that have vertical asymptotes.

Using Dot Style If you graph the parametric equations using "Dot" graphing style the lines will not be displayed. When you graph using "Dot" style you may want to make the value of tstep smaller to increase the resolution of the graph but smaller values of tstep also increase the time required to graph the curve.

• Set tstep to 0.01 and redraw the graph in Dot graphing style.

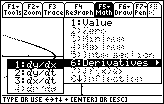
You can use the "Derivatives" feature in the F5:Math menu on the Graph screen to find the value of at t = 0.5.

• Open the Math menu by pressing
• Open the "Derivatives" submenu by pressing

• With "1:dy/dx" highlighted, press to activate this feature
• Enter the value 0.5 and press

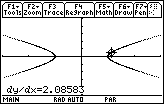
23.2.1 Find the value of at t = 0.5 by entering dydx(0.5) in the Edit Line of the Home screen and compare it to the value found using the "Derivative" feature of the Graph screen. Click here for the answer.

Finding the Equation of the Tangent Line

• Open the F5:Math menu on the Graph screen again by pressing
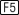
• Scroll down to highlight "A:Tangent".

• Select this feature by pressing
• Enter 0.5 and press

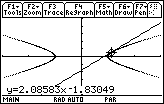
The tangent to the curve at the point when t = 0.5 is drawn and the equation of the tangent line is shown at the bottom of the screen.

23.2.2 Find the slope of the tangent line when t = 2 for the parametric equations

.

Redefining Functions The function to evaluate is already defined. Just redefine x(t) and y(t) and enter the command dydx(2).

Click here for the answer.

23.2.3 Display the curve

Click here for the answer.