In Module 18 you learned how to use the deSolve command and the TI-89 Differential Equation graphing mode to solve first-order differential equations. In this lesson you will learn to use these tools to solve second-order differential equations.

Defining a Second-Order Differential Equation

A second-order differential equation contains a second derivative. If y is the height above ground of a falling object then the first-order derivative y' is the object's velocity and the second derivative y" is its acceleration. The equation y" = k is a second-order differential equation that represents the movement of an object that has constant acceleration k. Initial-value problems that involve a second-order differential equation have two initial conditions.

Solving Second-Order Differential Equations

Suppose that an object is dropped from a height of 48 feet. Because it is dropped without thrust, the initial velocity is zero. The only force acting on the object is gravity, which accelerates it downward 32 feet per second each second.

The height of the object is given by the solution to the second-order differential equation y" = – 32 with initial conditions y(0) = 48 feet and y'(0) = 0 feet per second.

Solve the second-order differential equation to find the equation for the height of the object.

• Perform NewProb
• Enter deSolve(y"= -32 and y'(0)=0 and y(0)=48,t,y)

Enter '' by pressing twice.

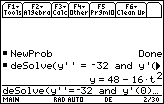
The height of the object is given by y = 48 – 16 t² .

Determine the object's height above the ground at t = 1.3 seconds after it was dropped.

• Paste the expression for y from the History Area to the Edit Line then append "| t = 1.3"

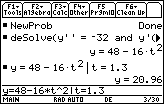
The height of the object at t = 1.3 is 20.96 feet.

20.3.1 Find the height of the object at t = 1.7 seconds.
Click here for the answer.

Only first-order differential equations can be entered in the Y= Editor in Differential Equation graphing mode. However, by making a few substitutions you can still use that mode to solve a second-order differential equation.

Let y1 represent the height of an object. If we let y₂ = y₁', then y₂ represents the velocity of the object and y₂' = y₁" represents its acceleration. The initial height is 48 ft and the initial velocity is 0 ft/s.

• Enter the values shown below in the Y= Editor

• Enter the following window values:

t0 = 0	xmin = 0	ymin = -100	ncurves = 0
tmax = 2	xmax = 2	ymax = 50	Estep = 1
tstep = 0.1	xscl = 0.1	yscl = 10
tplot = 0

Estep Estep, which is used only when the solution method is set to Euler, represents Euler iterations between tstep values. For more accuracy, you can increase Estep without plotting additional points.

• Display the graph of the solution

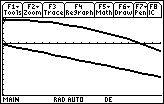
20.3.2 One of the graphs is height and the other is velocity. Which is which?
Click here for the answer.

20.3.3 Approximate the velocity of the object just before it hits the ground by tracing on the height curve to the x-intercept then pressing to jump to the velocity graph.
Click here for the answer.

The Trace cursor was not able to land directly on the x-intercept in this viewing window. At t = 1.7 sec, y was 4.48. At t = 1.8 sec, y was -0.96. To get closer to the actual x-intercept, make the value of tstep smaller in the Window Editor then Trace again.