In this lesson Euler's method is used to approximate a numerical solution to an initial-value problem. The method is based on linear approximations and uses a variation of the point-slope form of a linear equation: y₁ = y₀ + m(x₁ – x₀).

Getting Linear Approximations

Suppose we want to solve a differential equation of the form dy / dx = m(x, y). In general, this means that the slope of the solution y = f(x) at any point (x, y) may depend on both x and y. We are going to approximate the values of the solution at a sequence of x-values given by x₁, x₂, x₃, ..., etc. Given an initial value y₀ = f(x₀), the value of y₁ = f(x₁) can be estimated by the linear approximation.

f(x₁) f(x₀) + m(x₀, y₀) · (x₁ – x₀)

Then the value of y₂ = f(x₂) can be approximated from the value of y₁ = f(x₁).

f(x₂) f(x₁) + m(x₁, y₁) · (x₂ – x₁)

After approximating f(x₂) the same method can be used to approximate f(x₃).

f(x₃) f(x₂) + m(x₂, y₂) · (x₃ – x₂)

Euler's method states that f(x_n+1) can be approximated by using previously found values.

f(x_n+1) f(x_n) + m(x_n, y_n) · (x_n+1 – x_n)

Euler's method generally gives more accurate results if xn+1 – xn is small. In other words, xn+1 is close to xn. In most problems solved with Euler's method, xn+1 – xn is the same for all values of n.

Using Euler's Method

In Lesson 20.1 you solved the logistic initial-value problem

y' = 0.037 * y * (25 – y) and y(1) = 1

Use Euler's method to approximate the values of the solution to this differential equation. Let x₀ = 1, y₀ = 1, and x₁ = 1.1. We compute m(x₀, y₀) = m(1, 1) using the differential equation with y replaced by y₀ = 1.

m(x₀, y₀) = m(1, 1) = 0.037 * 1 * (25-1)

Note that x₁ - x₀ = 0.1, so

y₁ = f(x₁) = f(1.1) f(x₀) + m(x₀, y₀) · (x₁ - x₀)
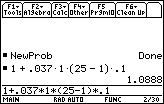
= 1 + 0.037 * 1 * (25-1) * 0.1.

• Perform NewProb
• Enter 1 + 0.037*1*(25 - 1)*0.1

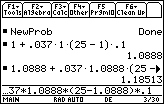
Let x₂ = 1.3, x₃ = 1.2, etc. Next we approximate y₂ = f(1.2) using the approximate value found for y₁ as the value of m(x₁, y₁).

y(1.2) 1.0888 + 0.037 · 1.0888 · (25 – 1.0888) · 0.1

Then continue the process to find y₃, y₄, etc.

Using a Short Cut

There is a short cut that will speed up the process for subsequent approximations. The result of the most recent calculation is stored in a variable called "ans(1)". This can be entered into the Edit Line by pressing . is above . This approach will also improve the accuracy somewhat, since it uses all 14 places, rather than the 6 we entered by hand.

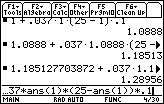
Because the most recent result represents y(1.2), the approximation for y(1.3) can be found by evaluating

y(1.3) ans(1) + 0.037 · ans(1) · (25 – ans(1))· 0.1

• Enter the right-hand side of the expression

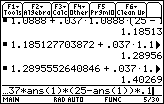
Because ans(1) has now been updated to 1.28956, you can simply press to approximate
y(1.4).

• Approximate y(1.5) by pressing again

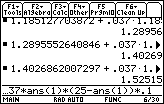
20.2.1 Approximate y(2) by pressing five more times.
Click here for the answer.

The "ans(1)" feature worked well in this example because the given derivative depends only on y. If the derivative is a function of x, the reader will need to edit the command line to change all occurances of the x -value before pressing

Using Euler's Method in Differential Equation Graphing Mode

Euler's method can be used in Differential Equation graphing mode.

• Return to Differential Equation graphing mode
• Open the Y= Editor

The differential equation y' = 0.037.y.(25 – y) with y(1) = 1 should be there.

• Open the GRAPH FORMATS dialog box by pressing and selecting 9:Format
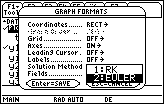
• Move the cursor down to the line labeled "Solution Method"

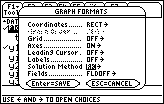
• Highlight "Euler" by pressing

• Select "Euler" for the solution method by pressing
• Save this selection and exit the GRAPH FORMATS dialog by pressing
• Turn on the scatter plot of the data given in Lesson 20.1 and display the new curve by pressing . Check the WINDOW settings to be sure that tstep = 0.1 and Estep (Euler step) = 1.
• Select the Trace feature by pressing
• Select the curve by pressing

A small "1" should appear in the upper right corner of the screen.

Identifying Graphs and Plots When multiple graphs or plots are defined in the Y= Editor and the Trace feature is active, a small number is shown in the upper right-hand corner of the Graph window to identify which graph is selected. Plots are denoted by a prefix of "P." You can change which graph or plot is selected by pressing or .

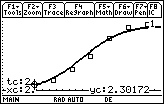
• Display the coordinates of the points on the curve by repeatedly pressing

You should see the same values for y that you calculated with Euler's method.

• Continue to press until the x-coordinate is 2

The same value found for y(2) using Euler's method in 20.2.1 is shown as the y-coordinate.

Displaying a Table of Values

You can see the Euler method values in a table.

• Open the Table Setup dialog box by pressing
• Type 1 for tblStart and 0.1 for tbl

• Save these values by pressing twice
• Display the table by pressing [TABLE]
• Scroll down the table by pressing

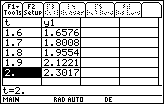
The values shown in the y1 column are found by using Euler's method, which should give you a better understanding of how the TI-89 Differential Equation graphing mode approximates the graph of the solution to an initial-value problem. The calculator computes approximate solution values for very small t-value iterations and displays short line segments that approximate the curve of the solution.

The Runga-Kutta Method The default solution method in Differential Equation Graphing mode is RK, which stands for Runga-Kutta. RK is a solution method that in most cases yields more accurate results than Euler's method but it is more complicated to compute.