In Module 20 you used EULERG and EULERT to solve first-order differential equations. In this lesson you will learn to use another program called DIFF2G to solve second-order differential equations.

Defining a Second-Order Differential Equation

A second-order differential equation contains a second derivative. For example, if y is the height above ground of a falling object then the first-order derivative y ' is the object's velocity and the second derivative y " is its acceleration. The equation y " = k is a second-order differential equation that represents the movement of an object that has constant acceleration k. Initial-value problems that involve a second-order differential equation have two initial conditions.

Solving Elementary Second-Order Differential Equations

Suppose that an object is dropped from a height of 48 feet. Because it is dropped without thrust, the initial velocity is zero. The only force acting on the object is gravity, which accelerates it downward 32 feet per second squared. If y is the height of the object above the ground at time t, then y ' is the velocity of the object and y " is its acceleration.

The equation for the height of the object can be found by solving two first order differential equations.

Because acceleration is the derivative of velocity, the second-order differential equation for acceleration, y " = a = -32, can be rewritten as a first-order differential equation.

1. Solve this differential equation for velocity.
v = –32t + C
2. Solve for C by substituting the initial condition for velocity.

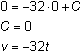
Because velocity is the derivative of height, the equation for velocity v = –32t can be rewritten as a first order differential equation.

1. Solve this differential equation for y, the height.
y = -16t² + C
2. Use the initial condition to find C.

48 = -16 · 0 + C

C = 48

The height of the object at time t is given by y = -16t² + 48.

Using The Solution

The object's height above the ground at t = 1.3 seconds after it was dropped can be found by substituting t = 1.3 in y = -16t² + 48. So the height of the object at t = 1.3 is 20.96 feet.

Graphical and Numerical Solution

The program DIFF2G can be used to find visual and numerical solutions to second-order differential equations without finding the analytic solution. The program takes a second-order differential equation like y " = h(x) and two initial conditions and produces graphs and tables-of-values for both y ' = g(x) and y = f(x).

Downloading the Program to Your Computer

• Click here to download DIFF2G to your computer.
• Choose to save the file.
• Save the file on your local hard disk in a folder that you can access later.

Transferring the Program to the TI-83

Click here to get information about how to obtain the needed cable and review the procedure to transfer the program from your computer to your calculator.

• Send the DIFF2G program from your computer to your TI-83

Using DIFF2G

DIFF2G can be used to solve y " = – 32 with initial conditions y(0) = 48 and y '(0) = 0.

• Clear the Y= editor and turn off the scatter plots.
• Enter the second-order derivative in Y₁. In this situation, Y₁ = -32.

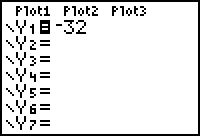
• Define a [0, 2, 0.1] x [-100, 50, 10] viewing window.

• Run DIFF2G
• Enter 0 for INITIAL X    (Initial time is 0.)
• Enter 48 for Y(INITIAL X)    (Initial height is y(0) = 48.)
• Enter 0 for Y '(INITIAL X)    (Initial velocity is y '(0) = 0.)
• Enter 0.01 for the step size    (The difference between sequential time values used to generate a solution.)

After entering the step size, the program will take a few minutes to calculate the solution. When the calculations are complete you should see two graphs.

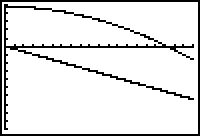
22.3.1 One of the graphs is height and the other is velocity. Which is which? Click here for the answer.

The graph can be used to approximate the height at t = 1.3.

• Trace on the height graph to t = 1.3 (X=1.3). Hold down the key to speed the process.

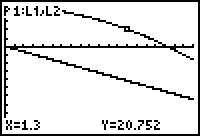
DIFF2G gives an approximation for y(1.3) of 20.752 feet. This is fairly close to the exact value of 20.96 feet found earlier in this lesson.

If the Window settings are changed, the solution can be replotted without running the program again because the solution values are stored in lists L1, L2, and L3. If the window settings are changed and the program is not run again, only the part of the solution corresponding to the x-values that would fit in the original window will be plotted.

22.3.2 Approximate the velocity of the object just before it hits the ground by tracing on the height curve to the x-intercept then pressing to jump to the velocity graph. Look at the table generated by DIFF2G to support the values found by tracing. Click here for the answer.

The Trace cursor was not able to land directly on the x-intercept in this viewing window. At t = 1.72 sec, y = 0.3904. At t = 1.73 sec, y = -0.1632. Use the closer of the two, t = 1.73 sec.