In this lesson Euler's method is used to approximate the solution to an initial-value problem. The method is based on linear approximations and uses a variation of the point-slope form of a linear equation: y₁ = y₀ + m(x₁ – x₀).

Linear Approximations

Suppose we want to solve a differential equation of the form where m(x, y) represents the slope of the function y = f(x) at the point (x, y). In general, this means that the slope of the graph of y = f(x) at any point (x, y) may depend on both x and y.

Euler's Method

Euler's method, which is described below, approximates the y-values of the solution for a sequence of x-values given by x₁, x₂, x₃, ..., etc. The method uses linear approximation to move from one point on the solution curve to the next. At each point, it uses the equation to compute the slope of the tangent line and then moves along the tangent line to the next point.

Basically, since (rise) = (slope) · (run), starting at (x₀, y₀) and moving along the tangent line to the point x = x₁ changes the y-value by m(x₀, y₀) · (x₁ - x₀). The value of y₁ = f(x₁) can therefore be estimated from y₀ = f(x₀) by the linear approximation

f(x₁) f(x₀) + m(x₀, y₀) · (x₁ – x₀).

The next value may be found by repeating the process. The value of y₂ = f(x₂) can be estimated from the value of y₁ = f(x₁) by the linear approximation

f(x₂) f(x₁) + m(x₁, y₁) · (x₂ – x₁).

After approximating f(x₂) the same method can be used to approximate f(x₃).

f(x₃) f(x₂) + m(x₂, y₂) · (x₃ – x₂).

The value of f(x_n+1) can be approximated by using previously found values.

f(x_n+1) f(x_n) + m(x_n, y_n) · (x_n+1 – x_n)

Euler's method generally gives more accurate results if xn+1 – xn is small. In other words, xn+1 is close to xn and the step size is small. In most problems solved with Euler's method, xn+1 – xn is the same for all values of n.

Using Euler's Method

In Lesson 22.1 you graphed an approximate solution to the logistic initial-value problem

Euler's method may be used to approximate the values of the solution to this differential equation. For this problem m(x,y) = 0.037 · y · (25 - y). First let x₀ = 1, y₀ = 1, and x₁ = 1.1, then compute y' = m(x₀, y₀) = m(1, 1), the slope of the graph at (1, 1). Use the differential equation shown above with y replaced by y₀ = 1.

Next, find f(x₁) using the linear approximation equation. Notice that x₁ - x₀ = 0.1

f(x₁) = f(1.1) f(x₀) + m(x₀, y₀) · (x₁ - x₀)
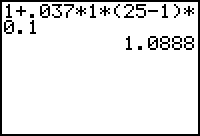
= 1 + 0.888 · 0.1
= 1.0888

You can use the expression for m(x₀, y₀) in the linear approximation equation to find the value of y directly. Using one expression to find y-values will make the computation easier when finding subsequent values.

• Enter 1 + 0.037 · 1 · (25 - 1) · 0.1

Approximate y₂ = f(1.2) using the estimated value found for y₁ and the value of m(x₁, y₁).

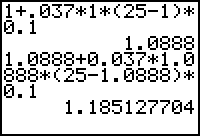
y(1.2) = y₂ = f(x₂) 1.0888 + m(1.1, 1.0888) · 0.1

= 1.0888 + [0.037 · 1.0888 · (25 - 1.0888)] · 0.1

Then continue the process by letting x₃ = 1.3, x₄ = 1.4, ... to find y₃, y₄, ....

The ANS Feature

There is a short cut that will speed up the process for subsequent approximations. The result of the most recent calculation is stored in a variable called ANS which can be entered into a calculation by pressing [ANS]. [ANS] is above . This approach will also improve the accuracy somewhat, since it uses all 14 places, rather than the 4 we entered by hand.

Because the most recent result represents y(1.2), the approximation for y(1.3) can be found by evaluating

y(1.3) Ans + 0.037 · Ans · (25 – Ans)· 0.1

• Enter the right-hand side of this equation on the Home screen and press .

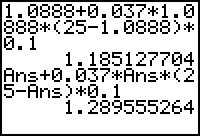
Ans has now been updated to 1.28956.

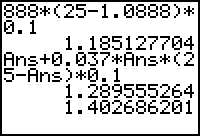
• Simply press to approximate y(1.4).

Pressing re-executes the previous command using the new value stored in ANS and displays the result. When the result is displayed, ANS is updated for the next computation.

• Approximate y(1.5) by pressing again.

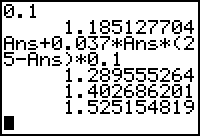
22.2.1 Approximate y(2) by pressing five more times.
Click here for the answer.

The ANS feature works well in this example because y' depends only on y. If y' depends on x, then all occurrences of the x-value in the command line must be changed before is pressed.

Using Euler's Method in TI-83 Programs

Euler's method is used in the EULERG and EULERT programs. EULERG produces a visual solution to the differential equation stored in Y1. In Lesson 22.1, the solution to the logistic differential equation y' = 0.037y(25 - y) that modeled the rumor data was displayed.

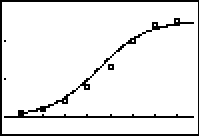
Displaying a Table of Values

You can see the Euler method values with the program EULERT using the same differential equation.

• Set Y₁ = 0.037 · Y · (25 - Y).
• If needed, click here to download EULERT to your computer and then reinstall it on your calculator.
• Run EULERT.
• Enter 1 for the initial values of X and Y.
• Enter 0.1 for the step size.
• Enter 10 for the number of points.

Each time you press you see the coordinates for another point. These are the same values produced by Euler's method using the ANS feature earlier in this lesson.

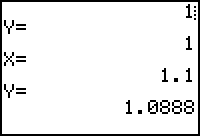
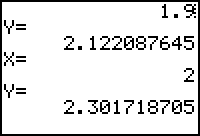
First 2 points with Euler's method	Last 2 points with Euler's method

EULERG also uses Euler's method to calculate x and y coordinates; however, EULERG plots the points instead of displaying the coordinates.