In this lesson you will download a TI-83 program called SLOPEFLD. This program is used to graph slope fields, which can be used to illustrate the general solution of a differential equation.

Downloading the Program to Your Computer

• Click here to download SLOPEFLD to your computer.
• Choose to save the file.
• Save the file on your local hard disk in a folder that you can access later.

Transferring the Program to the TI-83

If necessary, click here to get information about how to obtain the needed cable and review the procedure to transfer the program from your computer to your calculator.

• Send the SLOPEFLD program from your computer to your TI-83.

Solving Differential Equations using Slope Fields

The program SLOPEFLD may be used to solve differential equations. Like EULERG the function must be entered into Y1 in the Y= editor and a viewing window must be defined.

Display the slope field associated with y' = 2x using SLOPEFLD by following the procedure below.

• Enter Y₁ = 2X.
• Select a [-2, 2, 1] x [-4, 4, 1] viewing window.
• Run program SLOPEFLD.

The slope field contains short line segments with slope 2x at selected points in the window. This particular window uses 100 points arranged in 10 rows and 10 columns. The line segments could be thought of as linear approximations, or tangent lines, of particular solutions through the points.

Notice that all the line segments in a given column are parallel because they all have the same x-coordinate and therefore the same slope, 2x.

Graphing a Particular Solution with a Slope Field

You can graph the particular solution to the differential equation y' = 2x that satisfies the initial condition y(0) = 1. In Lesson 20.2 we saw the solution to this initial value problem is y = x² + 1.

• Enter Y₂ = X² + 1.
• Select the thick graphing style for Y₂.
• Y₁ should still be unselected.

• Press to see the particular solution together with the slope field.

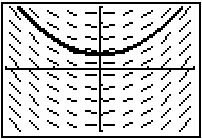
In the graph above, the slope field is shown again, and the particular solution when y(0) = 1 is indicated by the darker connected curve.

Changing Initial Conditions

Graph the particular solution to the differential equation y' = 2x that satisfies the initial condition

y(0) = -1. The solution to this initial-value problem is y = x² - 1

• Enter Y₃ = X² - 1.
• Select the thick graphing style for Y₃.
• Press .

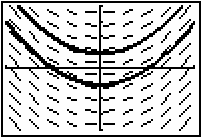
This particular solution is a vertical shift of the previous particular solution. All the particular solutions to the differential equation y' = 2x are vertical shifts of the curve y = x². The general solution to the differential equation y' = 2x is y = x² + C. Different values of C correspond to different particular solutions. The slope field could be thought of as an illustration of all possible particular solutions.

The Slope Field of y' = y

The slope field for the differential equation y' = y is significantly different than the one above. A solution of y' = y represents a function where the slope of the tangent at each point (x, y) is the y-coordinate of that point. The slope of solutions to y' = y is a function of y rather than x. How do you think this will affect the slope field?

20.4.1 Sketch a rough approximation of the slope field for y ' = y. Compare your slope field with the slope field given by the SLOPEFLD program using a [-2, 2, 1] x [-5, 5, 1] window. What is the major difference between the slope field for this problem and the slope field for the previous problem?

Click here for the answer.