One antiderivative appears to be , as confirmed by the graph of Y₂ = X⁴ / 4 coinciding with the graph of .

[-5, 5, 1] x [-15, 15, 5]

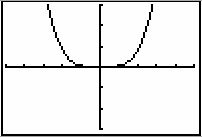Y1 = fnInt(T^3,T,0,X) Y2 = X^4/4

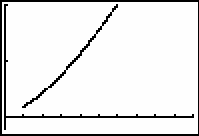
The graph shown is that of , the solution of with y(1) = 1 which was found earlier.

You need 20 points to reach y(1) 1.95.

y(1.2) 1.2073. The actual value rounds to 1.2097.

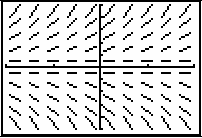
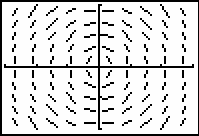
In this slope field the slopes of segments in a given row are equal. In the previous slope field the slopes of segments in a given column were equal. This difference is due to the fact that the differential equation in this problem is a function of y, therefore the slopes depend on y, not x.

Y₁ = fnInt(cos(T/2),T,0,X)

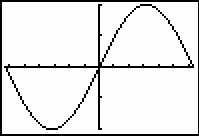
[-2 ,2 ,1] x [-2, 2, 1]

Any integral of the form is a member of the family of curves represented by .
The graph shown above is the graph for a = 0. Other values of a will produce vertical shifts of this graph.