Module 20 - Antiderivatives as Indefinite Integrals and Differential Equations

Module 20 - Antiderivatives as Indefinite Integrals and Differential Equations

Lesson 20.3: Solving Differential Equations Numerically

In this lesson you will use the TI-83 program EULERT to make tables for solutions to initial value problems.

Downloading the Program to Your Computer

Click here to download EULERT to your computer.

Choose to save the file.

Save the file on your local hard disk in a folder that you can access later.

Transferring the Program to the TI-83

If necessary, click here to get information about how to obtain the needed cable and review the procedure to transfer the program from your computer to your calculator.

Send the EULERT program from your computer to your TI-83.

EULERT Entries

The entries for EULERT are similar to EULERG. You enter the differential equation in Y₁. When you run EULERT you will see prompts for the initial values of X and Y as well as the step size. When running EULERT, you also need to enter the number of points to be computed. When EULERT runs, instead of seeing a graph, you will see approximate coordinates of points on the graph of the solution.

Numerical Solutions to Differential Equations

EULERT also uses Euler's method, and therefore only gives approximate numerical solutions.

Find a numerical solution to the initial value problem y' = 2x with the condition that y(0) = 1 by using EULERT.

Clear the Y= editor.
Enter Y1 = 2X.
Run program EULERT.
Enter 0 for the initial value of X.
Enter 1 for the initial value of Y.
Enter 0.1 for the step size.
Enter 10 for the number of points.

After you enter the number of points you should see the coordinates for the initial point. The busy indicator should appear in the upper right-hand corner of the screen.

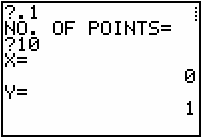
Each time you press you will see another pair of coordinates. These coordinates are approximations of points on the solution curve.

Continue pressing until you see the last point. The program should say "Done."

This result says that the point (1,1.9) lies on the graph of the solution to the initial value problem y' = 2x, y(0) = 1.

Approximate Answers from EULERT

The analytic solution to the initial value problem is y = x² + 1. In the solution when x = 1, y = 2, yet with a step size of 0.1 the program predicted a y-value of 1.9. EULERT uses a numerical method that gives approximate, not exact solutions to initial value problems.

20.3.1 Redo the same problem above with a step size of 0.05 to see which value for y is predicted by the program for x = 1.

Click here for the answer.

Getting Better Results with EULERT

Smaller values for the step size in EULERT will generally give more accurate results. A step size of 0.01 in the previous example would give more accurate results than the value of 0.1 that was used. However, a step size of 0.01 would require the program to compute100 points to move from the initial value of x = 0 to x = 1.

20.3.2 Given and y(1) = 1 use EULERT to estimate y(1.2). Use a step size of 0.05.

Click here for the answer.

< Back | Next >