This lesson introduces the Arc Length Theorem. The theorem is then used to compute the arc length of a curve.

Arc Length Theorem

If a curve y = f(x) has a continuous derivative on the interval [a, b], its arc length is given by

.

Finding Arc Length

The theorem often gives integrals that are difficult or impossible to evaluate by hand. The TI-83 can be very helpful in evaluating or approximating these integrals.

Find the length of the curve y = x^2/3 on the interval [1, 2].

• Enter Y1 =X^(2/3).
• Enter Y2 = nDeriv(Y1,X,X).
  
  

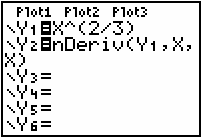
• Evaluate the integral 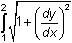by entering 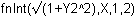on the Home screen.
  

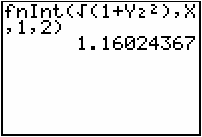
The arc length of the curve is approximately 1.16024 units.

Writing Complicated Formulas Writing the arc length formula with the function in Y1 and the derivative in Y2 makes entering the definite integral on the TI-83 easier than entering the entire formula on the Home screen. However, if we use the symbolic derivative and enter the complete integral on the Home screen (without using the Y= editor), we will generally get a more accurate result.

19.3.1 Find the approximate length of the curve y = x² between x = -1 and x = 2.

Click here for the answer.