In previous modules you used the definite integral to find the area bounded by a function and the x-axis. In each case the graph of the function was above the x-axis. In this lesson you will see what happens when the function dips below the x-axis. You will also investigate the concept of the definite integral as a net-area function.

All the curves explored in Module 18 were above the x-axis. The following investigates a definite integral when part of the curve is below the x-axis.

• Graph y = sinx in a [0, 2 , 1] x [-1, 1, 1] window.

• Evaluate the integral 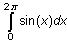by using the integral key.

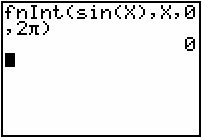
How can the result be zero? The area bounded by y = sin x and the x-axis certainly is not zero. To help answer this question, break the interval of integration into two subintervals that represent the areas above and below the x-axis: [0, ] and [ , 2 ].

• Evaluate 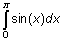and .

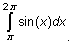Finding Positive and Negative Integrals

Review the graph of y = sin x and the values of the definite integrals and .

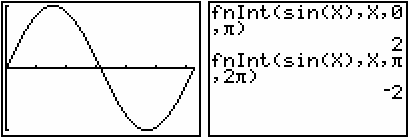
The graph from 0 to is above the x-axis and the corresponding definite integral is positive.

The graph from to 2 is below the x-axis and the corresponding definite integral is negative.

Finding Net Area

The definite integral represents the value of the net area, or the area above the x-axis minus the area below the x-axis. From the above, we know the area above the x-axis is 2 and the area below the x-axis is 2. The net area between the curve y = sinx and the x-axis on this interval is therefore 2 minus 2, or zero.

19.1.1 Use the definite integral feature in the CALC menu of the Graph screen to approximate the values of

Click here for the answer.

Visualizing

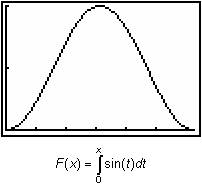
You can obtain the general shape of a corresponding net area function on the interval [0, 2 ] by examining the graph of y = sinx.

• Refresh the graph of y = sin x by pressing    .

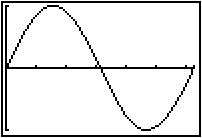
The following characteristics of the net area function can be determined from the graph of the curve y = sinx. Look at the graph while reading the tables below. Recall that the curve function is the derivative of the net area function, or in this case, F ' (x) = sin(x).

x-axis Interval	Curve Function	Area Function
[0, ]	positive	increasing
[ , 2 ]	negative	decreasing
and	increasing	concave upward
	decreasing	concave downward

Furthermore, the x-values where maximums, minimums, and points of inflection occur can be identified by examining how the curve function is changing.

x-value	Curve Function is Changing	Area Function
x =	from positive to negative	local maximum
	from increasing to decreasing	point of inflection
	from decreasing to increasing	point of inflection

Other characteristics of the net area function include:

1. When x = 0, the net area is 0.
2. The net area on the interval [0, ] is 2 and the net area function begins to decrease at that point, so the maximum of the net area function is 2 when x = .
3. The net area on the interval [0, 2 ] is 0, so the net area function is 0 when x = 2 .

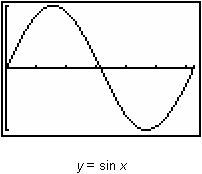
With these characteristics you can draw a graph of the net area function . Using the TI-83 we can graph F(x) and support the above results.

Graph F(x) by following the procedure below.

• Enter Y1 = fnInt(sin(T),T,0.X).
• Display the graph in a [0, 2 , 1] x [0, 2, 1] window.

Visualizing the general shape of the integral function is often very helpful.

Extending the Procedure to Other Curves

19.1.2 Graph the curve and find the net area bounded by y = x³ – 3x² – x + 3 and the x-axis on the interval [0, 4].

Click here for the answer.

Visualizing

The characteristics of the net area function can be found by examining the graph of the curve function. The graph of the curve is shown below in a [0, 4, 1] x [ -5, 15, 1] window with a list of the net area function's characteristics.

When x = 0 the net area function is 0. The net area function is increasing on (0, 1) and (3, 4) because the curve function is positive there. The net area function is decreasing on (1, 3) because the curve function is negative there. The net area function is concave downward on (0, 2.1547) because the curve is decreasing there. The net area function is concave upward on (2.1547, 4) because the curve is increasing there. Because the curve changes from positive to negative at x = 1, the net area function has a local maximum there. Because the curve changes from negative to positive at x = 3, the net area function has a local minimum there. The net area function is positive on the interval (0, 2), because there is more area above the axis than below it. The area from x = 0 to x = 1 appears to be about the same as the area from x = 1 to x = 2, so the net area function is about 0 when x = 2. This can be confirmed by evaluating the integral . From x = 2 to somewhere beyond x = 3 the net area function is negative because more of the area is below the x-axis to that point. Somewhere beyond x = 3 the net area function becomes positive again because more area is above the x-axis than below it.

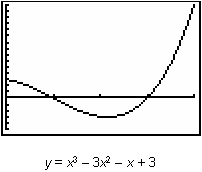
The graphs of the curve function and the net area function are shown below for comparison.

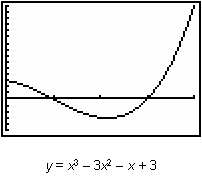
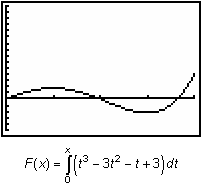
19.1.3 Sketch the graph of the net area function that corresponds to the following curve in the window [0, 4, 1] x [-2, 2, 1].

Click here for the answer.