This lesson explores finding the total area bounded by a curve and the x-axis on a given interval. It also investigates finding the area between two curves.

The total area of a region that is both above and below the x-axis is found by separating the positive parts of the graph from the negative parts. Each part is integrated and the absolute values of the results are added together to find the total area.

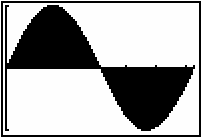
Examine the graph of y = sinx from 0 to 2 again.

As shown in Lesson 19.1, , and .

The total area bounded by y = sinx and the x-axis on the interval [0, 2 ] is 2 + | -2 | = 4 square units.

Using Absolute Value to Find Total Area

Another method used to find the total area is to integrate the absolute value of the function. You can find the absolute value, abs(), by pressing .

Compare the graphs of y = sin(x) and y = |sin(x)| shown below in the [0,2 ] x [-2, 2] window. Notice that the absolute has the effect of reflecting the part of the graph of sin(x) that is below the x-axis so that it is above the x-axis. The integral of |sin(x)| from 0 to 2 gives the total area bounded by the curve y = sin(x) and the x-axis between x = 0 and x = 2 .

Evaluate and interpret the result.

• Clear the Home screen.
• Enter fnInt(abs(sin(X)),X,0,2 ).

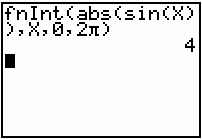
The total area bounded by y = sinx and the x-axis on the interval [0, 2 ] is 4 square units.

19.2.1 Find the total area bounded by y = x³ – 3x² – x + 3 and the x-axis on the interval [0, 4] by integrating the absolute value of y = x³ - 3x² - x + 3. Click here for the answer.

Finding the Area between Two Curves

Integrals can be used to find the area between two curves by evaluating the integral of the value of the upper curve minus the lower curve between their points of intersection. Find the area between y = 4 – x² and y = x by following the procedure below.

• Graph the two functions y = 4 – x² and y = x in a [-3, 3, 1] x [-5, 5, 1] window.

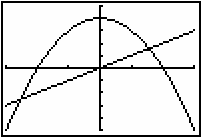
The upper curve is y = 4 – x² and the lower curve is y = x.

Find the points where the curves intersect.

• Select 5:intersect from the CALC menu in the Graph screen.
  

• Select the two curves and move the cursor close to the left point of intersection.
• Press to find the left point of intersection.
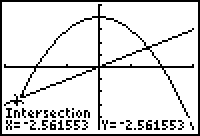
• Repeat this process for the right point of intersection.

19.2.2 What is the approximate x-coordinate of the right point of intersection?
Click here for the answer.

We now need to integrate the upper curve minus the lower curve. The approximate area between the curves is given by

19.2.3 Evaluate the integral above on your TI-83 and interpret the result. Click here for the answer.

Using Stored Values It is often a good idea to carry all decimals from an intermediate computation until you complete the problem. For the above integral you could store all the decimals involved in the left x-coordinate using the following procedure: Finding the intersection on the graph screen. Before doing anything else go to the Home screen by pressing [QUIT]. Then press which contains the x-value shown on the Graph screen. Then press [A], which stores all the decimals in the left x-coordinate approximation to the variable A. Similarly, you could store all the decimals in the right x-coordinate approximation into B. You may then evaluate the integral . The approximations may not appear very different - but they are different, and we would generally expect the one we get by storing the values to be more accurate.